Linee perpendicolari (perpendicolarità) -

In questa pagina troverai tutto sulle rette perpendicolari: cosa sono, quando due rette sono perpendicolari, come calcolare una retta perpendicolare ad un’altra, le sue proprietà,… Inoltre potrai vedere degli esempi e potrai pratica con esercizi risolti passo dopo passo.

Cosa sono due rette perpendicolari?

In matematica, due rette sono perpendicolari quando si intersecano in un punto formando quattro angoli retti uguali (90º).

Inoltre, anche i vettori di direzione di due linee perpendicolari devono essere perpendicolari.

La perpendicolarità di due linee è generalmente indicata dal simbolo

$\perp .$

Ricordiamo invece che nel piano ci sono 4 possibilità nel concetto di posizione relativa tra due linee: due linee possono essere secanti, perpendicolari, coincidenti o parallele. Se lo desideri, puoi verificare il significato di ciascun tipo di riga sul nostro sito.

Come fai a sapere se due rette sono perpendicolari?

Esistono due modi per determinare quando due linee sono perpendicolari, dai loro vettori di direzione o dalle loro pendenze . Di seguito hai la spiegazione di entrambi i metodi, sebbene servano allo stesso scopo, ti consigliamo di sapere come eseguire entrambe le procedure perché ognuna dipende da come sono espresse le linee.

Dai vettori di direzione delle linee

Un modo per sapere quando due linee sono perpendicolari è utilizzare i vettori di direzione delle linee in questione. Ricordiamo che il vettore direzione è quel vettore che indica la direzione di una linea.

Anche i vettori di direzione di due linee perpendicolari sono mutuamente ortogonali. Pertanto, se il prodotto scalare dei vettori di direzione di due linee è uguale a 0, significa che le linee sono perpendicolari.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s =0 \quad \longrightarrow \quad r \perp s$

Vediamo come viene determinata la perpendicolarità di due rette utilizzando un esempio:

$\displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}$

Entrambe le linee sono espresse come equazioni parametriche, quindi i componenti del vettore di direzione di ciascuna linea sono i numeri davanti al parametro

$t:$

$\vv{\text{v}}_r =(-2,3) \qquad \qquad \vv{\text{v}}_s=(3,2)$

Una volta conosciuto il vettore direzione di ciascuna linea, controlliamo se sono perpendicolari calcolando il prodotto tra i vettori:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-2,3)\cdot (3,2) = -2\cdot 3 +3\cdot 2= \bm{0}$

Il prodotto scalare dei due vettori è zero, quindi le linee sono perpendicolari.

Pendenze della linea

Un altro modo per determinare se due rette sono perpendicolari è usare le loro pendenze. Ricorda che la pendenza di una linea è il coefficiente

$m$

dell’equazione esplicita e dell’equazione punto-pendenza di una retta.

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

E dai coefficienti si può ricavare anche la pendenza di una retta

$A$

$B$

dell’equazione implicita (o generale) di una retta:

$Ax+By+C= 0 \ \longrightarrow \ m = -\cfrac{A}{B}$

Pertanto le pendenze di due rette perpendicolari sono inverse e di segno opposto, cioè è sempre soddisfatta la seguente uguaglianza:

$r \perp s \quad \longrightarrow \quad m_r=-\cfrac{1}{m_s}$

Quindi se il prodotto delle pendenze di due rette diverse è uguale a -1, ciò implica che le rette sono perpendicolari:

$m_r\cdot m_s=-1\quad \longrightarrow \quad r \perp s$

Ad esempio, le due rette seguenti sono perpendicolari:

$r: \ y=2x+4 \qquad \qquad s: \ y=-\cfrac{1}{2} \ x-5$

Possiamo dimostrare che sono due rette perpendicolari tra loro a partire dai loro pendii. La pendenza di ciascuna retta è:

$m_r = 2 \quad \quad m_s=-\cfrac{1}{2}$

Ora moltiplichiamo le pendenze:

$\displaystyle 2 \cdot \left(-\frac{1}{2} \right) = -\cfrac{2}{2} = \bm{-1}$

Il prodotto tra le due pendenze equivale a -1, che in realtà significa due linee perpendicolari tra loro.

Come calcolare una linea perpendicolare ad un’altra?

Anche se può sembrare difficile da fare, trovare una linea perpendicolare ad un’altra è abbastanza semplice, per questo hai solo bisogno di un vettore direzione perpendicolare alla linea e di un punto che appartiene alla linea.

L’unica difficoltà è che, come prima, la procedura dipende dal tipo di equazione in cui sono espresse le rette. Perché una linea perpendicolare ad un’altra può essere calcolata dai vettori di direzione o dalle pendenze .

Dal vettore di direzione di destra

Una linea perpendicolare ad un’altra linea data può essere trovata utilizzando il suo vettore direzione. Vediamo come si fa con un esempio:

Calcola la retta perpendicolare alla retta
$r$

ciò che passa per il punto

$P(5,-1)$

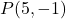
. essere sincero

$r:$

$\displaystyle r : \ 3x+2y-1=0$

La prima cosa che dobbiamo fare è identificare il vettore direzione della retta. In questo caso la retta è definita sotto forma di un’equazione generale (o implicita), pertanto le coordinate cartesiane del vettore direzione della retta possono essere ottenute con i coefficienti A e B della retta:

$\vv{\text{v}}_r =(-B,A)=(-2,3)$

E una volta conosciuto il vettore direzione della linea, dobbiamo calcolare un vettore perpendicolare ad essa. Per fare ciò è sufficiente inserire le coordinate del vettore e cambiare il segno di uno di essi (quello che desideri):

$\vv{\text{v}}_\perp =(3,2)$

Quindi ora conosciamo il vettore direzione della retta. L’equazione implicita della retta sarà quindi la seguente:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}$

$Ax+By+C \ \longrightarrow \ 2x-3y+C=0$

Pertanto è sufficiente determinare il parametro C. Per fare ciò, sostituiamo il punto che appartiene alla retta nella sua equazione e risolviamo l’equazione risultante:

$P(5,-1)$

$2x-3y+C=0 \ \xrightarrow{x=5 \ ; \ y=-1} \ 2\cdot 5-3\cdot (-1)+C=0$

$10+3+C=0$

$13+C=0$

$C=-13$

In conclusione l’equazione della retta perpendicolare è:

$\bm{2x-3y-13=0}$

Dalla pendenza della linea

Un altro modo per trovare una retta perpendicolare ad una certa retta è dalla sua pendenza. Vediamo come si risolve questo tipo di problema attraverso un esempio:

Calcola la retta perpendicolare alla retta
$r$

ciò che passa per il punto

$P(0,1)$

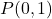
. essere sincero

$r:$

$\displaystyle r : \ y=4x-3$

La pendenza della linea

$r$

Est:

$m_r = 4$

Una volta conosciuta la pendenza della retta, dobbiamo trovare la pendenza della retta perpendicolare. Come abbiamo visto nelle sezioni precedenti, le pendenze di due rette perpendicolari sono inverse e hanno cambiato segno. Pertanto, per determinare la pendenza della retta perpendicolare, occorre invertire la pendenza trovata e cambiarne il segno:

$m_\perp =-\cfrac{1}{4}$

L’equazione esplicita della retta perpendicolare sarà quindi la seguente:

$y= mx+n$

$y=-\cfrac{1}{4} \ x + n$

Infine calcoliamo l’ordinata all’origine della retta perpendicolare sostituendo le coordinate del punto nell’equazione della retta:

$P(0,1)$

$y=-\cfrac{1}{4} \ x + n \ \xrightarrow{x=0 \ ; \ y=1} \ 1 =-\cfrac{1}{4}\cdot 0 + n$

$1 = n$

In breve, l’equazione della retta perpendicolare è:

$\bm{y=-}\mathbf{\cfrac{1}{4}} \ \bm{x + 1}$

Proprietà delle rette perpendicolari

Tutte le linee perpendicolari hanno le seguenti caratteristiche:

Relazione simmetrica : se una linea è perpendicolare ad un’altra linea, anche quella linea è perpendicolare alla prima linea.

$r \bm{\perp} s \ \longrightarrow \ s \bm{\perp} r$

Proprietà non riflessiva : ovviamente nessuna retta può essere perpendicolare a se stessa.

$r \ \cancel{\bm{\perp}}} \ r$

Teorema: Nella geometria euclidea (in R2), qualsiasi coppia di rette perpendicolari ad una terza retta deve necessariamente essere parallela. Cioè, se una linea è perpendicolare ad un’altra linea e quella linea è anche perpendicolare ad una terza linea, la prima e l’ultima linea sono parallele.

Risolti problemi di rette perpendicolari

Esercizio 1

Quale delle seguenti rette è perpendicolare alla retta

$r: y=3x+4$

$a : \ y=3x-\cfrac{1}{3}$

$b : \ y=-\cfrac{1}{3} \ x+5$

$c : \ y=-4x-3$

$d : \ y=\cfrac{1}{3} \ x-5$

$e : \ y=-\cfrac{1}{3} \ x-2$

vedi soluzione

La pendenza della linea

$r$

è 3:

$m_r=3$

E le pendenze di due rette perpendicolari sono inverse e di segno opposto, quindi la pendenza di qualunque retta perpendicolare alla retta

$r$

deve essere:

$m_\perp=-\cfrac{1}{3}$

In modo che le linee siano perpendicolari alla linea

$r$

sono quelli la cui pendenza è uguale a

$-\cfrac{1}{3}$

. Vale a dire, le linee

$\bm{b}$

$\bm{e}.$

Esercizio 2

Determina se le due rette seguenti sono perpendicolari:

$\displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}$

vedi soluzione

la destra

$r$

è espresso sotto forma di un’equazione parametrica, tale che le componenti del vettore direzione di detta linea siano i numeri che precedono il parametro

$t:$

$\vv{\text{v}}_r =(-1,-3)$

D’altra parte, la linea retta

$s$

è definito sotto forma di un’equazione continua, quindi le coordinate del suo vettore direzione sono i numeri dei denominatori:

$\vv{\text{v}}_s =(4,6)$

Una volta conosciuto il vettore direzione di ciascuna linea, possiamo verificare se sono perpendicolari calcolando il prodotto dei due vettori:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-1,-3)\cdot (4,6) = -1\cdot 4 + (-3)\cdot 6= -22 \bm{\neq 0}$

Il prodotto scalare dei due vettori è diverso da zero, quindi le linee non sono perpendicolari .

Esercizio 3

Trova la retta perpendicolare alla retta

$r$

ciò che passa per il punto

$P(-2,1)$

. essere sincero

$r:$

$\displaystyle r : \ 4x-y+5=0$

vedi soluzione

La prima cosa che dobbiamo fare è identificare il vettore direzione della retta. In questo caso la retta è definita sotto forma di equazione generale (o implicita), quindi il suo vettore direzione è:

$\vv{\text{v}}_r =(-B,A)=(1,4)$

Una volta conosciuto il vettore direzione della retta, dobbiamo calcolare un vettore perpendicolare ad essa. Per fare ciò è sufficiente inserire le coordinate del vettore e cambiare il segno di uno di essi (quello che desideri):

$\vv{\text{v}}_\perp =(4,-1)$

L’equazione implicita della retta sarà quindi la seguente:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}$

$Ax+By+C \ \longrightarrow \ -x-4y+C=0$

È quindi sufficiente determinare l’incognita C. Per fare ciò sostituiamo il punto per il quale passa la retta nella sua equazione:

$P(-2,1)$

$-x-4y+C=0 \ \xrightarrow{x=-2 \ ; \ y=1} \ -(-2)-4\cdot 1+C=0$

$2-4+C=0$

$-2+C=0$

$C=2$

Infine l’equazione della retta perpendicolare è:

$\bm{-x-4y+2=0}$

Esercizio 4

Trova l’equazione punto-pendenza della retta perpendicolare alla retta

$r$

ciò che passa per il punto

$P(3,-2)$

. essere sincero

$r:$

$\displaystyle r : \ y=5x+1$

vedi soluzione

La pendenza della linea

$r$

Est:

$m_r = 5$

Una volta conosciuta la pendenza della retta, dobbiamo trovare la pendenza della retta perpendicolare. Per fare ciò è sufficiente invertire la pendenza trovata e cambiarne il segno:

$m_\perp =-\cfrac{1}{5}$

Infine, sostituiamo semplicemente la pendenza trovata e le coordinate del punto nell’equazione punto-pendenza della retta:

$y -y_0=m(x-x_0)$

$y-(-2)=-\cfrac{1}{5} (x- 3)$

$\bm{y+2=}\mathbf{-\cfrac{1}{5}}\bm{ (x- 3)}$

Esercizio 5

la destra

$r$

passa per i punti (2,1) e (4,2), e la retta

$s$

passa per i punti (-1,2) e (1,-2). Determina se si tratta di due linee perpendicolari o meno.

vedi soluzione

Per verificare se si tratta di due rette perpendicolari, calcoleremo le loro pendenze e poi vedremo se rispettano il rapporto perpendicolare. Ricorda che la formula per la pendenza di una retta è:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

La pendenza della linea

$r$

Est:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{2-1}{4-2} = \cfrac{1}{2}$

La pendenza della linea

$s$

Est:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{-2-2}{1-(-1)} = \cfrac{-4}{2}=-2$

Per verificare la perpendicolarità delle due rette, dobbiamo vedere se la pendenza di una retta è l’inverso della pendenza dell’altra. In questo caso le due pendenze sono inverse e hanno anche segno opposto, quindi le due rette sono perpendicolari tra loro.

Esercizio 6

Calcolare il valore di

$k$

in modo che le due rette seguenti siano perpendicolari:

$\displaystyle r: \ 5x+3y-7=0\qquad \qquad s: \ 4x+ky+1=0$

vedi soluzione

Le due rette sono espresse sotto forma di un’equazione implicita (o generale) e il vettore direzione di un’equazione implicita della retta è:

$Ax+By+C=0$

$\vv{\text{v}} =(-B,A)$

Pertanto, il vettore direzione di ciascuna linea sarebbe:

$\vv{\text{v}}_r =(-3,5) \qquad \qquad \vv{\text{v}}_s =(-k,4)$

Affinché due rette siano perpendicolari, il prodotto scalare dei loro vettori di direzione deve essere zero. Pertanto, applicheremo questa condizione per trovare il valore dell’incognita

$k:$