Iperbole: definizione, formula, elementi, equazione, esempi,…

Qui troverai tutto sull’iperbole: cos’è, quali sono i suoi elementi caratteristici, come trovarne l’equazione, esempi, esercizi risolti, ecc.

Cos’è l’iperbole?

L’iperbole è una curva aperta con due rami, la cui definizione matematica è la seguente:

Nella geometria analitica, un’iperbole è il luogo dei punti del piano che soddisfa la seguente condizione: il valore assoluto della differenza delle distanze tra un punto qualsiasi dell’iperbole e due punti fissi (detti fuochi) deve essere costante.

Inoltre, il valore della sottrazione di queste due distanze è sempre equivalente alla distanza tra i due vertici dell’iperbole.

$\lvert d_1 - d_2 \rvert = 2a$

Di seguito vedremo cosa significa il coefficiente

$a$

di un’iperbole.

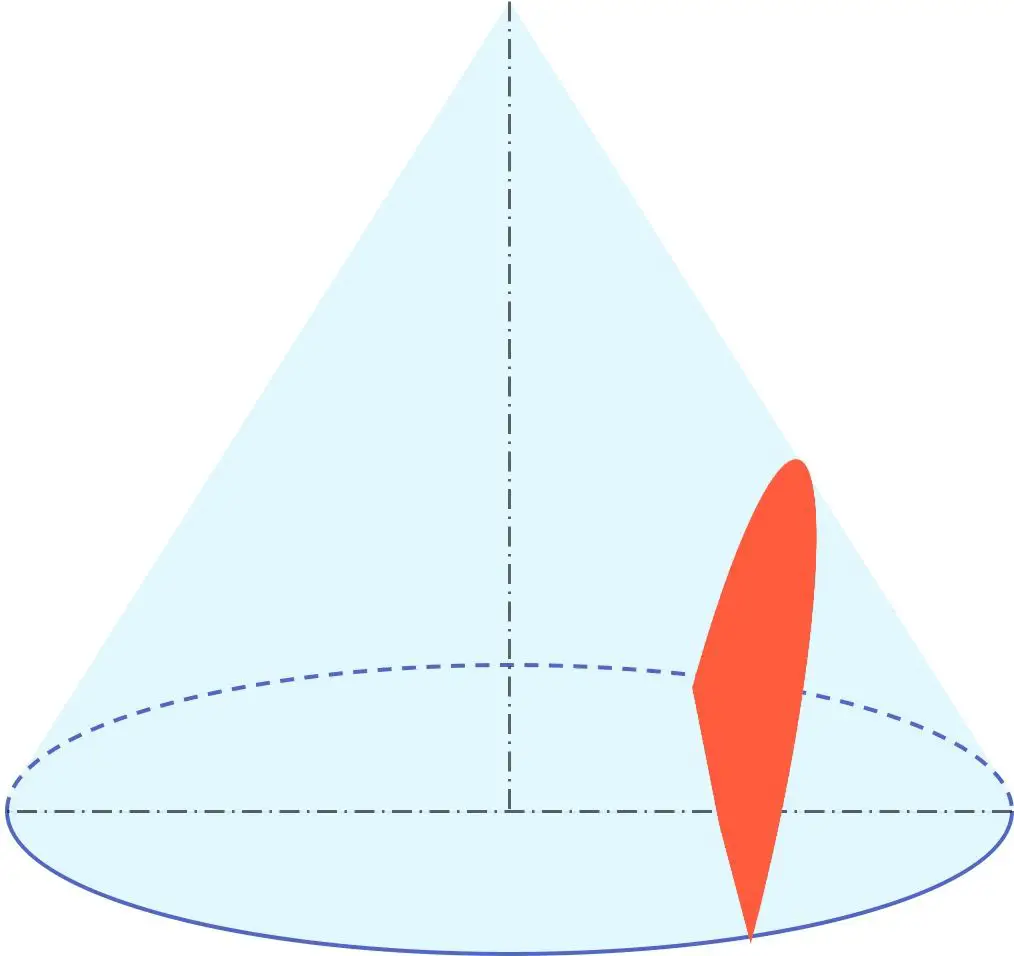
Inoltre l’iperbole fa parte del gruppo geometrico chiamato coniche insieme alla circonferenza, all’ellisse e alla parabola. L’iperbole è quindi una sezione conica, o in altre parole si può ottenere da un cono.

In particolare, un’iperbole è il risultato della sezione di un cono mediante un piano avente un angolo minore dell’angolo formato dalla generatrice del cono rispetto al suo asse di rivoluzione.

Elementi di un’iperbole

Le caratteristiche di un’iperbole dipendono da:

I fuochi : sono due punti fissi caratteristici di ciascuna iperbole (punti F e F’ nel grafico sottostante). Il valore assoluto della differenza tra le distanze da qualsiasi punto dell’iperbole a ciascun fuoco è costante e uguale a
$2a.$
Asse focale o principale : è la retta che passa per i due fuochi dell’iperbole. Corrisponde ad un asse di simmetria di detta figura geometrica. Chiamato anche asse trasversale o trasversale.
Asse secondario : è la bisettrice del segmento FF’ (retta passante per i punti B e B’). Inoltre è una linea perpendicolare all’asse focale ed è un altro asse di simmetria dell’iperbole
Centro (O) : è il punto di intersezione dei due assi e il punto medio dei due vertici e dei due fuochi. Poiché l’iperbole ha due assi di simmetria, è anche il centro di simmetria.
Vertici (A e A’) : sono i punti di intersezione dei rami dell’iperbole con l’asse focale.
Raggi vettoriali (R) : sono i segmenti che vanno da qualsiasi punto dell’iperbole a ciascun fuoco.
Lunghezza focale : è la lunghezza del segmento composito tra i due fuochi.
Asse maggiore o asse reale: è il segmento che va dal punto A al punto A’, la sua lunghezza è equivalente a
$2a.$
Asse piccolo o asse immaginario: è il segmento che va dal punto B al punto B’, la sua lunghezza è equivalente a
$2b.$
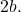
Asintoti : sono le linee tratteggiate mostrate sul grafico. Vedremo di seguito come vengono calcolati.

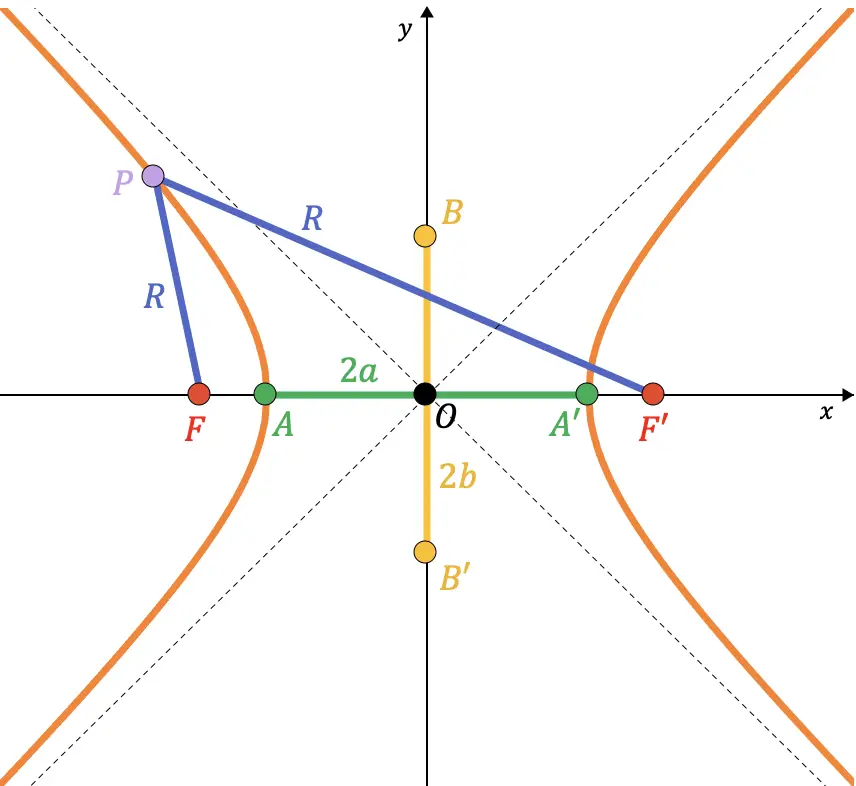
Relazione tra gli elementi di un’iperbole

Innanzitutto diciamo che semiasse significa metà di un asse. Ad esempio, il semiasse vero è il segmento che va dal punto A al centro dell’iperbole, la cui lunghezza è

$a.$

Esiste quindi una relazione molto importante tra il semiasse reale, il semiasse immaginario e la semilunghezza focale. In effetti, la formula che dedurremo di seguito è molto utilizzata per risolvere esercizi e problemi sull’iperbole.

Dovresti sapere che i punti B e B’ di un’iperbole corrispondono ai punti di intersezione dell’asse principale e del cerchio immaginario di raggio

$c$

(distanza semifocale) dal centro al punto A. Pertanto, come si può vedere nella seguente rappresentazione grafica, il segmento che congiunge il punto A ed il punto B coincide con il raggio di detto cerchio (

$c$

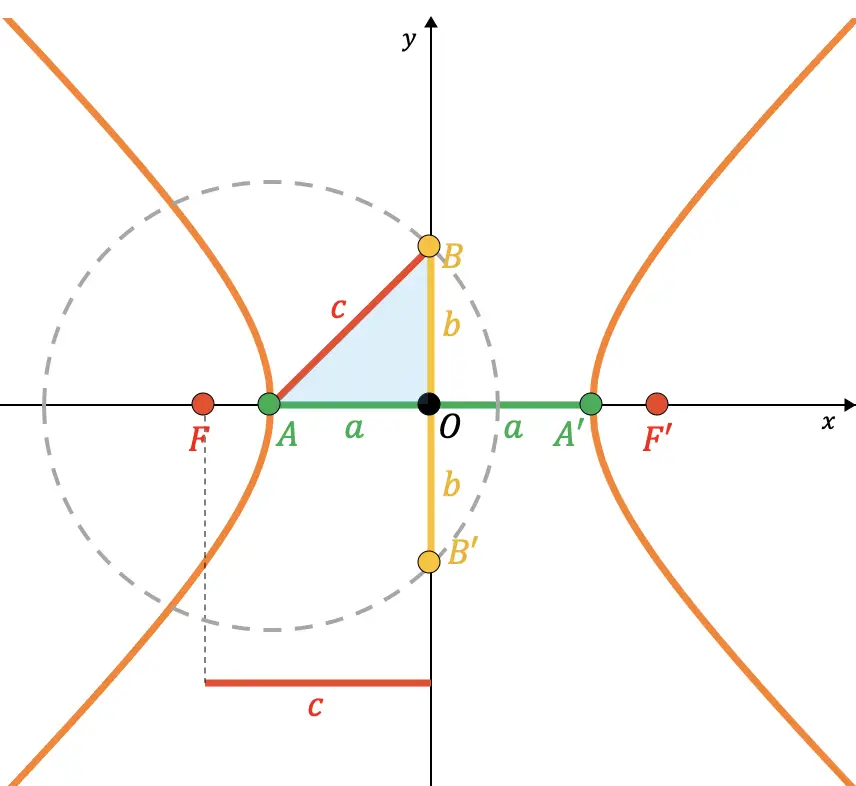
Relazione tra gli elementi di un'iperbole

Quindi si può dimostrare dal teorema di Pitagora che la relazione tra i parametri

$a, b$

$c$

è il seguente:

$c^2 = a^2+b^2$

equazione dell’iperbole

Esistono diversi tipi di equazioni dell’iperbole, poiché a seconda delle sue proprietà l’una o l’altra viene utilizzata per esprimerla matematicamente. Successivamente, analizzeremo ciascuno in dettaglio.

Innanzitutto, abbiamo l’ equazione ordinaria dell’iperbole. In secondo luogo vedremo una variante dell’equazione ordinaria, questa è l’ equazione ridotta o canonica dell’iperbole. Successivamente studieremo come è l’ equazione generale di un’iperbole. E infine, analizzeremo le equazioni di due casi speciali di iperboli: l’ iperbole equilatera e le iperboli coniugate .

Equazione ordinaria dell’iperbole

Quando vogliamo definire mediante un’equazione un’iperbole con centro esterno nell’origine delle coordinate (punto (0,0)), dobbiamo utilizzare la seguente formula:

La formula per l’ equazione ordinaria dell’iperbole in coordinate cartesiane è la seguente:

$\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1$

Oro:

$x_0$

E

$y_0$

sono le coordinate del centro dell’iperbole:

$O(x_0,y_0)$
$a$

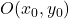
è la lunghezza del semiasse maggiore dell’iperbole.
$b$

è la lunghezza del semiasse minore dell’iperbole.

Con questa equazione puoi descrivere le iperboli il cui asse focale è orizzontale (rami aperti a sinistra e a destra), che è ciò che normalmente sono le iperboli. Ma se lavoriamo con un asse focale verticale (rami aperti dall’alto verso il basso), il segno negativo passa dalla variabile y alla variabile x :

$\cfrac{(y-y_0)^2}{a^2}-\cfrac{(x-x_0)^2}{b^2} = 1$

Oro

$x_0$

$y_0$

sono, come prima, le coordinate del centro dell’iperbole e i termini

$a$

$b$

sono ancora il semiasse maggiore e il semiasse minore dell’iperbole, anche se, a differenza di prima, questi due saranno ora orientati rispettivamente verticalmente e orizzontalmente.

Equazione canonica o ridotta dell’iperbole

Questo tipo di equazione dell’iperbole è molto simile all’equazione ordinaria, l’unica differenza è che l’equazione canonica viene utilizzata per esprimere analiticamente le iperboli il cui centro è il punto (0,0). Utilizziamo quindi l’equazione canonica o ridotta dell’iperbole quando il centro dell’iperbole è l’origine delle coordinate.

Dedurremo ora la formula per l’equazione ridotta dell’iperbole dalla sua equazione ordinaria:

$\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1$

Se il centro dell’iperbole dovesse essere l’origine delle coordinate, cioè il punto (0,0), vale sempre quanto segue:

$x_0 = 0$

$y_0 = 0$

Pertanto, la formula dell’equazione canonica o ridotta dell’iperbole sarà:

$\color{orange} \boxed{\color{black}\qquad\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1 \vphantom{\cfrac{\vphantom{\Bigl(}}{\vphantom{\Bigl(}}}\qquad }$

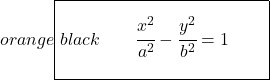
Come prima, se l’asse focale fosse verticale anziché orizzontale, la variabile negativa sarebbe x :

$\cfrac{y^2}{a^2}-\cfrac{x^2}{b^2} = 1$

Equazione generale dell’iperbole

La formula per l’equazione generale di un’iperbole è la seguente:

$Ax^2 +Bxy+Cy^2 +Dx+Ey+F =0$

Tuttavia, affinché l’equazione di cui sopra sia un’iperbole, i coefficienti

$A$

$C$

Devono essere diversi da zero e, allo stesso tempo, avere segno opposto.

Equazione dell’iperbole equilatera

Un’iperbole equilatera è un’iperbole in cui la lunghezza del semiasse reale è equivalente alla lunghezza del semiasse immaginario, ciò significa che

$a=b.$

Pertanto l’equazione dell’iperbole equilatera è:

$\cfrac{x^2}{a^2}-\cfrac{y^2}{a^2} = 1$

Inoltre, gli asintoti delle iperboli equilatere sono perpendicolari tra loro. E le equazioni di queste linee sono le seguenti:

$y=x$

$y=-x$

Se guardiamo attentamente, queste due equazioni sono le bisettrici rispettivamente del primo (e terzo) quadrante e del secondo (e quarto) quadrante. Quindi se ruotiamo un’iperbole equilatera di 45° verso sinistra, i suoi asintoti occupano il posto degli assi coordinati:

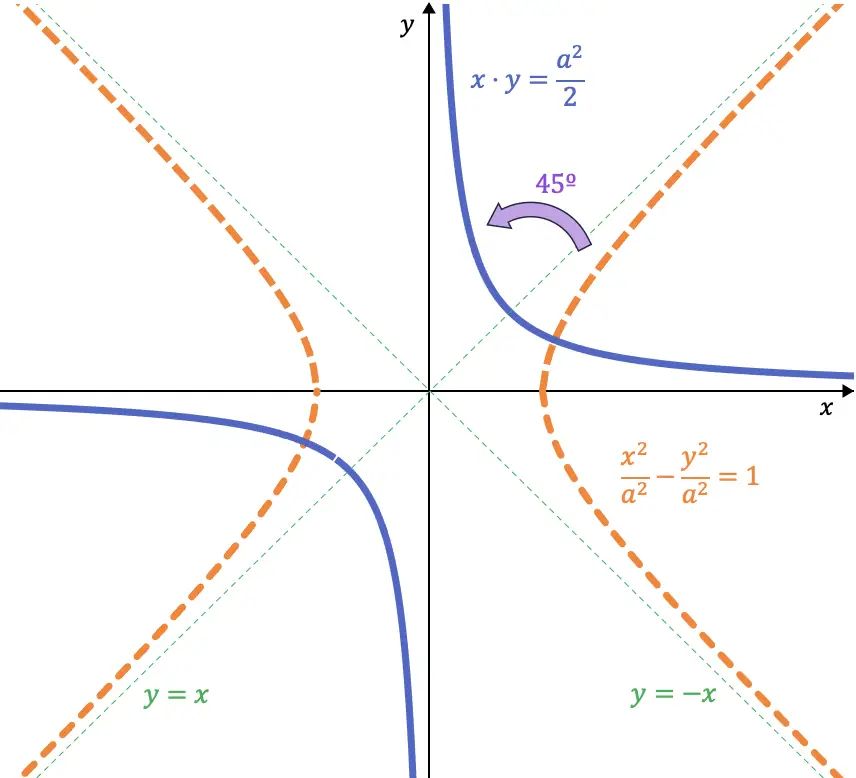
Quindi, quando compiamo la svolta di 45º, l’equazione per l’iperbole è:

$x\cdot y = \cfrac{a^2}{k}$

iperboli coniugate

Due iperboli sono coniugate se l’asse reale dell’una è equivalente all’asse immaginario dell’altra . Pertanto, l’unica differenza tra le equazioni di due iperboli coniugate è quale variabile è negata, perché i coefficienti dei denominatori devono rimanere gli stessi.

Ecco un esempio delle equazioni di due iperboli coniugate tra loro:

$\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2}=1 \qquad \qquad \cfrac{y^2}{b^2}-\cfrac{x^2}{a^2} =1$

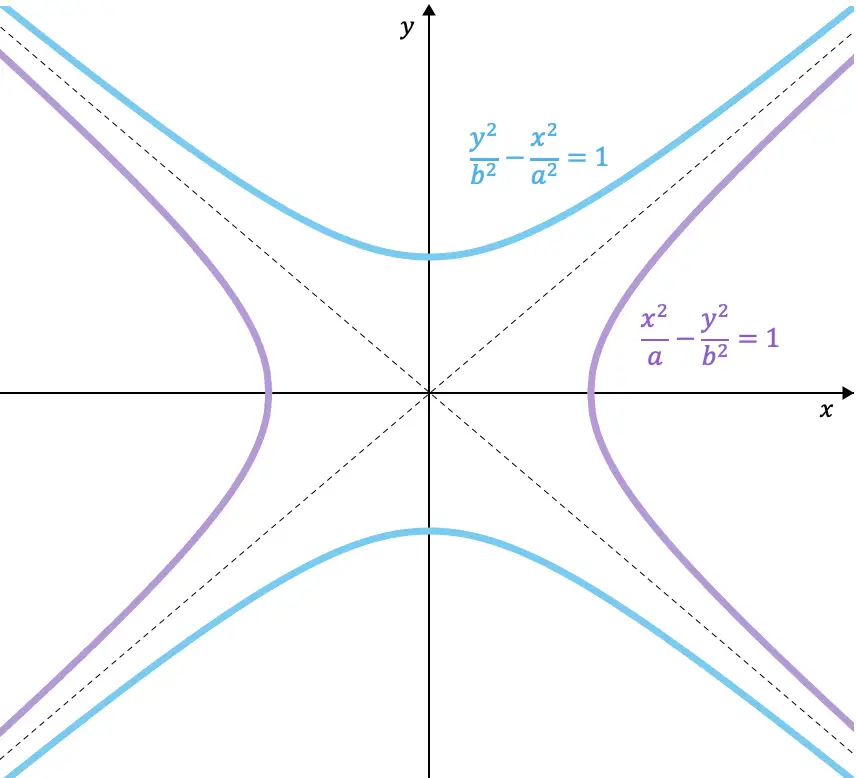
Inoltre, come puoi vedere dalle iperboli rappresentate graficamente, le iperboli coniugate condividono gli stessi asintoti.

Asintoti dell’iperbole

Come hai visto nei grafici precedenti, ogni iperbole ha due asintoti. Ricorda che un asintoto è una linea retta che si avvicina molto a una funzione ma non la interseca né la tocca mai del tutto.

Quindi le formule che corrispondono agli asintoti delle iperboli sono:

$y= \cfrac{b}{a} x$

$y= -\cfrac{b}{a}x$

In modo che gli asintoti di qualsiasi iperbole possano essere facilmente determinati utilizzando i loro coefficienti

$a$

$b,$

che sono rispettivamente le lunghezze del semiasse reale e del semiasse immaginario dell’iperbole.

Eccentricità dell’iperbole

L’ eccentricità di un’iperbole è un parametro caratteristico che determina quanto è aperta o chiusa. Numericamente, l’eccentricità di un’iperbole si calcola dividendo la sua semilunghezza focale per il suo semiasse reale:

$e=\cfrac{c}{a}$

L’eccentricità di qualsiasi iperbole è sempre maggiore di 1:

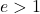
$e>1″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”40″ style=”vertical-align: -2px;”></p> </p> <p> Il valore di questo parametro è abbastanza rilevante, poiché indica la forma di una data iperbole. Quanto più l’eccentricità di un’iperbole è vicina a 1, tanto più chiusi saranno i suoi rami; invece quanto maggiore sarà il valore dell’eccentricità tanto più i suoi rami saranno aperti. </p> <figure class=$

Va infine notato che l’eccentricità di un’iperbole equilatera è sempre uguale a

$\sqrt{2}.$

Problemi di iperbole risolti

Di seguito puoi mettere in pratica i concetti che abbiamo visto con problemi ed esercizi risolti sulle iperboli e sull’equazione dell’iperbole.

Esercizio 1

Qual è l’equazione dell’iperbole con centro nel punto (-1,3), lunghezza del semiasse reale di 3 unità e lunghezza del semiasse immaginario (parallelo all’asse Y) di 7 unità?

vedi soluzione

Per trovare l’equazione dell’iperbole, basta applicare la formula dell’equazione ordinaria dell’iperbole:

$\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1$

Sostituiamo le coordinate del centro dell’iperbole nell’equazione:

$\cfrac{(x-(-1))^2}{a^2}-\cfrac{(y-3)^2}{b^2} = 1$

$\cfrac{(x+1)^2}{a^2}-\cfrac{(y-3)^2}{b^2} = 1$

E infine, sostituiamo i valori delle incognite

$a$

$b:$

$\cfrac{(x+1)^2}{3^2}-\cfrac{(y-3)^2}{7^2} = 1$

$\cfrac{\bm{(x+1)^2}}{\bm{9}}\bm{-}\cfrac{\bm{(y-3)^2}}{\bm{49}} \bm{= 1}$

Esercizio 2

Trova le coordinate del centro, dei vertici, dei fuochi, il valore dell’eccentricità e gli asintoti dell’iperbole la cui equazione è definita da:

$\cfrac{x^2}{25}-\cfrac{y^2}{144} = 1$

vedi soluzione

Innanzitutto occorre notare che la variabile negativa nell’equazione è la variabile y , quindi i rami dell’iperbole si apriranno a destra e a sinistra (asse focale parallelo all’asse X).

In secondo luogo, l’equazione corrisponde all’equazione canonica (o ridotta) dell’iperbole, quindi il suo centro è l’origine delle coordinate.

$\bm{O(0,0)}$

Una volta conosciuto il centro dell’iperbole, per calcolare tutto il resto occorre trovare il valore del semiasse reale (parametro

$a$

) e il semiasse immaginario (parametro

$b$

). Possiamo dedurli entrambi dalla formula dell’equazione canonica (o ridotta) dell’iperbole:

$\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1$

$\cfrac{x^2}{25}-\cfrac{y^2}{144} = 1$

$a^2 = 25$

$a = \sqrt{25}$

$a = 5$

$b^2 = 144$

$b= \sqrt{144}$

$b = 12$

Quindi se tra il centro ed i vertici c’è una distanza di 5 unità, ciò implica che i vertici delle iperboli sono:

$\bm{A(-5,0) \qquad A'(5,0)}$

Per determinare le coordinate di ciascun punto focale è necessario conoscere il valore della mezza focale (parametro

$c$

). E per questo possiamo usare la formula che collega gli elementi di un’iperbole:

$c^2 = a^2+b^2$

$c = \sqrt{a^2+b^2}$

$c = \sqrt{5^2+12^2} = \sqrt{169} =13$

Tra il centro e le abitazioni c’è quindi uno spazio di 13 unità. Pertanto, le coordinate di ciascuna famiglia sono:

$\bm{F(-13,0) \qquad F'(13,0)}$

Quindi, per calcolare l’eccentricità dell’iperbole, dobbiamo utilizzare la formula corrispondente:

$e= \cfrac{c}{a} = \cfrac{13}{5} = \bm{2,6}$

E, infine, troviamo gli asintoti dell’iperbole con le loro formule:

$y= \cfrac{b}{a} x \ \longrightarrow \ \bm{y=}\mathbf{\cfrac{12}{5}}\bm{ x}$

$y= -\cfrac{b}{a}x \ \longrightarrow \ \bm{y=-}\mathbf{\cfrac{12}{5}}\bm{ x}$

Esercizio 3

Calcola l’equazione dell’iperbole con centro nell’origine delle coordinate sapendo che la differenza nelle distanze da un punto dell’iperbole ai fuochi F(-4.0) e F(4.0) è 6 unità.

vedi soluzione

Innanzitutto, poiché l’iperbole ha il centro nell’origine delle coordinate, utilizzeremo l’equazione canonica o ridotta:

$\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1$

Allora, secondo la definizione di iperbole, il valore assoluto della differenza delle distanze da uno dei suoi punti ai fuochi (che in questo caso è 6) deve essere uguale alla lunghezza dell’asse reale (

$2a$