In questa pagina troverai la spiegazione di quali sono le componenti (o coordinate) di un vettore. Inoltre, potrai vedere come vengono calcolati a partire da due punti e anche come vengono scomposti attraverso il loro modulo e il loro angolo. Inoltre troverai esempi ed esercizi risolti passo dopo passo.
Quali sono le componenti di un vettore?
Le componenti di un vettore sono le proiezioni di un vettore sugli assi cartesiani. Pertanto, la proiezione del vettore sull’asse x è la componente X del vettore e, analogamente, la proiezione del vettore sull’asse y è la componente Y del vettore.
Le componenti di un vettore possono anche essere chiamate coordinate di un vettore.
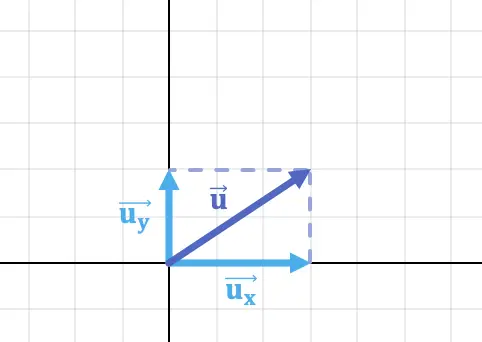
Ad esempio, la componente orizzontale e la componente verticale del vettore nell’immagine sopra sono:
![]()
![]()
Quindi il vettore è:
![]()
Pertanto, le componenti di un vettore possono anche essere definite come la rappresentazione di un vettore in un sistema di coordinate. Ovviamente se è un sistema bidimensionale (in r2) il vettore avrà due componenti, invece se è una base tridimensionale (in r3) il vettore sarà composto da tre componenti.
Le componenti cartesiane di un vettore sono così importanti perché con esse possiamo conoscere le caratteristiche del vettore, che sono principalmente la direzione, il senso e il modulo (o grandezza) del vettore. Inoltre, vengono utilizzati per eseguire operazioni sui vettori.
Come calcolare le componenti di un vettore da due punti
Abbiamo appena visto come trovare graficamente le coordinate di un vettore, possiamo però determinarne anche numericamente le sue componenti.
Per calcolare numericamente le componenti di un vettore dobbiamo conoscere due punti: la sua origine e la sua fine, ovvero dove inizia e dove finisce. Poiché le componenti di un vettore sono le coordinate che otteniamo sottraendo la sua estremità meno l’origine.
![]()
Ad esempio, calcoleremo il vettore la cui origine è il punto A(3,1) e la sua estremità è il punto B(5,4):
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{AB} & = (5,4)-(3,1) \\[1.5ex] &= (5-3,4-1) \\[1.5ex] & = \bm{(2,3)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c740536015a29149532a4a1eb46f4f7_l3.png)
Come puoi vedere, determinare le componenti di un vettore non è molto difficile, tuttavia è piuttosto importante. Ad esempio, uno dei tipi di vettori più comunemente utilizzati sono i vettori perpendicolari (o ortogonali); Bene, se capisci quali sono le coordinate di un vettore, è molto facile calcolare i vettori perpendicolari. Puoi vedere come si fa nella spiegazione dei vettori ortogonali .
Come calcolare le componenti di un vettore dal suo modulo e dal suo angolo
Puoi anche trovare le componenti di un vettore dalla sua grandezza e dall’angolo che forma con l’asse X. Questo processo è chiamato decomposizione vettoriale .
Pertanto, le componenti X e Y del vettore possono essere calcolate con i rapporti trigonometrici del coseno e del seno:

Come puoi vedere nell’immagine, il modulo di un vettore e le sue componenti completano un triangolo rettangolo, quindi è possibile applicare le formule elementari della trigonometria.
Se non ricordi come viene calcolato il modulo di un vettore, puoi cercare qual è il modulo di un vettore . Qui troverai la formula per la grandezza di un vettore, oltre ad esempi, esercizi risolti passo passo e tutte le proprietà della grandezza di un vettore. Questa è una spiegazione molto completa quindi la capirai perfettamente. ✅
A differenza della grandezza di un vettore che è sempre positiva, le sue componenti possono essere negative perché seno e coseno possono assumere valori negativi.
Ad esempio, faremo la scomposizione vettoriale del vettore il cui modulo e angolo con l’asse OX sono:
![]()
La componente X del vettore è uguale al modulo moltiplicato per il coseno dell’angolo:
![]()
E la componente Y del vettore è uguale al prodotto del modulo e del seno dell’angolo:
![]()
Quindi le coordinate del vettore sono:
![]()