In questa pagina vedrai cosa sono le matrici complesse, le matrici coniugate e le matrici trasposte coniugate. Ora ti somigliano molto, ma vedrai che alla fine della pagina capirai appieno la differenza tra ciascuno di essi. Inoltre, vedremo esempi di ciascun tipo e le sue proprietà.
matrice complessa
Prima di vedere la spiegazione della matrice coniugata e della matrice coniugata trasposta, rivediamo il concetto di matrice complessa:
Cos’è una matrice complessa?
Una matrice complessa è una matrice che ha tra i suoi elementi un certo numero complesso.
Ricordiamo che un numero complesso o immaginario è un numero composto da una parte reale e da una parte immaginaria, che viene indicata con la lettera i. Per esempio:
![]()
.
Esempi di matrici complesse
Diamo un’occhiata ad alcuni esempi di array multidimensionali complessi:
Esempio di matrice complessa di ordine 2 × 2
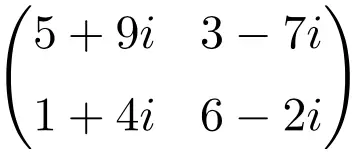
Esempio di matrice complessa di dimensione 3×3
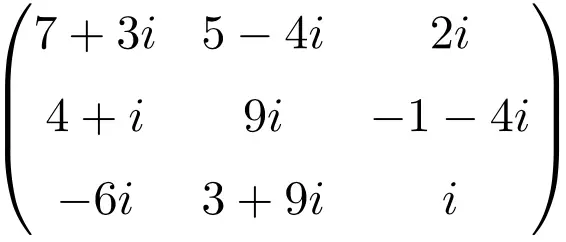
Esempio di matrice complessa di dimensione 4×4
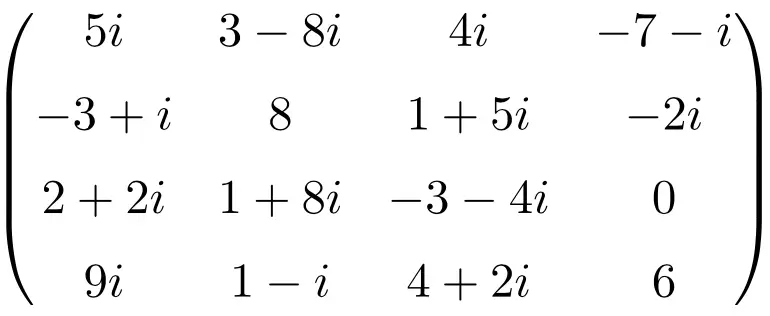
matrice coniugata
Una volta vista qual è la definizione di matrice complessa, vediamo cosa sono una matrice coniugata e una matrice coniugata trasposta:
Cos’è una matrice coniugata?
Una matrice coniugata è una matrice complessa in cui tutti i suoi elementi sono stati sostituiti dai loro coniugati, cioè il segno della parte immaginaria di tutti i suoi numeri complessi è stato cambiato.
La matrice coniugata di
![]()
è espresso da una barra orizzontale sopra:
![]()
.
Esempio di matrice coniugata
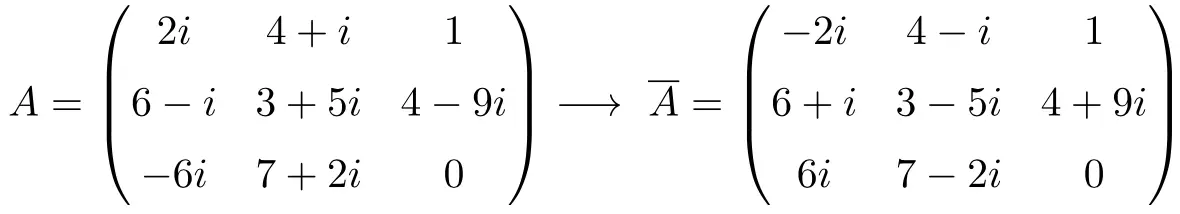
Proprietà della matrice coniugata
Le caratteristiche di questo tipo di matrice sono le seguenti:
- Il coniugato di una matrice coniugata è la matrice originale.
![]()
- Aggiungere (o sottrarre) due matrici e coniugare il risultato equivale a coniugare prima le due matrici separatamente e poi addizionarle (o sottrarle).
![]()
- Il prodotto coniugato di due matrici equivale a coniugare le due matrici separatamente e quindi calcolare la moltiplicazione della matrice.
![]()
- Moltiplicare una matrice per uno scalare e coniugare il risultato equivale a fare prima i coniugati dello scalare e della matrice, quindi risolvere il prodotto.
![]()
- Trasporre una matrice e poi coniugarla significa prima coniugare la matrice e poi trasporla.
![]()
- Fare l’ inverso di una matrice e poi coniugarla equivale a coniugare la matrice e poi invertirla.
![]()
- Il rango di una matrice coniugata è uguale al rango della stessa matrice non coniugata.
![]()
- È indifferente calcolare la traccia di una matrice coniugata oppure calcolare la traccia della stessa matrice senza coniugazione e poi coniugare il risultato.
![]()
- Infine, prendere il determinante di una matrice coniugata equivale a calcolare il coniugato del risultato del determinante della stessa matrice senza coniugazione.
![]()
Matrice di trasposizione coniugata
Infine, dopo aver visto come coniugare una matrice, passiamo al concetto di matrice trasposta coniugata:
Cos’è una matrice di trasposizione coniugata (o trasposizione)?
La matrice coniugata trasposta (o trasposta) è quella ottenuta dopo aver trasposto una matrice e poi realizzato il suo coniugato.
Questo tipo di matrice è chiamata anche matrice aggiunta o semplicemente matrice aggiunta. Inoltre, di solito è rappresentato da un asterisco
![]()
, anche se ci sono matematici che lo disegnano come
![]()
O
![]()
.
Esempio di matrice di trasposizione coniugata
Ecco un esempio di calcolo della trasposizione (o trasposizione coniugata) di una matrice:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4fc37df446a4600709c54e8b1b78072_l3.png)
Per prima cosa trasponiamo la matrice A:
![Rendered by QuickLaTeX.com \displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdc97bb655f8e2f18abbc2e6d480c02b_l3.png)
E poi calcoliamo la matrice coniugata della trasposta, o in altre parole, cambiamo il segno della parte immaginaria di tutti i numeri complessi:
![Rendered by QuickLaTeX.com \displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-209bcf07d842e6157663ddc03909d544_l3.png)
Pertanto, la sintesi del calcolo della matrice di trasposizione coniugata è:
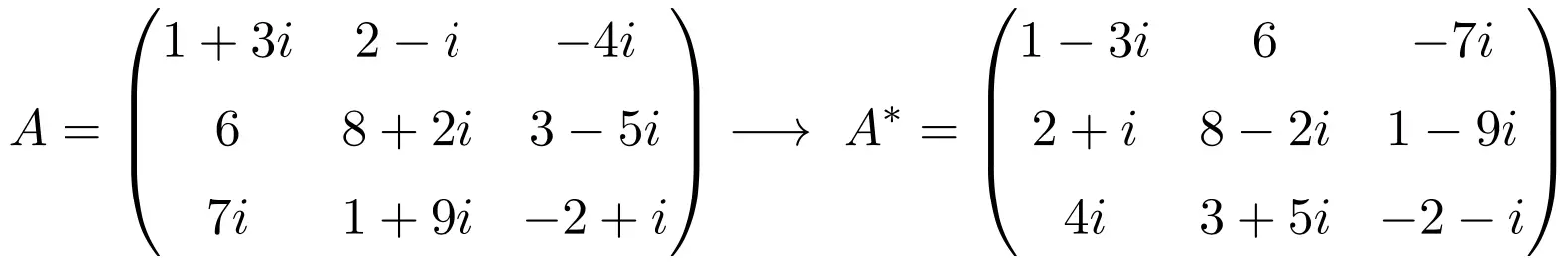
Proprietà della matrice di trasposizione coniugata
Le proprietà di questo tipo di matrice quadrata sono le seguenti:
- La matrice trasposta coniugata di una matrice precedentemente trasposta e coniugata è la matrice originale.
![]()
- La proprietà di addizione delle matrici di trasposizione coniugata afferma che aggiungere (o sottrarre) due matrici e quindi applicare questa operazione al risultato equivale a eseguire prima la trasposizione coniugata di ciascuna matrice e quindi ad aggiungere (o sottrarre) i risultati.
![]()
- Moltiplicando due matrici e poi eseguendo la trasposizione coniugata si ottiene lo stesso risultato del prodotto inverso delle matrici trasposte coniugate.
![]()
- Calcolare la trasposizione coniugata del prodotto di uno scalare e una matrice equivale a coniugare il numero complesso e trovare la trasposizione coniugata della matrice separatamente e quindi moltiplicare.
![]()
- Se la matrice è invertibile, l’ordine in cui vengono eseguite le operazioni di inversione della matrice e di trasposizione coniugata è irrilevante.
![]()