È molto comune rappresentare funzioni per poter analizzare graficamente la relazione tra le diverse variabili che compongono questa funzione. Oppure a volte questi tipi di rappresentazioni vengono addirittura utilizzati per acquistare più funzionalità. Questo è particolarmente utilizzato quando si eseguono studi statistici. Detto questo, oggi ti spiegheremo un metodo molto semplice che consiste di soli 3 passaggi per poter rappresentare graficamente qualsiasi funzione. Inoltre, discuteremo anche come analizzare il risultato grafico per trarre conclusioni.
Tipi di funzioni
Innanzitutto, dobbiamo comprendere le caratteristiche dei diversi tipi di funzioni e quali differenze dovrebbero essere considerate nel rappresentarle. In questo modo ci sarà più semplice realizzare la rappresentazione grafica, motivo per cui ora commenteremo brevemente ciascuna tipologia. Vale la pena notare che esistono molti tipi di funzioni, quindi ci concentreremo sui due tipi più importanti di funzioni polinomiali e funzioni a tratti.
funzioni lineari
La funzione lineare o funzione polinomiale di primo grado è la funzione la cui espressione è un polinomio di grado 1. Quindi, la sua espressione segue il modello f(x) = mx + n , dove m è la pendenza e n è l’ordinata. Fondamentalmente queste funzioni hanno una forma grafica equivalente ad una linea. Di seguito puoi vedere un esempio:
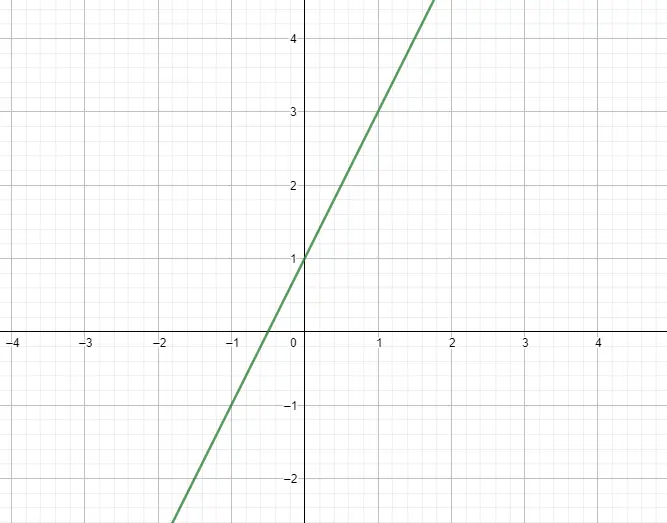
funzioni quadratiche
La funzione quadratica o funzione parabolica si esprime mediante un polinomio di secondo grado e per questo ha forma parabolica. Come modello da seguire prenderemo in considerazione la seguente espressione: f(x) = ax² + bx + c, dove a ≠ 0. Inoltre, ci sono altre due caratteristiche notevoli di queste funzioni, l’ampiezza e la crescita. Di seguito puoi vedere un esempio:
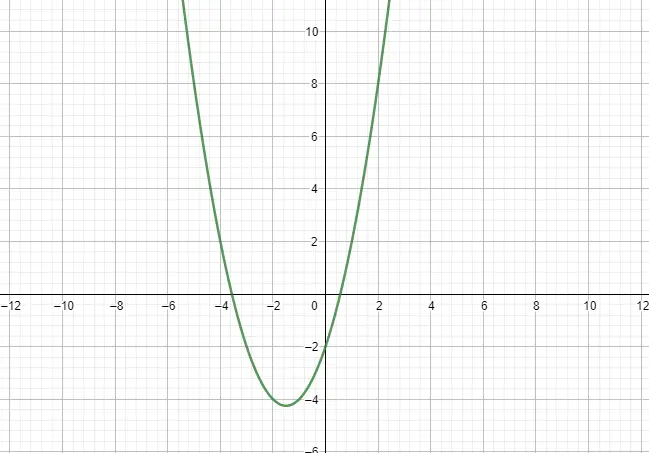
Funzioni a tratti
Una funzione definita a tratti è una funzione che ha definizioni diverse a seconda del valore di x. Quindi, quando x occupa un certo intervallo di valori, dobbiamo provare un’espressione. Quando invece la x occupa altri valori è necessario elaborare un’espressione diversa. È qui che troviamo le discontinuità e quindi i limiti. Poiché dove finisce una funzione può iniziarne un’altra, ma senza collegarsi direttamente. Di seguito puoi vedere un esempio:
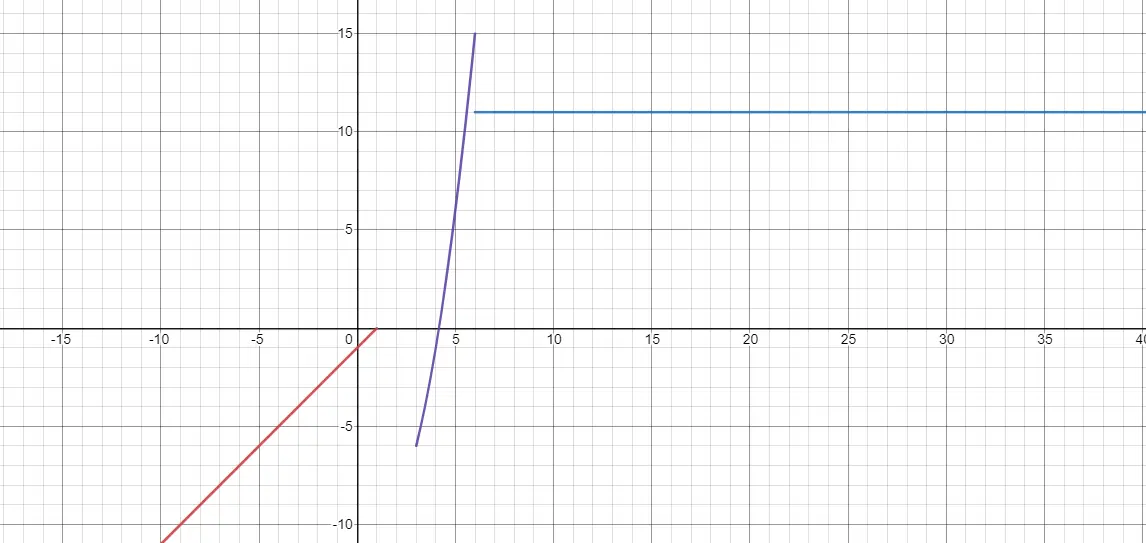
Come rappresentare le funzioni lineari?
Per rappresentare graficamente una funzione lineare, dobbiamo seguire tre passaggi molto semplici. Successivamente spiegheremo la procedura, anche se se vuoi imparare a rappresentare graficamente le funzioni paraboliche ti consigliamo di consultare la sezione successiva.
Creare una tabella di valori
Per poter rappresentare graficamente una funzione, dobbiamo creare una tabella di valori in cui scriveremo tutti i valori delle variabili. In sostanza questo ci permetterà di stabilire una relazione tra le due variabili e in questo modo potremo tracciare il percorso della funzione. Se non sai come creare una tabella di valori, puoi guardare quest’ultimo collegamento. Anche se in sintesi, consiste nel dare un valore alla variabile indipendente e nel sostituire l’incognita nella funzione che la riguarda. Avremo quindi i due numeri associati, la tabella seguente ne mostra un esempio:
Dalla funzione f(x) = 2x+1:
| X | f(x) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
Disegna punti sul grafico e uniscili disegnando la funzione
Una volta realizzata la tabella possiamo iniziare a disegnare i punti su un grafico. Lo facciamo associando la variabile indipendente all’asse x e l’altra all’asse y, e in questo modo otterremo i punti. Puoi disegnare quanti punti vuoi, anche se per rappresentare funzioni di questo stile di solito è sufficiente calcolare cinque punti. Da allora, hanno seguito un percorso rettilineo e, pertanto, continua ad essere lo stesso, non importa quanto lontano si avanzi.
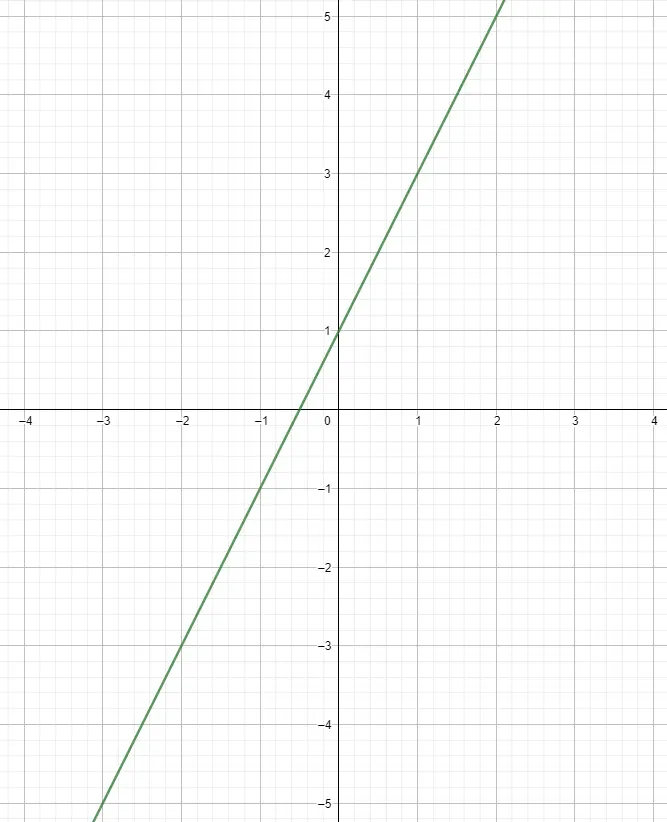
Utilizzo della pendenza per rappresentare graficamente una funzione lineare
Esiste un secondo metodo per poter rappresentare graficamente funzioni lineari senza tabelle di valori, che consiste nel calcolare la pendenza della funzione: m = (variazione verticale / variazione orizzontale). Quindi una volta calcolata la pendenza bisogna guardare il punto di partenza. Ritornando all’esempio precedente f(x) = 2x+1, sappiamo che il punto di partenza sarà (0, 1), perché a x = 0 il computer = 1 (lo deduciamo dal +1 nell’espressione) . E poi basta aggiungere la pendenza, che in questo caso è pari a +2 verticale per 1 orizzontale. Allora sapremo che il punto successivo sarà (1,3).
Come rappresentare le funzioni quadratiche?
Per rappresentare una funzione quadratica possiamo seguire due metodi, il primo prevede tabelle di valori. E la seconda consiste nel calcolare una serie di punti chiave: il vertice, i punti di intersezione con l’asse X e il punto di intersezione con l’asse Y. Quest’ultimo è quello che spiegheremo di seguito:
Calcola il vertice di una parabola
Esistono due formule che ci permettono di calcolare il vertice di una funzione parabolica, sostanzialmente una ci dà il punto di vertice dell’asse X e l’altra ci dà il punto di vertice dell’asse Y. Puoi trovare entrambe le formule di seguito, ma entrambe hanno una struttura simile.
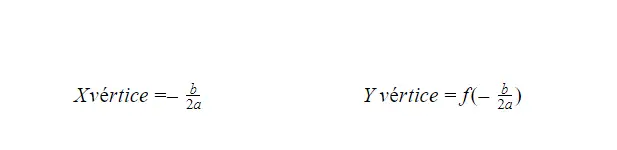
Calcolare i punti di intersezione con l’asse X di una funzione quadratica
Per ottenere i punti di intersezione delle non dovremo fare altro che risolvere l’equazione e avremo già i valori di X che stiamo cercando. Vale la pena notare che essendo una funzione quadratica otterremo due risultati, non solo uno.
Calcolare il punto di intersezione con l’asse Y di una funzione quadratica
Infine, per ottenere il punto di intersezione con l’asse Y basta calcolare c = f(0). E poiché una parabola interseca sempre l’asse verticale (ordinate) quando x = 0, allora diremo che il punto di taglio dell’asse Y sarà (0,c). Una volta che abbiamo tutti questi punti possiamo disegnarli sul grafico e non ci resta che unirli disegnando la parabola in questo modo.
Come rappresentare le funzioni a tratti?
Per poter rappresentare le funzioni in pezzi, puoi mescolare tutti i metodi che abbiamo spiegato in precedenza. Poiché le funzioni di questo stile sono composte da tutti i tipi di funzioni di cui abbiamo parlato. Pertanto ce ne saranno alcuni che dovrai calcolare tramite una tabella di valori ed altri che dovrai calcolare con altri metodi. Tuttavia, una volta che avrai padroneggiato quelli che ti abbiamo spiegato in questo articolo, non avrai più problemi a rappresentare le funzioni in pezzi.
D’altra parte, poiché quando li rappresenti devi fare uno studio di continuità, ti consigliamo di imparare come risolvere i limiti , se non sai già come. Questo ti aiuterà a rappresentare correttamente gli endpoint di ciascuna funzione. Detto questo, ora sarai pronto per rappresentare graficamente le funzioni a tratti e anche qualsiasi altro tipo di funzione. Vi lasciamo ora con una serie di consigli grafici e con una spiegazione molto utile sulla capacità della calcolatrice di creare grafici.
Come realizzare grafici con la calcolatrice?
Se hai una calcolatrice grafica , avrà la capacità di tracciare grafici. Il che può essere molto semplice da fare una volta che conosci la procedura, ma se ancora non sai come farlo, ora te lo spiegheremo.
- Accedi alla modalità grafica: il primo passo è accedere all’opzione grafica o rappresentazioni grafiche dal menu. Questa opzione potrebbe essere etichettata con un nome diverso per la tua calcolatrice, ma conterrà parole simili a grafica o a quelle di cui abbiamo già parlato.
- Personalizzare le opzioni del grafico: una volta entrati nell’editor del grafico, dobbiamo dare un nome al file, etichettare gli assi, selezionare il numero di elementi che verranno rappresentati graficamente e configurare le opzioni estetiche della rappresentazione. Questo è un passo molto veloce da fare.
- Somma i punti della funzione: puoi poi iniziare ad sommare i punti che formeranno la figura. Puoi farlo scrivendo i punti con la seguente notazione: (0,1), (3,2)… E continuerai ad aggiungere i punti finché non avrai finito il grafico.
- Utilizza la funzione “Anteprima”: una volta terminato il progetto, puoi visualizzare in anteprima il risultato e vedere se risulta come previsto. Inoltre, molti modelli dispongono di opzioni di modifica con questa anteprima, quindi puoi modificare il risultato fino a renderlo perfetto.
- Salva il progetto: una volta completata l’intera procedura di modifica, ricordati di salvarlo in una posizione facile da ricordare. In questo modo, ogni volta che ne avrai bisogno, potrai accedere nuovamente al progetto per visionarlo o apportare le migliorie che desideri.
I migliori calcolatori per rappresentare le funzioni
Se sei interessato all’acquisto di un modello grafico per poter rappresentare le funzioni sulla stessa calcolatrice, ti consigliamo due modelli: l’ HP 50G e l’ HP Prime . Si tratta di due modelli di altissima qualità, anche se sono costosi, quindi devi chiederti se vale la pena investire per te. Ad esempio, se hai intenzione di intraprendere una carriera molto complessa dal punto di vista matematico, come l’ingegneria, allora ti consigliamo vivamente di acquistare uno di questi due modelli. Ma se non hai bisogno di tanta potenza di calcolo o grafica, forse Casio FX-9750GII sarà sufficiente per te.
Come rappresentare graficamente le funzioni online?
Puoi sempre scegliere la possibilità di utilizzare programmi di grafica online, come: Desmos , Geogebra e molti altri. In questo modo otterrai grafici molto accurati in modo rapido. Possiamo dire che la forma numerica viene utilizzata quando si vogliono rappresentare graficamente funzioni in modo semplice e veloce. D’altra parte, se desideri rappresentare graficamente le funzioni in modo da poterle modificare (cambiare tutti i loro attributi) e avere risorse di analisi delle funzioni di alta qualità a portata di mano, allora ti consigliamo di acquistare una calcolatrice scientifica.