Come diagonalizzare una matrice -

In questa pagina troverai tutto sulle matrici diagonalizzabili: cosa sono, quando possono essere diagonalizzate e quando no, il metodo per diagonalizzare le matrici, le applicazioni e le proprietà di queste particolari matrici, ecc. E hai anche diversi esercizi risolti passo dopo passo così puoi esercitarti e capire perfettamente come vengono diagonalizzati. Infine, impareremo anche come eseguire diagonalizzazioni di matrici con il programma per computer MATLAB, poiché è utilizzato molto frequentemente.

Cos’è una matrice diagonalizzabile?

Come vedremo in seguito, diagonalizzare una matrice è molto utile nel campo dell’algebra lineare. Questo è il motivo per cui molti si chiedono… cos’è la diagonalizzazione della matrice? Ebbene, la definizione di matrice diagonalizzabile è:

Una matrice diagonalizzabile è una matrice quadrata che può essere trasformata in una matrice diagonale, cioè una matrice piena di zeri tranne che sulla diagonale principale. La diagonalizzazione delle matrici è scomposta come segue:

$A = PDP^{-1}$

O equivalente,

$D = P^{-1}AP$

Oro

$A$

è la matrice da diagonalizzare,

$P$

è la matrice le cui colonne sono gli autovettori (o autovettori) di

$A$

$P^{-1}$

la sua matrice inversa e

$D$

è la matrice diagonale formata dagli autovalori (o autovalori) di

$A$

La matrice

$P$

agisce come una base che cambia matrice, quindi in realtà con questa formula cambiamo la base in matrice

$A$

, in modo che la matrice diventi una matrice diagonale (

$D$

) nella nuova sede.

Pertanto, la matrice

$A$

e la matrice

$D$

Sono matrici simili. E ovviamente,

$P$

È una matrice regolare o non degenere.

Quando puoi diagonalizzare una matrice?

Non tutte le matrici possono essere diagonalizzate; solo le matrici che soddisfano determinate caratteristiche possono essere diagonalizzate. Si può capire se una matrice è diagonalizzabile in diversi modi:

Una matrice quadrata di ordine n è diagonalizzabile se ha n autovettori (o autovettori) linearmente indipendenti , o in altre parole, se questi vettori formano una base. Questo perché la matrice
$P$

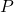
, che serve per diagonalizzare una matrice, è formato dagli autovettori di detta matrice. Per sapere se gli autovettori sono LI è sufficiente il determinante della matrice

$P$

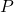
è diverso da 0, il che significa che la matrice ha il rango massimo.

$\text{si} \quad \text{det}(P)\neq 0 \ \longrightarrow \ \text{matriz diagonalizable}$

Una proprietà degli autovalori e degli autovettori è che gli autovettori di autovalori diversi sono linearmente indipendenti. Pertanto, se tutti gli autovalori della matrice sono unici, la matrice è diagonalizzabile.

Un altro modo per determinare se una matrice può essere sistemata in una matrice diagonale è utilizzare le molteplicità algebriche e geometriche. La molteplicità algebrica è il numero di volte in cui un autovalore (o autovalore) viene ripetuto e la molteplicità geometrica è la dimensione del nucleo (o nucleo) della matrice sottraendo l’autovalore sulla sua diagonale principale. Quindi, se per ogni autovalore la molteplicità algebrica è uguale alla molteplicità geometrica , la matrice è diagonalizzabile.

$\alpha_\lambda = \text{multiplicidad algebraica} = \text{multiplicidad del valor propio}$

$m_\lambda = \text{multiplicidad geom\'etrica} = \text{dim } Ker(A-\lambda I) = n -rg(A-\lambda I)$

$\alpha_\lambda \geq m_\lambda \geq 1$

$\text{si} \quad \alpha_\lambda = m_\lambda \quad \forall \lambda \ \longrightarrow \ \text{matriz diagonalizable}$

Esiste infine un teorema, il teorema spettrale, che garantisce la diagonalizzazione delle matrici simmetriche con numeri reali. In altre parole, qualsiasi matrice reale e simmetrica è diagonalizzabile .

Come diagonalizzare una matrice

La procedura per diagonalizzare una matrice si basa sulla ricerca degli autovalori (o autovalori) e degli autovettori (o autovettori) di una matrice. Questo è il motivo per cui è importante padroneggiare come calcolare gli autovalori (o autovalori) e gli autovettori (o autovettori) di qualsiasi matrice . Puoi ricordare come è stato fatto cliccando sul link, dove spieghiamo passo dopo passo come trovarli e alcuni trucchi che rendono i calcoli molto più semplici. Inoltre, troverai anche esercizi risolti per esercitarti.

Con il seguente metodo puoi diagonalizzare una matrice di qualsiasi dimensione: 2×2, 3×3, 4×4, ecc. I passi da seguire per diagonalizzare una matrice sono:

Ottenere gli autovalori (o autovalori) della matrice.
Calcolare l’autovettore associato a ciascun autovalore.
Costruisci la matrice
$P$

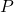
, le cui colonne sono gli autovettori della matrice da diagonalizzare.
Verifica che la matrice sia diagonalizzabile (deve soddisfare una delle condizioni spiegate nella sezione precedente).
Costruisci la matrice diagonale
$D$

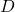
, i cui elementi sono tutti 0 tranne quelli sulla diagonale principale, che sono gli autovalori trovati nel passaggio 1.

Avvertenza: Gli autovettori della matrice

$P$

possono essere posizionati in qualsiasi ordine, tranne gli autovalori della matrice diagonale

$D$

Devono essere posizionati nello stesso ordine. Ad esempio, il primo autovalore della matrice diagonale

$D$

deve essere quello che corrisponde all’autovettore della prima colonna della matrice

$P$

Di seguito sono riportati diversi esercizi passo passo di diagonalizzazione della matrice con cui puoi esercitarti.

Risolti gli esercizi di diagonalizzazione della matrice

Esercizio 1

Diagonalizza la seguente matrice quadrata di dimensione 2×2:

$\displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}$

Vedi la soluzione

Dobbiamo innanzitutto determinare gli autovalori della matrice A. Calcoliamo quindi l’equazione caratteristica risolvendo il seguente determinante:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4$

Calcoliamo ora le radici del polinomio caratteristico:

$\displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}$

Una volta ottenuti gli autovalori si calcola l’autovettore associato a ciascuno. Innanzitutto, l’autovettore corrispondente all’autovalore 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}$

E poi calcoliamo l’autovettore associato all’autovalore 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}$

Costruiamo la matrice

$P$

, formato dagli autovettori della matrice:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}$

Poiché tutti gli autovalori sono diversi, la matrice A è diagonalizzabile. Quindi la matrice diagonale corrispondente è quella che ha gli autovalori sulla diagonale principale:

$\displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Ricordare che gli autovalori devono essere posizionati nello stesso ordine in cui gli autovettori sono posizionati nella matrice

$P$

In conclusione, la matrice del cambiamento di base e la matrice diagonalizzata sono:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Esercizio 2

Diagonalizza la seguente matrice quadrata di ordine 2:

$\displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}$

Vedi la soluzione

Dobbiamo innanzitutto determinare gli autovalori della matrice A. Calcoliamo quindi l’equazione caratteristica risolvendo il seguente determinante:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2$

Calcoliamo ora le radici del polinomio caratteristico:

$\displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}$

Una volta ottenuti gli autovalori si calcola l’autovettore associato a ciascuno. Innanzitutto, l’autovettore corrispondente all’autovalore -1:

$\displaystyle (A+I)v=0$

$\displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}$

E poi calcoliamo l’autovettore associato all’autovalore 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y$

$\displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}$

Costruiamo la matrice

$P$

, formato dagli autovettori della matrice:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}$

Poiché tutti gli autovalori sono diversi tra loro, la matrice A è diagonalizzabile. Quindi la matrice diagonale corrispondente è quella che contiene gli autovalori sulla diagonale principale:

$\displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Ricordare che gli autovalori devono essere posizionati nello stesso ordine in cui gli autovettori sono posizionati nella matrice

$P$

In conclusione, la matrice del cambiamento di base e la matrice diagonalizzata sono:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Esercizio 3

Diagonalizza la seguente matrice quadrata di dimensione 3×3:

$\displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}$

Vedi la soluzione

Il primo passo consiste nel trovare gli autovalori della matrice A. Calcoliamo quindi l’equazione caratteristica risolvendo il determinante della seguente matrice:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12$

Dobbiamo ora calcolare le radici del polinomio caratteristico. Trattandosi di un polinomio di terzo grado applichiamo la regola di Ruffini:

$\displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}$

E poi troviamo le radici del polinomio ottenuto:

$\displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}$

Quindi gli autovalori della matrice sono:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 4$

Una volta trovati gli autovalori si calcola l’autovettore associato a ciascuno di essi. Innanzitutto, l’autovettore corrispondente all’autovalore 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}$

Quindi calcoliamo l’autovettore associato all’autovalore 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

E infine, calcoliamo l’autovettore associato all’autovalore 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}$

Costruiamo la matrice

$P$

, formato dagli autovettori della matrice:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}$

Poiché tutti gli autovalori sono diversi tra loro, la matrice A è diagonalizzabile. Quindi la matrice diagonale corrispondente è quella che ha gli autovalori sulla diagonale principale:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Ricordare che gli autovalori devono essere posizionati nello stesso ordine in cui gli autovettori sono posizionati nella matrice

$P$

In breve, la matrice del cambiamento di base e la matrice diagonalizzata sono:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Esercizio 4

Diagonalizza, se possibile, la seguente matrice quadrata di ordine 3:

$\displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}$

Vedi la soluzione

Il primo passo consiste nel trovare gli autovalori della matrice A. Calcoliamo quindi l’equazione caratteristica risolvendo il determinante della seguente matrice:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8$

Dobbiamo ora calcolare le radici del polinomio minimo. Poiché si tratta di un polinomio di terzo grado, applichiamo la regola di Ruffini per fattorizzarlo:

$\displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}$

E poi troviamo le radici del polinomio ottenuto:

$\displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}$

Quindi gli autovalori della matrice sono:

$\lambda=2 \qquad \lambda =2 \qquad \lambda = -2$

L’autovalore di -2 è di molteplicità algebrica semplice, invece l’autovalore di 2 è di molteplicità doppia.

Una volta trovati gli autovalori si calcola l’autovettore associato a ciascuno di essi. Innanzitutto, l’autovettore corrispondente all’autovalore -2:

$\displaystyle (A+2I)v=0$

$\displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}$

Calcoliamo ora gli autovettori associati agli autovalori 2.

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}$

Poiché l’autovalore 2 viene ripetuto due volte, dobbiamo calcolare un altro autovettore che soddisfi le equazioni del sottospazio (o autospazio):

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}$

Costruiamo la matrice

$P$

, formato dai tre autovettori della matrice:

$\displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}$

Tuttavia i tre vettori non sono linearmente indipendenti, poiché ovviamente i due autovettori con autovalore 2 sono una combinazione lineare tra loro. Questo può anche essere dimostrato perché il determinante della matrice

$P$

è uguale a 0 (ha una riga piena di zeri):

$\displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0$

Pertanto, poiché gli autovettori sono linearmente dipendenti, la matrice A non è diagonalizzabile .

Esercizio 5

Se possibile, diagonalizza la seguente matrice quadrata di dimensione 3×3:

$\displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}$

Vedi la soluzione

Il primo passo consiste nel trovare gli autovalori della matrice A. Calcoliamo quindi l’equazione caratteristica risolvendo il determinante della seguente matrice:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}$

Poiché la prima riga è interamente composta da zeri tranne 3, ne approfitteremo per risolvere il determinante della matrice mediante cofattori (o aggiunti):

$\displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}$

Dobbiamo ora calcolare le radici del polinomio caratteristico. È meglio non moltiplicare le parentesi perché si otterrebbe un polinomio di terzo grado. Se invece i due fattori vengono risolti separatamente è più semplice ottenere gli autovalori:

$\displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}$

Quindi gli autovalori della matrice sono:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 3$

Una volta trovati gli autovalori si calcola l’autovettore associato a ciascuno di essi. Innanzitutto, l’autovettore corrispondente all’autovalore 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Successivamente calcoliamo gli autovettori associati agli autovalori 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}$

Poiché l’autovalore 3 viene ripetuto due volte, dobbiamo calcolare un altro autovettore che soddisfi le equazioni dell’autospazio:

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

Costruiamo la matrice

$P$

, formato dagli autovettori della matrice:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}$

A differenza dell’esercizio 4, in questo caso siamo riusciti a formare 3 vettori linearmente indipendenti sebbene la molteplicità algebrica dell’autovalore 3 sia doppia. Ciò può essere verificato vedendo che il determinante della matrice

$P$

dà un risultato diverso da 0:

$\displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0$

Possiamo così effettuare la scomposizione diagonale della matrice A. E la matrice diagonale corrispondente è quella che ha gli autovalori sulla diagonale principale:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Ricordare che gli autovalori devono essere posizionati nello stesso ordine in cui gli autovettori sono posizionati nella matrice

$P$

In breve, la matrice di cambiamento di base necessaria per diagonalizzare la matrice e la sua forma diagonalizzata sono:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Esercizio 6

Effettuare la diagonalizzazione, se possibile, della seguente matrice di dimensione 4×4:

$\displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Vedi la soluzione

Il primo passo consiste nel trovare gli autovalori della matrice A. Calcoliamo quindi l’equazione caratteristica risolvendo il determinante della seguente matrice:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}$

In questo caso l’ultima colonna del determinante è composta solo da zeri tranne un elemento, ne approfitteremo quindi per calcolare il determinante per cofattori tramite questa colonna:

$\displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}$

Dobbiamo ora calcolare le radici del polinomio caratteristico. È meglio non fare il prodotto tra parentesi perché altrimenti otterresti un polinomio di quarto grado. Tuttavia, se i due fattori vengono risolti separatamente, è più semplice calcolare gli autovalori:

$\displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}$

$\displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}$

Quindi gli autovalori della matrice sono:

$\lambda=0 \qquad \lambda =-3 \qquad \lambda = 2\qquad \lambda = 5$

Una volta trovati tutti gli autovalori si passa agli autovettori. Calcoliamo l’autovettore associato all’autovalore 0:

$\displaystyle (A-0I)v=0$

$\displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Calcoliamo l’autovettore associato all’autovalore -3:

$\displaystyle (A+3I)v=0$

$\displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Calcoliamo l’autovettore associato all’autovalore 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Calcoliamo l’autovettore associato all’autovalore 5:

$\displaystyle (A-5I)v=0$

$\displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}$

Realizziamo la matrice

$P$

, composto dagli autovettori della matrice:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}$

Poiché tutti gli autovalori sono diversi tra loro, la matrice A è diagonalizzabile. Quindi la matrice diagonale corrispondente è quella che ha gli autovalori sulla diagonale principale:

$\displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Ricordare che gli autovalori devono essere posizionati nello stesso ordine in cui sono posizionati gli autovettori nella matrice

$P$

In sintesi, le modifiche di base necessarie per diagonalizzare la matrice A e la matrice in forma diagonale sono:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Applicazioni di matrici diagonalizzabili

Se sei arrivato fin qui, probabilmente ti starai chiedendo: a cosa serve una matrice diagonalizzabile?

Ebbene, le matrici diagonalizzabili sono molto utili e ampiamente utilizzate in matematica. Il motivo è che una matrice diagonale è praticamente piena di zeri e quindi rende i calcoli molto più semplici.

Un chiaro esempio di ciò sono le potenze delle matrici diagonalizzabili, perché il loro risultato è semplificato dalla seguente formula:

$\displaystyle A^k=PD^kP^{-1}$

Questa uguaglianza può essere facilmente dimostrata per induzione. È quindi sufficiente innalzare la matrice

$D$

all’espositore. E poiché si tratta di una matrice diagonale, l’operazione si riduce ad elevare all’esponente ciascun termine della diagonale principale:

$\displaystyle D^k = diag(\lambda_1^k,\lambda_2^k, \ldots , \lambda_n^k)$

Esempio di potenza di una matrice diagonalizzabile

Per meglio comprendere, calcoleremo come esempio la potenza di una matrice diagonalizzabile:

$\displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}$

La matrice del cambiamento di base

$P$

, formato dai suoi autovettori, e dalla matrice diagonalizzata

$D$

, composto dai propri valori, sono:

$\displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}$

Quindi, per fare un esempio, la matrice A elevata a 7 equivale a:

$\displaystyle A^7=PD^7P^{-1}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}$

Ora invertiamo la matrice

$P:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

Risolviamo la potenza della matrice

$D:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

E, infine, effettuiamo le moltiplicazioni delle matrici:

$\displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}$

Come hai visto, è più conveniente calcolare la potenza con una matrice diagonale piuttosto che moltiplicare la stessa matrice sette volte di seguito. Quindi immagina con valori esponenti molto più grandi.

Proprietà delle matrici diagonalizzabili

Le caratteristiche di questo tipo di matrice sono:

Se la matrice
$A$

è diagonalizzabile, qualsiasi potenza di

$A$

.

Quasi tutte le matrici possono essere diagonalizzate in un ambiente complesso
$\mathbb{C}$

. Anche se di seguito hai le eccezioni che non sono mai diagonalizzabili.

Se la matrice
$P$

è una matrice ortogonale, allora diciamo che la matrice

$A$

è ortogonalmente diagonalizzabile e, quindi, l’equazione può essere riscritta:

$\displaystyle A=PDP^t$

Una matrice è diagonalizzabile da una matrice unitaria se e solo se è una matrice normale.

Date due matrici diagonalizzabili, esse sono commutabili se e solo se possono essere diagonalizzate simultaneamente, cioè se condividono la stessa base ortonormale di autovettori (o autovettori).

Se un endomorfismo è diagonalizzabile si dice che è diagonalizzabile per somiglianza . Tuttavia non tutti gli endomorfismi sono diagonalizzabili, ovvero la diagonalizzazione di un endomorfismo non è assicurata.

Diagonalizzazione simultanea

Un insieme di matrici si dice simultaneamente diagonalizzabile se esiste una matrice invertibile che serve come base per diagonalizzare qualsiasi matrice di questo insieme. In altre parole, se due matrici diagonalizzano sulla stessa base autovettoriale, significa che sono diagonalizzabili simultaneamente.

Inoltre, come abbiamo commentato nelle proprietà della diagonalizzazione delle matrici, se due matrici sono in grado di diagonalizzarsi simultaneamente, devono commutare tra loro.

Ad esempio, le seguenti due matrici sono commutabili, quindi diagonalizzano sulla stessa base di autovettori o autovettori.

$\displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}$

Anche se hanno gli stessi autovettori, ciò non significa che abbiano gli stessi autovalori. Infatti, sebbene le matrici A e B sopra abbiano autovettori simili, hanno autovalori diversi.

Matrici non diagonalizzabili

Sebbene la stragrande maggioranza delle matrici sia diagonalizzabile in un ambiente di numeri complessi, alcune matrici non possono mai essere diagonalizzabili.

Questo fatto si verifica quando la molteplicità algebrica di un autovalore (o autovalore) non coincide con la molteplicità geometrica.

Ad esempio, la seguente matrice non è in alcun modo diagonalizzabile, è “indiagonalizzabile”:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}$

Inoltre, ci sono matrici che non sono in grado di diagonalizzare in un ambiente di numeri reali, ma lo fanno quando si lavora con numeri complessi, come questa matrice:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}$

Infine, ci sono alcune procedure di diagonalizzazione dei blocchi di matrice che non sono puramente diagonalizzabili, ma sono un po’ più complicate. Il metodo più conosciuto è la diagonalizzazione con la forma canonica di Jordan .

Diagonalizzare una matrice con MATLAB

I programmi per computer sono molto utili quando si tratta di diagonalizzare matrici, soprattutto se sono molto grandi. E il software più conosciuto è sicuramente MATLAB , quindi di seguito vedremo come fattorizzare diagonalmente una matrice utilizzando questo programma.

L’istruzione utilizzata per diagonalizzare una matrice con MATLAB è:

$\displaystyle \text{[P, D] = eig(A)}$

Oro

$A$

è la matrice da diagonalizzare e

$P$

$D$

sono le matrici che il programma restituisce:

$P$

è la matrice formata dagli autovettori e

$D$

è la matrice in forma diagonale i cui termini diagonali principali sono gli autovalori.

Pertanto, devi solo inserire questo codice nel programma.

Se invece vuoi conoscere solo gli autovalori, puoi usare la seguente istruzione:

$\displaystyle e= eig(A)}$

Oro

$e$

è il vettore colonna che MATLAB restituisce con gli autovalori della matrice

$A$

Cos’è una matrice diagonalizzabile?

Quando puoi diagonalizzare una matrice?

Come diagonalizzare una matrice

Risolti gli esercizi di diagonalizzazione della matrice

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Applicazioni di matrici diagonalizzabili

Esempio di potenza di una matrice diagonalizzabile

Proprietà delle matrici diagonalizzabili

Diagonalizzazione simultanea

Matrici non diagonalizzabili

Diagonalizzare una matrice con MATLAB

Lascia un commento Annulla risposta