▷ Regola della catena (derivate): esercizi risolti

Qui imparerai cos’è la regola della catena e come derivare funzioni utilizzando la regola della catena. Inoltre, potrai vedere diversi esempi di derivate risolte con la regola della catena e potrai anche esercitarti con esercizi risolti passo dopo passo sulle derivate applicando la regola della catena.

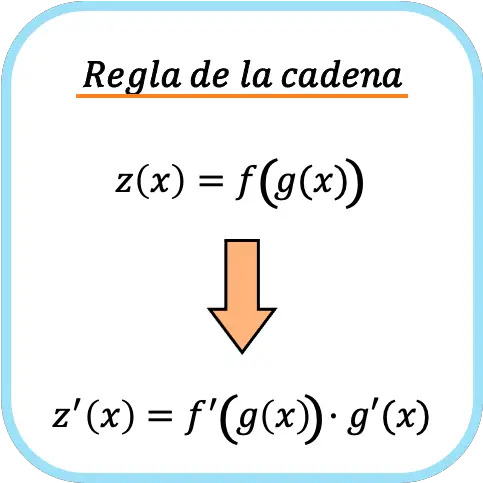
Qual è la regola della catena?

La regola della catena è una formula utilizzata per derivare funzioni composte. La regola della catena afferma che la derivata di una funzione composta f(g(x)) è uguale alla derivata f'(g(x)) moltiplicata per la derivata g'(x) .

➤ Vedi: funzione composita

Informalmente, si dice spesso che la regola della catena consista nel differenziare la funzione e quindi moltiplicarla per ciò che contiene .

La formula della regola della catena ci permette di differenziare le funzioni composte molto più facilmente, perché se dovessimo differenziare una composizione di funzioni utilizzando il limite della definizione di derivata, dovremmo fare molti calcoli.

D’altra parte bisogna tenere presente che questa regola viene utilizzata solo per trovare la derivata di funzioni composte e non di qualsiasi tipo di funzione o operazioni con funzioni. Ad esempio, un errore molto comune è sbagliare e applicare la regola della catena a prodotti funzionali come i seguenti:

$\ln(x)\cdot x^2$

❌

La regola della catena può essere utilizzata solo quando abbiamo una funzione all’interno di un’altra .

$\ln(x^2)$

✅

Esempi di derivate con la regola della catena

Data la definizione della regola della catena, deriveremo diverse funzioni prendendo come esempio la regola della catena. Ricorda che se in un esempio non capisci come si deriva la funzione con la regola della catena, puoi chiedercelo nei commenti!

Esempio 1

In questo esempio, utilizzeremo la regola della catena per ricavare il logaritmo naturale di x al quadrato:

$f(x)=\ln(x^2)$

La derivata del logaritmo naturale è pari a 1 volta il suo argomento, quindi la derivata

$f'\bigl(g(x)\bigr)$

Essere:

$f(x)=\ln(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{u}$

$f\bigl(g(x)\bigr)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\cfrac{1}{x^2}$

D’altra parte, la derivata di x elevata alla potenza di due è 2x:

$g(x)=x^2\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=2x$

Infine, calcoliamo la derivata dell’intera funzione applicando la regola della catena. La derivata della funzione composta sarà il prodotto delle due derivate che abbiamo appena trovato:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x^2}\cdot 2x = \cfrac{2x}{x^2}=\cfrac{2}{x}$

Esempio 2

In questo secondo esempio, deriveremo una funzione potenziale basata su un polinomio:

$f(x)=\left(3x^2+4x-5\right)^3$

Per derivare una potenza, dobbiamo anteporre l’esponente originale e sottrarre un’unità dall’esponente, quindi la derivata della funzione potenziale senza applicare la regola della catena sarebbe:

$f\bigl(g(x)\bigr)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=3\left(3x^2+4x-5\right)^2$

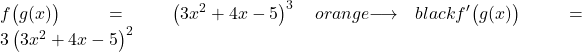
Ora deduciamo ciò che è tra parentesi:

$g(x)=3x^2+4x-5\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=6x+4$

Infine, utilizziamo la regola della catena per risolvere la derivata dell’intera funzione, che sarà la moltiplicazione delle due derivate calcolate in precedenza:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=3\left(3x^2+4x-5\right)^2\cdot (6x+4)$

Esempio 3

In questo caso, risolveremo la derivata seno di x al cubo più 7x:

$f(x)=\text{sen}(x^3+7x)$

Infatti è una composizione di funzioni perché abbiamo la funzione x ³ +7x all’interno della funzione seno, possiamo quindi usare la regola della catena per trovare la derivata della funzione composta.

Da un lato, la derivata del seno è il coseno, quindi la derivata della funzione esterna sarà il coseno con lo stesso argomento del seno:

$f\bigl(g(x)\bigr)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\text{cos}(x^3+7x)$

E d’altra parte, la derivata di x ³ +7x è 3x ² +7.

$g(x)=x^3+7x\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=3x^2+7$

Pertanto, la derivata della funzione composta è il prodotto delle due derivate:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cos}(x^3+7x)\cdot (3x^2+7)$

Risolti esercizi sulle derivate con la regola della catena

Esercizio 1

Derivare la seguente funzione composta utilizzando la regola della catena:

$f(x)=\left(5x^2-6x\right)^3$

Vedi la soluzione

La funzione esterna è una funzione potenziale, quindi per calcolarne la derivata è necessario applicare la seguente formula:

$f\bigl(g(x)\bigr)=a\bigl(g(x)\bigr)^n \ \longrightarrow \ f'\bigl(g(x)\bigr)=n\cdot a\bigl(g(x)\bigr)^{n-1}$

$f\bigl(g(x)\bigr)=\left(5x^2-6x\right)^3\ \longrightarrow \ f'\bigl(g(x)\bigr)= 3\left(5x^2-6x\right)^2$

E poi calcoliamo la derivata della funzione interna. È una sottrazione di potenze, quindi per calcolarne la derivata è necessario applicare a ciascuno dei suoi termini la seguente formula:

$f(x)=ax^n \ \longrightarrow \ f'(x)=n\cdot ax^{n-1}$

$g(x)=5x^2-6x\ \longrightarrow$

$g'(x)=2\cdot 5x^1-1 \cdot 6 x^0 =10x-6$

In breve, la derivata della funzione composta è il prodotto delle due derivate trovate:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(5x^2-6x\right)^3 \ \longrightarrow \ \bm{f'(x)= 3\left(5x^2-6x\right)^2\cdot (10x-6)}$

Esercizio 2

Risolvi la derivata della seguente funzione composta utilizzando la regola della catena:

$f(x)=-3\left(5x^5+9x^3\right)^4$

Vedi la soluzione

Per prima cosa troviamo la derivata della funzione esterna:

$\begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}$

E ora risolviamo la derivata della funzione interna:

$g(x)=5x^5+9x^3\ \longrightarrow \ g'(x)=25x^4+27x^2$

La derivata dell’intera funzione è quindi:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=-3\left(5x^5+9x^3\right)^4 \ \longrightarrow \ \bm{f'(x)=-12\left(5x^5+9x^3\right)^3\cdot \left(25x^4+27x^2\right)}$

Esercizio 3

Calcola la derivata della seguente composizione di funzioni con la regola della catena:

$f(x)=e^{2x^3}$

Vedi la soluzione

È una funzione esponenziale, quindi per calcolarne la derivata è necessario applicare la seguente formula:

$f(x)=e^{x} \ \longrightarrow \ f'(x)=e^{x}$

$f\bigl(g(x)\bigr)=e^{2x^3} \ \longrightarrow \ f'\bigl(g(x)\bigr)= e^{2x^3}$

Differenziamo anche la funzione dall’esponente della funzione:

$g(x)=2x^3 \ \longrightarrow \ g'(x)=6x^2$

E usiamo la regola della catena per trovare la derivata della funzione composta intera:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=e^{2x^3} \ \longrightarrow \ \bm{f'(x)= e^{2x^3}\cdot 6x^2}$

Esercizio 4

Trova la derivata della seguente funzione composta utilizzando la regola della catena:

$f(x)=\sqrt[3]{\text{sen}(x) +x }$

Vedi la soluzione

Questa è una composizione di funzioni, perché abbiamo una funzione sinusoidale e una funzione lineare nell’argomento di una funzione irrazionale. Quindi calcoliamo prima la derivata della radice:

$f(x)=\sqrt[n]{x} \ \longrightarrow \ f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

$f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}$

E ora deriviamo l’argomento dal radicale. È una somma di funzioni, quindi la derivata sarà la somma delle derivate di ciascun termine:

$g(x)=\text{sen}(x) +x \ \longrightarrow \ g'(x)=\cos(x) + 1$

Pertanto la derivata dell’intera funzione è uguale alla moltiplicazione delle due derivate calcolate:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}$

Esercizio 5

Derivare la seguente composizione di funzioni utilizzando la regola della catena:

$f(x)=3^{x^2+5}$

Vedi la soluzione

Per applicare la regola della catena, devi trovare la derivata della potenza e del polinomio e poi moltiplicarli. Pertanto, ricaviamo la potenza utilizzando la formula corrispondente:

$f(x)=a^x \ \longrightarrow \ f'(x)=a^x\cdot \ln (a)$

$f\bigl(g(x)\bigr)=3^{x^2+5} \ \longrightarrow \ f'\bigl(g(x)\bigr)= 3^{x^2+5}\cdot \ln(3)$

In secondo luogo, deriviamo la funzione polinomiale dall’esponente:

$g(x)=x^2+5 \ \longrightarrow \ g'(x)=2x$

E la regola della catena ci dice che la derivata dell’intera funzione è il prodotto delle derivate che abbiamo appena trovato:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=3^{x^2+5} \ \longrightarrow \ \bm{f'(x)= 3^{x^2+5}\cdot \ln(3) \cdot 2x}$

Esercizio 6

$f(x)=\ln \bigl(4x^2 \cdot \cos(x) \bigr)$

Vedi la soluzione

Ovviamente la funzione in questo problema è composita, poiché nell’argomento del logaritmo naturale abbiamo il prodotto di due diversi tipi di funzioni. Quindi differenziamo prima il logaritmo:

$f(x)=\ln(x) \ \longrightarrow \ f'(x)=\cfrac{1}{x}$

$f\bigl(g(x)\bigr)=\ln \bigl(4x^2 \cdot \cos(x) \bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{4x^2 \cdot \cos(x) }$

In secondo luogo, deriviamo la funzione dall’argomento logaritmo. Questa è una moltiplicazione di due funzioni, quindi è necessario utilizzare la seguente formula per eseguire la derivazione:

$z(x)=f(x) \cdot g(x) \ \longrightarrow \ z'(x)=f'(x)\cdot g(x)+f(x) \cdot g'(x)$

$\begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}$

Pertanto la derivata dell’intera funzione, secondo la regola della catena, sarà il prodotto delle due derivate:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}$

Esercizio 7

Risolvi la derivata della seguente funzione utilizzando la regola della catena:

$f(x)=\log_9 (e^{x^2}-6x^7)$

Vedi la soluzione

Questa è una composizione di funzioni, quindi differenzieremo separatamente il logaritmo e il suo argomento e poi moltiplicheremo le derivate.

Quindi, per prima cosa differenziamo il logaritmo in base 9:

$f(x)=\log_a (x) \ \longrightarrow \ f'(x)=\cfrac{1}{x\cdot \ln (a)}$

$f\bigl(g(x)\bigr)=\log_9 (e^{x^2}-6x^7) \ \longrightarrow \ f'\bigl(g(x)\bigr)=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}$

E ora calcoliamo la derivata dell’argomento del logaritmo. Nota che il numero e ha una funzione nel suo argomento, cioè è una funzione composta, quindi dobbiamo applicare anche la regola della catena per derivare questa funzione:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$h(x)=e^{x^2} \ \longrightarrow \ h'(x)=e^{x^2}\cdot \bigl(x^2\bigr)' =e^{x^2}\cdot 2x$

Pertanto, la derivata dell’argomento intero del logaritmo sarà:

$g(x)= e^{x^2}-6x^7\ \longrightarrow \ g'(x)=e^{x^2}\cdot 2x - 42x^6$

E infine, la derivata dell’intera funzione sarà il prodotto di f'(g(x)) e g'(x):

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}$

Esercizio 8

Derivare la seguente funzione composta utilizzando la regola della catena:

$f(x)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

Vedi la soluzione

In questo esercizio abbiamo una composizione di più funzioni, quindi dovremo applicare più volte la regola della catena. Per prima cosa deriviamo la funzione trigonometrica dal seno, la cui derivata è coseno:

$f\bigl(g(x)\bigr)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)\ \longrightarrow \ f'\bigl(g(x)\bigr)=\cos\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

E ora calcoliamo la derivata del seno usando la regola della catena:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}$

Infine, otteniamo la derivata dell’intera composizione delle funzioni applicando nuovamente la regola della catena:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\bm{f'(x)=\cos } \bm{\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr) \cdot 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-}\mathbf{sen}\bm{(x)\Bigr)}$

Prova della regola della catena

Infine, dimostreremo la formula della regola della catena. Per fare ciò, partiremo dalla definizione matematica di derivata:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Sia z una funzione composta da due funzioni:

$z=f\bigl(g(x)\bigr)$

Allora la derivata della funzione z applicando la definizione sarebbe:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}$

Come già sai, puoi moltiplicare e dividere una frazione per lo stesso termine, perché ciò non cambia il risultato. Possiamo quindi passare allo step successivo:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}\cdot \frac{g(x+h)-g(x)}{g(x+h)-g(x)}$

Riorganizziamo i denominatori delle frazioni:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \frac{g(x+h)-g(x)}{h}$

Applicando le proprietà dei limiti, possiamo dividere il limite di cui sopra in due. Poiché il limite di un prodotto è uguale al prodotto dei limiti:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

E questa espressione è equivalente alla seguente:

$\displaystyle z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

La formula della regola della catena è quindi dimostrata, poiché ad essa siamo arrivati dalla definizione della derivata.

Regola della catena (derivati)

Qual è la regola della catena?

Esempi di derivate con la regola della catena

Esempio 1

Esempio 2

Esempio 3

Risolti esercizi sulle derivate con la regola della catena

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Esercizio 7

Esercizio 8

Prova della regola della catena

Lascia un commento Annulla risposta