Binomi - Mathority

In questa pagina troverai una spiegazione di cos’è un binomio e, inoltre, potrai vedere esempi di ogni tipo di binomio. Inoltre, ti mostriamo le formule utilizzate per risolvere le operazioni con i binomi: moltiplicazione di binomi, binomio al quadrato, binomio al cubo,…

Cos’è una coppia?

In algebra, la definizione di binomio è:

Un binomio è un polinomio composto da soli due monomi . In altre parole, un binomio è costituito da un’espressione algebrica con solo 2 termini diversi uniti dal segno più (+) o dal segno meno (-).

La parola binomio deriva dal greco ed è composta da due componenti lessicali ( bi e nomos ), che significano quanto segue:

bi : prefisso che significa 2.
nomos : significa parte.

Possiamo quindi dedurre il significato del binomio: polinomio con due parti (o 2 monomi).

D’altronde il concetto di coppia ha un significato diverso da quello matematico, e cioè che una coppia può designare anche un insieme di due personalità che hanno un ruolo di primo piano nella vita politica, in alcune discipline sportive o anche nello spettacolo. . Ma qui ci concentreremo ovviamente sulla definizione matematica del binomio.

Esempi di binomi

Per finire di comprendere la nozione di binomio, vedremo diversi esempi di questo tipo di polinomio:

Esempio di binomio quadratico:

$x^2+4x$

Esempio di binomio di terzo grado:

$x^3+5$

Esempio di binomio di quarto grado:

$3x^4+8x^2$

Ora che sappiamo cos’è un binomio, vedremo i diversi tipi di binomi che esistono e come si risolvono le operazioni con i binomi.

binomio quadrato

Un binomio quadrato è un’identità notevole, chiamata anche prodotto notevole o uguaglianza notevole. Risolvere la potenza di un binomio elevato a 2 dipende dal fatto che si tratti di un binomio somma o differenza.

Un binomio somma si riferisce a quel binomio i cui due termini sono positivi, vale a dire un binomio somma quadrata è:

$(a+b)^2$

D’altra parte, un binomio di differenza (o sottrazione) è il coniugato del binomio di addizione, vale a dire che uno dei suoi monomi ha segno negativo. Pertanto, l’espressione algebrica per una differenza binomiale quadrata è:

$(a-b)^2$

Per calcolare un binomio quadrato bisogna applicare una formula che, come abbiamo visto, varia a seconda che si tratti di un’addizione o di una sottrazione. Scopri come si fa nelleformule per le uguaglianze notevoli , dove puoi vedere tutte le spiegazioni passo passo, nonché esempi ed esercizi risolti, e non solo di queste 2 uguaglianze notevoli ma di tutte.

binomio al cubo

Anche se usati meno spesso, anche i binomi cubici sono considerati prodotti degni di nota. O in altre parole, esistono delle regole matematiche che permettono di trovare velocemente il cubo di un binomio (puoi vederle nel link sopra delle formule delle identità notevoli ).

Come prima, il risultato di questo potenziamento dipende dal fatto che sia il cubo di una somma:

$(a+b)^3$

O se, al contrario, la potenza è costituita dal cubo di una differenza o di una sottrazione:

$(a-b)^3$

Logicamente, la differenza principale tra un binomio al quadrato e un binomio al cubo è l’esponente della potenza. Tuttavia, la formula per un binomio al cubo è molto più complicata di quella per un binomio al quadrato.

accordi notevoli

Esistono in particolare alcuni tipi di binomi che sono un po’ particolari per le loro caratteristiche, poiché corrispondono a identità notevoli (o prodotti notevoli) meno conosciute.

Somma dei quadrati:
$a^2+b^2$
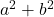
Differenza (o sottrazione) di quadrati:
$a^2-b^2$
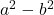
Somma dei cubi:
$a^3+b^3$
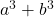
Differenza (o sottrazione) di cubi:
$a^3-b^3$

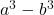
Oro

$a$

$b$

sono due monomi qualsiasi.

Sebbene queste espressioni binomiali assomiglino molto a quelle che abbiamo visto appena sopra (binomio al quadrato e binomio al cubo), se guardi da vicino sono diverse. In questo senso, puoi anche vedere le formule dei binomi notevoli e le loro deduzioni cliccando sul link qui sopra ⬆ formule di identità notevoli.⬆

moltiplicazione binomiale

Una delle operazioni più comuni con i binomi è la moltiplicazione. Quindi di seguito vedremo un esempio di come calcolare una moltiplicazione tra binomi.

$(x^2+2x)\cdot (x-5)$

Per calcolare la moltiplicazione binomiale, dobbiamo prima moltiplicare ciascun termine del primo binomio per ciascun termine del secondo binomio:

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

Successivamente raggruppiamo termini simili, cioè hanno la stessa parte letterale:

$\bm{x^3-3x^2 -10x}$

E in questo modo siamo riusciti a trovare il risultato del prodotto tra le coppie.

Prodotto di due binomi con un termine comune

Quando i binomi che partecipano alla moltiplicazione hanno come termine comune la variabile

$x,$

Esiste una formula per calcolare rapidamente questa operazione binomiale:

$(x+a)(x+b) = x^2+(a+b)x+ab$

Qui ti mostriamo un esercizio risolto in modo che tu possa vedere come applicare questa formula:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

Il binomio di Newton

Il binomio di Newton , chiamato anche teorema del binomio, è una formula utilizzata per calcolare le potenze dei binomi.

La formula matematica per il binomio di Newton è la seguente:

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

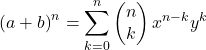
O equivalente:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

Come puoi vedere, questa formula è un po’ complessa da capire. Questo è il motivo per cui abbiamo riportato di seguito le potenze dei binomi di grado più basso in modo che tu possa capirle meglio:

formula per il teorema binomiale di Newton

Questa formula può essere un po’ noiosa per calcolare binomi al quadrato o al cubo, poiché, come abbiamo visto sopra, esistono formule più semplici. Tuttavia, il binomio di Newton è molto utile per trovare potenze di grado superiore, ad esempio è ampiamente utilizzato per determinare un binomio alla quarta.

Ma per applicare questa formula bisogna saper calcolare un numero combinatorio, cioè l’espressione algebrica del tipo

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

, calcolo non facile. 🔍 Per questo ti consigliamo di cercare come si fa nel nostro motore di ricerca in alto a destra 🔎, troverai il nostro articolo in cui ti spieghiamo passo dopo passo questa operazione.