Qui troverai quali sono gli asintoti verticali di una funzione (con esempi). Ti spieghiamo anche come trovare gli asintoti verticali di una funzione e, inoltre, potrai esercitarti con esercizi risolti passo dopo passo.
Cos’è un asintoto verticale?
Un asintoto verticale di una funzione è una linea verticale il cui grafico si avvicina indefinitamente senza mai attraversarlo. Pertanto, l’equazione per un asintoto verticale è x=k , dove k è il valore dell’asintoto verticale.
Cioè, k è un asintoto verticale se il limite della funzione quando x si avvicina a k è infinito.
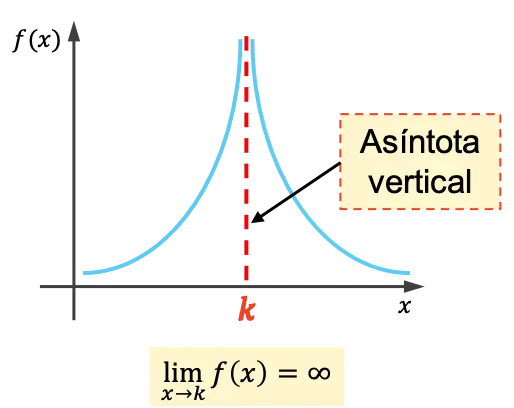
Come calcolare l’asintoto verticale di una funzione
Per calcolare l’asintoto verticale di una funzione è necessario seguire i seguenti passaggi:
- Trova il dominio della funzione. Se tutti i punti appartengono al dominio la funzione non ha asintoti verticali.
- Calcolare il limite della funzione nei punti che non appartengono al dominio.
- Gli asintoti verticali della funzione saranno tutti i valori in cui il limite dà infinito.
Tieni presente che una funzione può avere più di un asintoto verticale. Ad esempio, il grafico della funzione tangente ha infiniti asintoti verticali.
➤ Vedi: caratteristiche della funzione tangente
Esempio di asintoto verticale
Ad esempio, troveremo tutti gli asintoti della seguente funzione razionale in modo da poter vedere come si fa:
![]()
In generale i punti in cui sono presenti asintoti verticali non appartengono al dominio della funzione. Pertanto, calcoleremo prima il dominio della funzione.
È una funzione razionale, quindi guardiamo quando il denominatore svanisce per determinare i punti che non appartengono al dominio:
![]()
![]()
Pertanto, il dominio della funzione è costituito da tutti i numeri reali tranne x=2:
![]()
Quindi x=2 potrebbe essere un asintoto verticale della funzione. Per verificarlo dobbiamo calcolare il limite della funzione a questo punto:
![]()
In questo caso abbiamo ottenuto l’indeterminazione di un numero compreso tra zero e, quindi, per risolvere il limite dobbiamo calcolare i limiti laterali per sapere se è più infinito, meno infinito o se il limite non esiste. Tuttavia, quando calcoliamo gli asintoti verticali, non abbiamo bisogno di fare i limiti laterali, ma ottenere questa indeterminazione è sufficiente per dire che si tratta di un asintoto verticale.
In breve, poiché il limite della funzione quando x tende a 2 dà infinito, x=2 è un asintoto verticale.
Di seguito la funzione rappresentata graficamente. Come puoi vedere, si avvicina molto alla retta x=2 (sia da sinistra che da destra) ma non la interseca mai perché è un asintoto verticale:

Inoltre dal grafico si deducono i limiti laterali della funzione nel punto x=2:
![]()
Risolti problemi degli asintoti verticali
Esercizio 1
Calcolare l’asintoto verticale della seguente funzione razionale:
![]()
Non esiste una formula per calcolare gli asintoti verticali di una funzione, ma bisogna trovare il dominio della funzione e vedere in quali punti in cui la funzione non è definita il limite dà infinito.
Pertanto, poniamo il denominatore della funzione razionale uguale a 0 per trovare i punti che non appartengono al dominio:
![]()
![]()
![]()
Pertanto, il dominio della funzione è costituito da tutti i numeri reali tranne x=1/2:
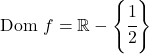
Quindi x=1/2 potrebbe essere un asintoto verticale. Per verificarlo, calcoliamo il limite della funzione a questo punto:
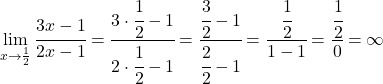
Quindi x=1/2 è un asintoto verticale , poiché il limite della funzione in questo punto dà infinito.
Esercizio 2
Trova tutti gli asintoti verticali della seguente funzione frazionaria:
![]()
Per prima cosa impostiamo il denominatore della frazione uguale a zero per vedere quali valori non rientrano nel dominio della funzione:
![]()
Risolviamo l’equazione quadratica incompleta:
![]()
![]()
Il dominio della funzione razionale è quindi:
![]()
Quindi, per determinare quali di questi due valori sono asintoti verticali, risolviamo il limite della funzione in ogni punto:
![]()
![]()
I due limiti danno infinito, quindi x=3 e x=-3 sono i due asintoti verticali della funzione problematica .
Esercizio 3
Trova, se li hai, tutti gli asintoti verticali della seguente funzione razionale:
![]()
➤ Vedi: zero tra zero indeterminatezza
Innanzitutto, risolviamo l’equazione del denominatore quadratico per trovare i valori che annullano il denominatore della frazione:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b2170358d5d1719077695aba5afa02e_l3.png)
Quindi il dominio della funzione è:
![]()
Quindi, calcoliamo prima il limite della funzione in x=1:
![]()
E invece risolviamo il limite della funzione quando x tende a -3:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0e96a48986cd110e04058e3545290a0_l3.png)
Il limite precedente dà la forma indeterminata zero tra zero, quindi per risolverlo dobbiamo fattorizzare i polinomi. Se hai qualche dubbio su come abbiamo risolto il limite, puoi vedere la spiegazione completa di come risolvere questo tipo di indeterminatezza nel link alla dichiarazione dell’esercizio.
In questo caso, solo il limite della funzione nel punto x=1 dà infinito, quindi x=1 è l’unico asintoto verticale della funzione .