Asintoto orizzontale

In questo articolo spieghiamo cosa sono gli asintoti orizzontali di una funzione e come si calcolano. Inoltre, troverai diversi esempi di questo tipo di asintoti per comprendere appieno il concetto e, inoltre, potrai esercitarti con esercizi risolti di asintoti orizzontali.

Cos’è un asintoto orizzontale?

Un asintoto orizzontale di una funzione è una linea orizzontale alla quale il suo grafico si avvicina indefinitamente senza mai incrociarla. Pertanto, l’equazione per un asintoto orizzontale è y=k , dove k è il valore dell’asintoto orizzontale.

Cioè, k è un asintoto orizzontale se il limite della funzione quando x tende all’infinito è uguale a k .

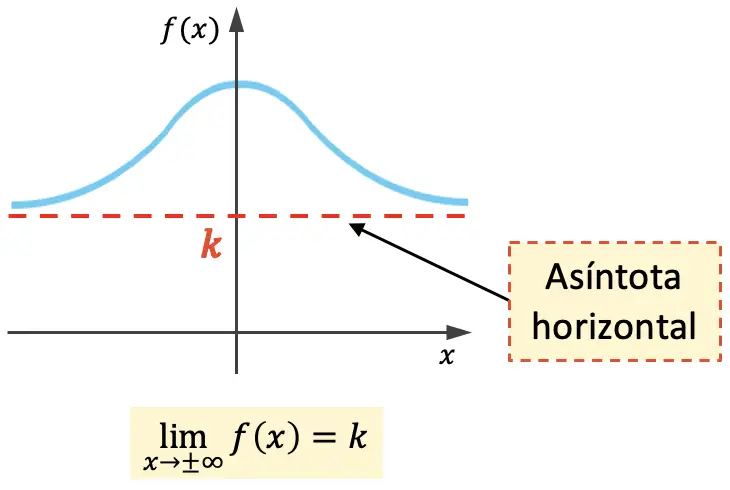
asintoto orizzontale di una funzione

La funzione sopra ha un asintoto orizzontale su entrambi i lati del grafico, ma una funzione può avere un asintoto orizzontale solo su un lato:

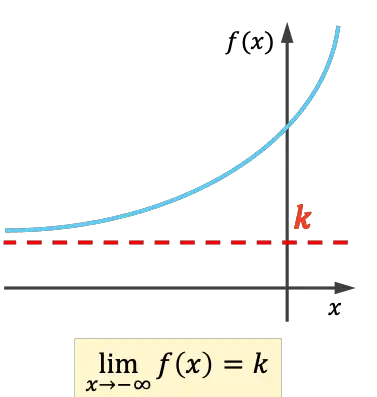
  • La funzione ha un asintoto orizzontale sinistro se il limite almeno all’infinito dà un numero reale.
  • La funzione ha un asintoto orizzontale a destra se il limite a più infinito dà un numero reale.
asintoto orizzontale di una funzione da sinistra
asintoto orizzontale a destra

Come calcolare l’asintoto orizzontale di una funzione

Per calcolare l’asintoto orizzontale di una funzione è necessario seguire i seguenti passaggi:

  1. Calcola il limite della funzione agli infiniti (+∞ e -∞).
  2. Se un limite all’infinito dà un numero reale (k), la linea y=k è un asintoto orizzontale della funzione.
  3. Se nessuno dei due limiti corrisponde a un numero reale, la funzione non ha asintoti orizzontali.

Esempio di asintoto orizzontale

Per vedere un esempio di come farlo, rimuoveremo tutti gli asintoti orizzontali dalla seguente funzione razionale:

f(x)=\cfrac{x+1}{x-1}

Per determinare gli asintoti orizzontali è necessario calcolare il limite a meno infinito e a più infinito della funzione:

\displaystyle \lim_{x \to +\infty} \cfrac{x+1}{x-1} = \cfrac{+\infty}{+\infty}= \cfrac{1}{1} = \bm{1}

\displaystyle \lim_{x \to -\infty} \cfrac{x+1}{x-1} = \cfrac{-\infty}{-\infty}= \cfrac{1}{1} = \bm{1}

➤ Vedi: come risolvere l’infinita indeterminazione tra infiniti

I due limiti all’infinito danno 1, quindi y=1 è l’unico asintoto orizzontale della funzione.

Di seguito la funzione rappresentata graficamente. Come puoi vedere, la funzione si avvicina molto a y=1 (sia a più infinito che a meno infinito), ma non lo tocca mai perché è un asintoto orizzontale.

esempio di asintoto orizzontale

Nota: in alcuni casi particolari la funzione interseca l’asintoto orizzontale in uno o più punti, ma in generale il grafico di una funzione non ne incrocia mai gli asintoti.

D’altra parte, questa funzione ha anche un asintoto verticale in x=1. Perché, come puoi vedere dal grafico, si avvicina molto alla linea x=1 ma non raggiunge mai quel valore.

Risolti problemi di asintoti orizzontali

Esercizio 1

Trova l’asintoto orizzontale, se presente, della seguente funzione frazionaria:

\displaystyle f(x)= \frac{4x+3}{2x-1}

Per determinare gli asintoti orizzontali della funzione razionale è necessario calcolare i limiti all’infinito della funzione:

\displaystyle \lim_{x \to +\infty} \frac{4x+3}{2x-1} = \frac{4(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{4}{2} = \bm{2}

\displaystyle \lim_{x \to -\infty} \frac{4x+3}{2x-1} = \frac{4(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{4}{2} = \bm{2}

In questo caso il risultato della forma indeterminata ∞/∞ è la divisione dei coefficienti delle x di grado massimo, poiché numeratore e denominatore sono dello stesso ordine.

I limiti a più infinito e meno infinito della funzione danno 2, quindi y=2 è un asintoto orizzontale ed è l’unico che la funzione ha.

Esercizio 2

Trova tutti gli asintoti orizzontali della seguente funzione razionale con una radice:

\displaystyle f(x)= \frac{3x}{\sqrt{x^2+2}}

Per trovare gli asintoti orizzontali della funzione, calcoliamo prima il limite all’infinito positivo:

\displaystyle \lim_{x \to +\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{+\infty}{+\infty} = \frac{3}{\sqrt{1}} = \bm{3}

E poi risolviamo il limite della funzione all’infinito negativo:

\displaystyle \lim_{x \to -\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{-\infty}{+\infty} = \frac{-3}{\sqrt{1}} = \bm{-3}

➤ Se hai dubbi su come sono stati risolti i limiti all’infinito, ti consigliamo di controllare il link qui sopra su come risolvere l’indeterminazione infinita tra l’infinito.

In questo caso abbiamo ottenuto due diversi valori dei limiti all’infinito. La funzione ha quindi due asintoti orizzontali: y=3 è un asintoto orizzontale della funzione di destra e, invece, y=-3 è un asintoto orizzontale della funzione di sinistra.

Esercizio 3

Calcolare gli asintoti orizzontali della seguente funzione definita a tratti:

\displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.

Per calcolare gli asintoti orizzontali della funzione non esiste una formula, ma è necessario calcolare i limiti al più e al meno infinito.

Pertanto, per trovare il limite almeno infinito, prendiamo la funzione definita nella prima sezione:

\displaystyle \lim_{x \to -\infty}\frac{3x-1}{x^2}= \frac{-\infty}{+\infty}=\bm{0}

Pertanto la linea y=0 è un asintoto orizzontale a sinistra della funzione.

E ora calcoliamo il limite a più infinito prendendo la funzione definita nella seconda sezione:

\displaystyle \lim_{x \to +\infty}\frac{x^3-2x+5}{2x^3-9}= \frac{+\infty}{+\infty}=\mathbf{\frac{1}{2}}

Pertanto la linea y=1/2 è un asintoto orizzontale a destra della funzione.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto