▷ Asintoto obliquo di una funzione (esercizi risolti)

In questo articolo spieghiamo cosa sono gli asintoti obliqui di una funzione. Imparerai quando una funzione ha un asintoto obliquo e come viene calcolato. Inoltre, potrai vedere esempi di asintoti obliqui ed esercitarti con esercizi risolti passo dopo passo.

Cos’è un asintoto obliquo?

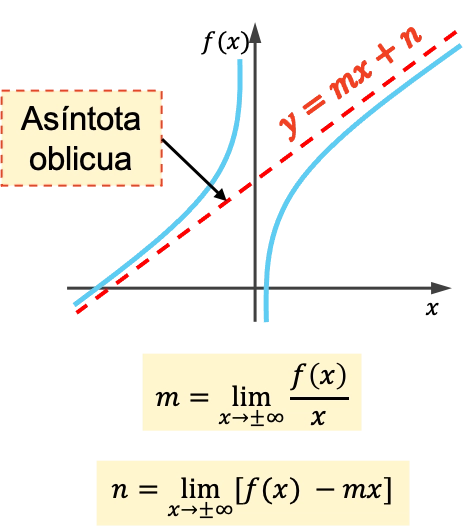
L’asintoto obliquo di una funzione è una linea inclinata alla quale il suo grafico si avvicina indefinitamente senza mai incrociarla. Di conseguenza, tutti gli asintoti obliqui sono linee con l’equazione y=mx+n .

La pendenza e l’origine di un asintoto obliquo si calcolano utilizzando le seguenti formule:

Come calcolare l’asintoto obliquo di una funzione

Per calcolare l’asintoto obliquo di una funzione è necessario eseguire i seguenti passaggi:

Calcola il limite all’infinito della funzione divisa per x.
Se il limite sopra indicato dà come risultato un numero reale diverso da zero, significa che la funzione ha un asintoto obliquo. Inoltre, la pendenza di detto asintoto obliquo sarà il valore ottenuto al limite.

$\displaystyle m = \lim_{x \to \pm\infty}\frac{f(x)}{x}$

In questo caso non resta che calcolare l’intercetta dell’asintoto obliquo risolvendo il seguente limite:

$\displaystyle n = \lim_{x \to \pm\infty} [f(x)-mx]$

Nota: i limiti vanno calcolati a più e meno infinito, ma normalmente danno lo stesso risultato ed è per questo che semplifichiamo mettendo ±∞. Ma se i limiti al più e al meno infinito fossero diversi, l’asintoto obliquo sinistro e l’asintoto obliquo destro dovrebbero essere calcolati separatamente.

Esempio di asintoto obliquo

Successivamente, prenderemo l’asintoto obliquo della seguente funzione razionale in modo da poter vedere un esempio di come viene eseguito:

$f(x)=\cfrac{x^2+1}{x}$

Gli asintoti obliqui sono del tipo

$y=mx+n.$

Quindi calcoliamo prima la pendenza della retta

$m$

con la relativa formula:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}$

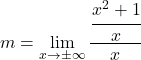
Per risolvere questo limite dobbiamo applicare le proprietà delle frazioni:

$\cfrac{\cfrac{a}{b}}{\cfrac{c}{d}}=\cfrac{a\cdot d}{b\cdot c}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}=\lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2}$

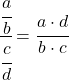
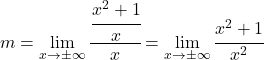
E ora calcoliamo il limite:

$\displaystyle m = \lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2} = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = \bm{1}$

In questo caso, il risultato dell’indeterminazione dell’infinito tra infiniti è la divisione dei coefficienti di x del grado più alto, poiché numeratore e denominatore sono dello stesso ordine.

Il limite sopra fornisce un numero reale diverso da zero, quindi la funzione ha un asintoto obliquo. Ora calcoleremo l’intercetta y

$n$

dell’asintoto utilizzando la formula corrispondente:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right]$

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]$

Proviamo a calcolare il limite:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Ma otteniamo l’indeterminazione infinito meno infinito. È quindi necessario ridurre i termini ad un denominatore comune. Per fare ciò, moltiplichiamo e dividiamo la x per il denominatore della frazione:

$\displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]$

Ora che i due termini hanno lo stesso denominatore possiamo raggrupparli:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}$

Operiamo sul numeratore:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}$

E infine, risolviamo il limite:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}= \cfrac{1}{\pm\infty} = \bm{0}$

Quindi n = 0. Pertanto, l’asintoto obliquo è una funzione lineare:

$y = mx+n$

$y = 1x+0$

$\bm{y=x}$

La funzione studiata è rappresentata nel grafico sottostante. Come puoi vedere, la funzione si avvicina molto alla retta y=x ma non la tocca mai perché è un asintoto obliquo:

Esercizi risolti sugli asintoti obliqui

Esercizio 1

Trova l’asintoto obliquo della seguente funzione razionale:

$\displaystyle f(x)= \frac{x^2+2x+3}{x+1}$

Vedi la soluzione

Gli asintoti obliqui sono della forma

$y=mx+n$

, è quindi necessario calcolare i parametri m e n . Per prima cosa calcoliamo m applicando la sua formula:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+2x+3}{x+1}}{x}$

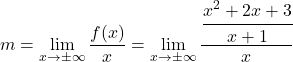
Semplifichiamo la frazione applicando le proprietà delle frazioni:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{(x+1)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}$

E risolviamo il limite:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}= \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Quindi m = 1. Calcoliamo ora l’intercetta dell’asintoto obliquo applicando la sua formula:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-1x\right]$

Proviamo a calcolare il limite:

$\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right]= \bm{+\infty - \infty}$

Ma otteniamo la forma indeterminata infinito meno infinito. Dobbiamo quindi ridurre i termini ad un denominatore comune e poi raggrupparli:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}$

E infine, risolviamo il limite:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{x+3}{x+1} = \frac{\infty}{\infty} = \frac{1}{1} = \bm{1}$

In breve, l’asintoto obliquo della funzione è:

$y = mx+n$

$y = 1x + 1$

$\bm{y = x + 1}$

Esercizio 2

Trova tutti gli asintoti obliqui della seguente funzione razionale:

$\displaystyle f(x)=\frac{2x^2-5}{x+3}$

Vedi la soluzione

Per prima cosa usiamo la formula per la pendenza dell’asintoto obliquo:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{2x^2-5}{x+3}}{x}$

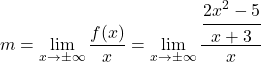
Semplifichiamo la frazione applicando le proprietà delle frazioni:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{(x+3)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}$

E determiniamo il limite:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}= \frac{+\infty}{+\infty} = \frac{2}{1} = \bm{2}$

Il limite dà un numero reale diverso da zero, quindi è una funzione razionale con asintoto obliquo la cui pendenza è 2.

Ora calcoliamo l’intercetta applicando la formula corrispondente:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]$

Proviamo a calcolare il limite:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]= \bm{+\infty - \infty}$

Ma otteniamo la differenza di indeterminatezza degli infiniti. Riduciamo quindi i termini ad un denominatore comune e poi operiamo:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}$

E infine, risolviamo il limite:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{-6x-5}{x+3}= \frac{\infty}{\infty}=\frac{-6}{1} = \bm{-6}$

In sintesi, l’asintoto obliquo della funzione frazionaria è:

$y = mx+n$

$\bm{y=2x-6}$

Cos’è un asintoto obliquo?

Come calcolare l’asintoto obliquo di una funzione

Esempio di asintoto obliquo

Esercizi risolti sugli asintoti obliqui

Esercizio 1

Esercizio 2

Lascia un commento Annulla risposta