Angolo tra una retta e un piano

Qui troverai come viene calcolato l’angolo tra una linea e un piano. Potrai anche vedere esempi e, inoltre, esercitarti con esercizi risolti passo dopo passo sugli angoli tra linee e piani.

Qual è l’angolo tra una linea e un piano?

L’angolo tra una linea e un piano è l’angolo tra la linea e la sua proiezione ortogonale sul piano.

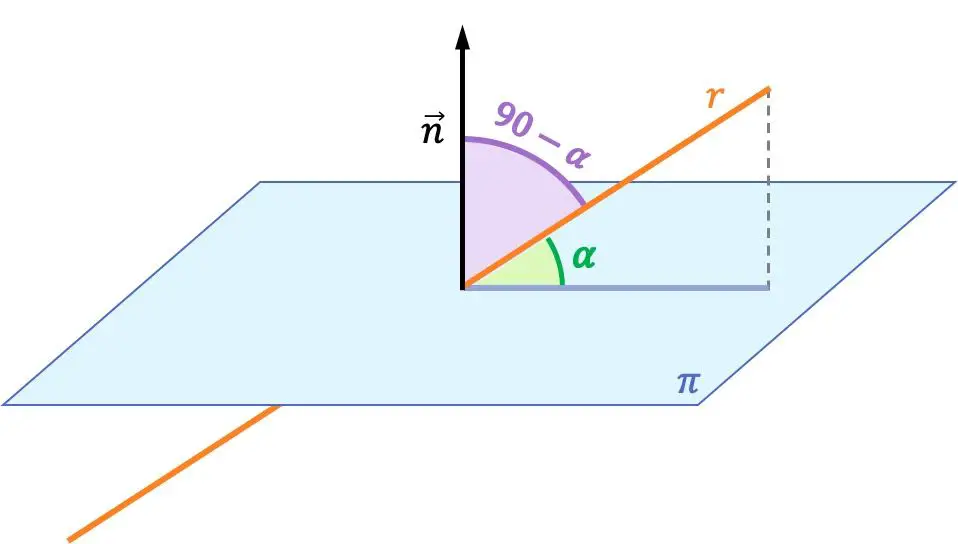
L’angolo tra una linea e un piano è il complementare dell’angolo tra detta linea e il vettore normale al piano. Pertanto, l’angolo tra una linea e un piano viene calcolato dall’angolo tra il vettore direzione della linea e il vettore normale del piano.

Formula dell’angolo tra una retta e un piano

Per dedurre la formula dell’angolo tra un piano e una linea, devi sapere come trovare l’angolo tra due vettori . Nella pagina collegata troverai la spiegazione oltre ad esempi ed esercizi risolti passo dopo passo, quindi se non ricordi come si fa ti consigliamo di dare un’occhiata.

Pertanto, poiché l’angolo tra una linea e un piano è complementare all’angolo tra il vettore direzione di detta linea

$(\vv{\text{v}}_r)$

e il vettore normale a detto piano

$(\vv{n})$

, dalla formula dell’angolo tra due vettori si deduce che l’angolo tra una retta ed un piano equivale alla seguente espressione:

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Pertanto la formula per calcolare l’angolo tra una linea e un piano è :

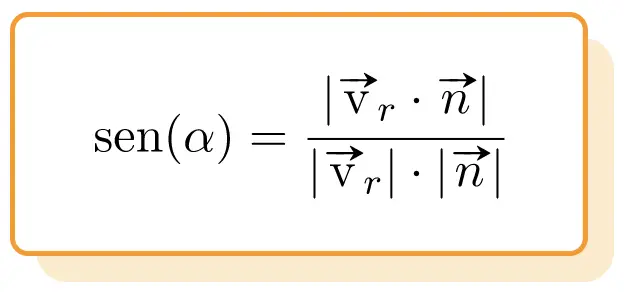
Oro:

$\vv{\text{v}}_r$

è il vettore diretto della retta.
$\vv{n}$

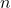
è il vettore normale al piano.

Esempio di calcolo dell’angolo tra una linea e un piano

Per capire come risolvere questo tipo di problema, ecco un esempio di calcolo dell’angolo tra una linea e un piano:

Calcola l’angolo formato dalla linea
$r$

con l’aereo

$\pi.$

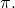
Lasciamo che le loro equazioni siano:

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

La linea è espressa sotto forma di equazioni parametriche, quindi il suo vettore direzione è:

$\vv{\text{v}}_r = (-1,4,-3)$

D’altra parte, il piano è definito sotto forma di un’equazione implicita (o generale), quindi il suo vettore normale è:

$\vv{n} = (1,-1,4)$

Pertanto, una volta conosciuto il vettore direzione della linea e il vettore normale del piano, applichiamo la formula per l’angolo tra una linea e un piano:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Sostituiamo i vettori nella formula:

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

E facciamo i calcoli:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

Infine invertiamo il seno con la calcolatrice e troviamo il valore dell’angolo:

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

L’angolo tra la linea e il piano è quindi di circa 51,80º.

Dobbiamo tenere presente che se mai otteniamo un risultato pari a 0º, ciò significa che la linea e il piano sono paralleli o che la linea è contenuta nel piano. E se l’angolo è uguale a 90º, ciò implica che la linea e il piano sono perpendicolari.

Risolti problemi dell’angolo tra una linea e un piano

Esercizio 1

Trova l’angolo formato dalla linea

$r$

con l’aereo

$\pi.$

Lasciamo che le loro equazioni siano:

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

vedi soluzione

La linea è espressa come un’equazione continua, quindi il suo vettore direzione è:

$\vv{\text{v}}_r = (2,-1,-3)$

D’altra parte, il piano ha la forma di un’equazione implicita (o generale), quindi il suo vettore normale è:

$\vv{n} = (3,1,2)$

Quindi, una volta conosciuto il vettore direzione della linea e il vettore normale del piano, usiamo la formula per l’angolo tra una linea e un piano:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

Infine invertiamo il seno e troviamo il valore dell’angolo:

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

Pertanto, l’angolo tra la linea e il piano è 4,10º.

Esercizio 2

Determina l’angolo formato dalla linea

$r$

con l’aereo

$\pi.$

Lasciamo che le loro equazioni siano:

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

vedi soluzione

La retta si esprime con le sue equazioni implicite (o generali), è quindi necessario trovare il vettore direzione della retta calcolando il prodotto vettoriale dei vettori normali ai 2 piani che determinano la retta:

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

D’altra parte, il vettore normale al piano è:

$\vv{n} = (-4,2,0)$

Quindi, una volta conosciuto il vettore direzione della linea e il vettore normale del piano, usiamo la formula per l’angolo tra una linea e un piano:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

Infine invertiamo il seno e troviamo il valore dell’angolo:

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

Pertanto, l’angolo tra la linea e il piano è 46,33º.

Esercizio 3

Trova, utilizzando la formula dell’angolo tra una linea e un piano, il valore di

$k$

necessario per il diritto

$r$

e l’aereo

$\pi$

essere parallelo.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

vedi soluzione

Innanzitutto, la linea è espressa come un’equazione vettoriale, quindi il suo vettore di direzione è:

$\vv{\text{v}}_r = (4,-1,3)$

D’altra parte, l’aereo ha la forma di un’equazione generale, quindi il suo vettore normale è:

$\vv{n} = (4,3,k)$

Quindi, affinché i due elementi geometrici siano paralleli, l’angolo tra loro deve essere zero. Pertanto, la formula per l’angolo tra una linea e un piano è:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

Pertanto, il prodotto scalare tra il vettore di direzione della linea e il vettore normale deve essere zero. E da questa equazione possiamo determinare il valore dell’incognita

$k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

Infine, se hai trovato utile questo articolo, probabilmente ti interesserà anche come trovare l’ angolo tra due piani . Nella pagina dei link troverai una spiegazione molto dettagliata nonché la formula necessaria per calcolare l’angolo tra due piani diversi e, inoltre, potrai vedere esempi ed esercizi risolti passo dopo passo per poter esercitarti e capire come è fatto perfettamente.

Angolo tra una linea e un piano

Qual è l’angolo tra una linea e un piano?

Formula dell’angolo tra una retta e un piano

Esempio di calcolo dell’angolo tra una linea e un piano

Risolti problemi dell’angolo tra una linea e un piano

Esercizio 1

Esercizio 2

Esercizio 3

Lascia un commento Annulla risposta