Angolo tra due linee (formula)

In questa pagina troverai la spiegazione di come calcolare l’angolo tra due linee (formula). Potrai anche vedere diversi esempi e, inoltre, potrai esercitarti con esercizi risolti passo dopo passo.

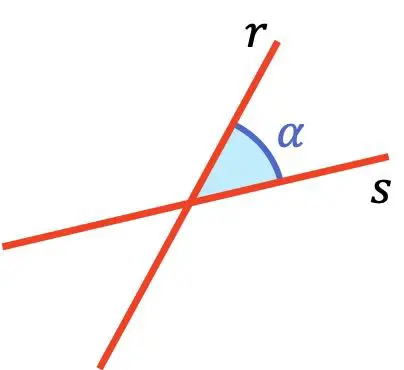
Qual è l’angolo tra due linee?

L’angolo tra due linee è l’angolo più piccolo tra queste due linee.

Nella pianta ci sono quattro tipi di linee a seconda dell’angolo che formano tra loro: linee che si intersecano (tra 0º e 90º), linee perpendicolari (90º), linee parallele (0º) e linee coincidenti (0º).

linee che si intersecano

Le linee che si intersecano si intersecano con un angolo acuto compreso tra 0º e 90º.

Rette perpendicolari

Le linee perpendicolari si intersecano ad angolo retto di 90º.

Linee parallele

Le linee parallele non si toccano mai e formano tra loro un angolo di 0º.

linee coincidenti

Due rette coincidenti hanno tutti i punti in comune e quindi tra loro esiste sempre un angolo pari a 0º.

In conclusione, il calcolo dell’angolo tra due rette parallele, coincidenti o perpendicolari è immediato: le rette parallele e le rette coincidenti formano un angolo di 0 gradi poiché hanno la stessa direzione, e le rette perpendicolari si intersecano con un angolo di 90 gradi . Per trovare invece l’angolo tra due rette che si intersecano è necessario applicare una formula (la vedremo di seguito).

Come si calcola l’angolo tra due linee?

Esistono due modi per calcolare l’angolo tra due linee. Il primo metodo utilizza il vettore direzione di ciascuna linea e il secondo metodo si basa sulla pendenza di ciascuna linea.

Nessuna procedura è migliore dell’altra, infatti entrambe sono abbastanza semplici, ma a seconda di come sono espresse le linee un metodo o un altro è pratico. Ti consigliamo quindi di sapere come utilizzare entrambi i metodi matematici.

Metodo di orientamento del vettore di linea

La formula per calcolare l’angolo tra due linee utilizzando i loro vettori di direzione è:

Dati i vettori direzione di due linee diverse:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

L’angolo tra queste due linee può essere calcolato con la seguente formula:

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

Oro

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

sono i moduli dei vettori

$\vv{\text{u}}$

$\vv{\text{v}}$

rispettivamente.

Ricorda che la formula per la grandezza di un vettore è:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

Vediamo come trovare l’angolo tra due rette con un esempio:

Calcola l’angolo tra le seguenti due linee:

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

Per calcolare l’angolo tra le due linee, devi prima trovare il vettore direzione di ciascuna linea.

la destra

$r$

è espressa sotto forma di equazione parametrica , pertanto le componenti del vettore che ne segna la direzione sono:

$\vv{r} = (-3,4)$

e la legge

$\displaystyle s$

è definito sotto forma di un’equazione implicita (o generale), quindi le coordinate del suo vettore direzione sono:

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

Ora che conosciamo il vettore direzione di ciascuna linea, possiamo usare la formula per l’angolo tra due linee:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Determiniamo quindi la grandezza dei due vettori:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

Eseguiamo le operazioni vettoriali della formula dell’angolo:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

E, infine, calcoliamo l’angolo formato dalle due rette con l’inverso del coseno:

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

Ricorda che puoi calcolare l’inverso del coseno utilizzando la calcolatrice con il tasto

$\boxed{\cos ^{-1}}.$

metodo della pendenza

Ovviamente, per comprendere questo metodo, è necessario conoscere la pendenza della retta . Puoi rivedere questo concetto nel link, dove troverai una spiegazione dettagliata di cosa significa, come si calcola, esempi ed esercizi risolti sulla pendenza di una retta.

La formula per calcolare l’angolo tra due linee dalle loro pendenze è:

Oppure due linee distinte:

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

L’angolo tra queste due linee può essere determinato con la seguente formula:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Oro

$m_1$

$m_2$

sono le pendenze delle linee

$r_1$

$r_2$

rispettivamente.

Vediamo come calcolare l’angolo tra due rette utilizzando le loro pendenze con un esempio:

Trova l’angolo tra le due linee seguenti:

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

La pendenza di ciascuna linea è il numero prima della variabile

$x:$

$m_r = 4$

$m_s = -3$

Pertanto, l’angolo tra le due linee può essere trovato applicando la formula della pendenza:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

E infine troviamo l’angolo con l’inverso della tangente:

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

Ricorda che puoi calcolare l’inverso della tangente utilizzando la calcolatrice con il tasto

$\boxed{\tan ^{-1}}.$

Abbiamo appena visto un esempio con le pendenze di due rette espresse come un’equazione esplicita, ma se fossero sotto forma di un’equazione di pendenza puntuale, si dovrebbe usare questa stessa procedura.

Risoluzione dei problemi relativi agli angoli tra due rette

Esercizio 1

Determina l’angolo formato dalle due rette seguenti:

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

vedi soluzione

In questo caso utilizzeremo il metodo del vettore di direzione. Pertanto, dobbiamo prima trovare il vettore direzione di ciascuna linea. Entrambe le linee sono espresse come equazioni parametriche, quindi le componenti dei loro vettori di direzione sono i termini che precedono il parametro

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

Ora che conosciamo il vettore direzione di ciascuna linea, possiamo usare la formula per l’angolo tra due linee:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Determiniamo quindi la grandezza dei due vettori:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

Risolviamo il prodotto scalare tra i due vettori del numeratore e la moltiplicazione dei moduli del denominatore:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

E infine troviamo l’angolo formato dalle due rette eseguendo l’inverso del coseno:

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

Esercizio 2

Trova l’angolo tra le due linee seguenti:

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

vedi soluzione

Risolveremo questo problema utilizzando il metodo del vettore di direzione, quindi prima dobbiamo trovare il vettore di direzione di ciascuna linea. la destra

$r$

è espresso sotto forma di un’equazione generale (o implicita), tale che le componenti del vettore che ne segna la direzione sono:

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

e la legge

$\displaystyle s$

è definito sotto forma di un’equazione continua, quindi le coordinate cartesiane del suo vettore direzione sono i numeri dei denominatori:

$\vv{s} = (6,3)$

Una volta conosciuto il vettore direzione di ciascuna linea, possiamo usare la formula per l’angolo tra due linee:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Determiniamo quindi i moduli dei due vettori:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

Eseguiamo le operazioni tra i vettori della formula dell’angolo:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$

E, infine, calcoliamo l’angolo formato dalle due rette con l’inverso del coseno:

$\alpha= \text{cos}^{-1}(0,98) = \bm{10,30º}$

Esercizio 3

Qual è l’angolo tra le due rette seguenti?

$\displaystyle r: \ y=-2x+9 \qquad s: \ y=5x-1$

vedi soluzione

In questo caso utilizzeremo il metodo delle pendenze delle linee per scoprire l’angolo che formano, poiché le linee hanno la forma di un’equazione esplicita.

La pendenza di ciascuna linea è il numero che accompagna la variabile indipendente

$x:$

$m_r = -2$

$m_s = 5$

Pertanto, l’angolo tra le due linee può essere determinato applicando la formula della pendenza:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-2-5}{1+5\cdot (-2)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-9} \end{vmatrix} = 0,78$

E infine troviamo l’angolo tra le due linee invertendo la tangente:

$\alpha= \text{tg}^{-1}(0,78) = \bm{37,87º}$

Esercizio 4

Trova l’equazione della retta che passa per il punto

$P(5,-1)$

e forma con la linea un angolo di 45º

$r.$

Diciamo la riga:

$\displaystyle r: \ y=2x+4$

vedi soluzione

Per risolvere il problema chiameremo

$s$

a destra che calcoleremo. Inoltre, utilizzeremo il metodo della pendenza perché conosciamo la pendenza della retta

$r:$

$m_r=2$

Dalla formula dell’angolo tra due rette (metodo della pendenza) si ottiene il valore della pendenza della retta

$s:$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

Sostituiamo i valori noti nella formula:

$\displaystyle \text{tg}(45º) =\begin{vmatrix} \cfrac{m_s-2}{1+2\cdot m_s} \end{vmatrix}$

E proviamo a risolvere l’equazione risultante:

$\displaystyle 1 =\begin{vmatrix} \cfrac{m_s-2}{1+2m_s} \end{vmatrix}$

Il valore assoluto dell’equazione la rende un po’ difficile da risolvere, perché bisogna analizzare sia le opzioni positive che quelle negative:

$\displaystyle 1 =+\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=m_s-2$

$\displaystyle 1+2m_s=m_s-2$

$\displaystyle 2m_s-m_s=-2-1$

$\displaystyle m_s=-3$

$\displaystyle 1 =-\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=-(m_s-2)$

$\displaystyle 1+2m_s=-m_s+2$

$\displaystyle 2m_s+m_s=2-1$

$\displaystyle 3m_s=1$

$\displaystyle m_s=\cfrac{1}{3}$

Abbiamo quindi due possibili soluzioni: una linea con pendenza -3 e un’altra linea con pendenza un terzo.

La formula per l’equazione punto-pendenza di una linea è:

$y-y_0=m(x-x_0)$

Pertanto, una volta conosciuta la pendenza delle due possibili rette, possiamo scrivere l’equazione punto-pendenza di ciascuna retta con il punto per il quale devono passare secondo l’enunciato,

$P(5,-1):$

$\displaystyle s: \ y+1=-3(x-5) \qquad \qquad s': \ y+1=\cfrac{1}{3}(x-5)$

Qual è l’angolo tra due linee?

Come si calcola l’angolo tra due linee?

Metodo di orientamento del vettore di linea

metodo della pendenza

Risoluzione dei problemi relativi agli angoli tra due rette

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta