Come calcolare addizione e sottrazione di matrici

In questa pagina vedremo come sommare e sottrarre matrici . Hai anche esempi che ti aiuteranno a capirlo perfettamente ed esercizi risolti in modo che tu possa esercitarti. Troverai anche tutte le proprietà dell’addizione di matrici.

Come aggiungere e sottrarre matrici?

Per calcolare un’addizione (o sottrazione) di due matrici, è necessario sommare (o sottrarre) gli elementi che occupano la stessa posizione nelle matrici.

Esempi:

esempi di addizione e sottrazione di matrici 2x2, operazioni con matrici

Nota che per sommare o sottrarre due matrici, devono avere la stessa dimensione. Ad esempio, le seguenti matrici non possono essere sommate perché la prima è una matrice 2×2 e la seconda è una matrice 3×2:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}

Esercizi risolti per addizione e sottrazione di matrici

Esercizio 1

Calcola la seguente somma di matrici 2×2:

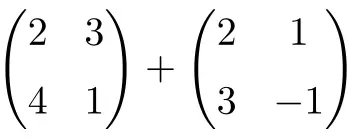
esercizio risolto passo dopo passo per l'addizione di matrici 2x2

È una somma di due matrici quadrate di dimensione 2×2:

\displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}

Esercizio 2

Esegui la seguente sottrazione di matrice:

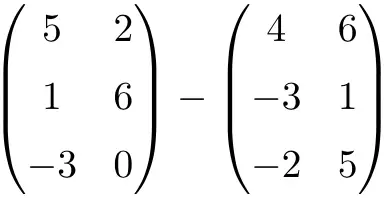
esercizio risolto passo passo sottrazione di matrici, operazioni con matrici

È una sottrazione di due matrici di dimensione 3×2:

\displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}

Esercizio 3

Trova il risultato della seguente somma di matrici di dimensione 3×3:

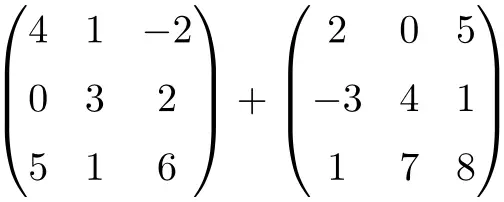
esercizio risolto passo passo di addizione di matrici 3x3, operazioni con matrici

È una somma di due matrici quadrate di ordine 3×3:

\displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}

Esercizio 4

Calcolare la seguente addizione e sottrazione di matrici quadrate di ordine 2:

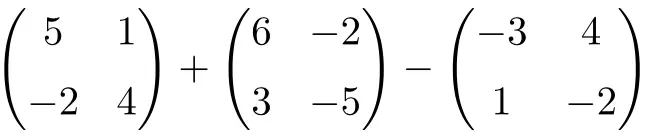
esercizio risolto passo passo addizione e sottrazione di matrici 2x2, operazioni con matrici

È un’operazione combinata con addizione e sottrazione di matrici quadrate di ordine 2:

\displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

Quindi, prima aggiungiamo le matrici a sinistra:

\displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}

E poi calcoliamo la sottrazione delle matrici:

\displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}

Esercizio 5

Risolvi le seguenti addizioni e sottrazioni di matrici:

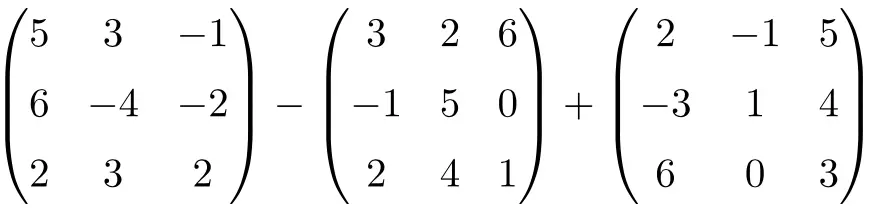
esercizio risolto passo passo addizione e sottrazione di matrici 3x3, operazioni con matrici

È un’operazione combinata di sottrazione e addizione di matrici quadrate di ordine 3:

\displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

Innanzitutto, risolviamo la sottrazione di matrice:

\displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}

E infine aggiungiamo le matrici:

\displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}

Ora che sai come sommare e sottrarre matrici, è il momento di vedere come moltiplicare le matrici , sicuramente la più importante delle operazioni sulle matrici. Troverai anche esercizi di moltiplicazione di matrici risolti passo passo per esercitarti, come in tutte le pagine di questo sito. 😉

Aggiungi proprietà della matrice

L’addizione di matrici ha le seguenti caratteristiche:

  • L’addizione di matrici ha la proprietà commutativa :

\displaystyle A +B = B + A

Pertanto, l’ordine in cui aggiungiamo le matrici è lo stesso. Per dimostrarlo, aggiungeremo due matrici cambiando il loro ordine e vedrai come il risultato è lo stesso.

Procediamo quindi ad aggiungere due matrici in un certo ordine:

\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

Notiamo che se invertiamo l’ordine di addizione delle matrici, il risultato rimane lo stesso:

\displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}

  • Un’altra proprietà dell’addizione di matrici è quella dell’elemento opposto:

\displaystyle A + (-A) =0

In altre parole, se aggiungiamo una matrice più la stessa matrice ma con tutti i suoi elementi cambiati di segno, il risultato sarà una matrice zero:

\displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}

  • L’addizione di matrici ha anche la proprietà dell’elemento neutro:

\displaystyle A + 0 =A

Questa proprietà è la più ovvia, si riferisce al fatto che qualsiasi matrice più una matrice piena di zeri equivale alla stessa matrice:

\displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}

  • L’addizione di matrici ha la proprietà associativa:

\displaystyle\left( A + B \right) + C =A + \left( B + C \right)

Pertanto, l’ordine in cui aggiungiamo le matrici è lo stesso. Guarda l’esempio seguente, dove aggiungiamo 3 matrici con ordine diverso e il risultato è lo stesso:

\displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}

\begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}

\begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto