In questo articolo troverai la spiegazione della funzione affine e della funzione lineare, nonché le differenze che esistono tra questi due tipi di funzioni. Inoltre, vedrai esempi di come rappresentare graficamente una funzione affine e una funzione lineare e come calcolare le loro espressioni da due punti. Finalmente potrai allenarti con diversi esercizi risolti passo dopo passo.
Cos’è una funzione affine e una funzione lineare?
Le definizioni di funzione affine e di funzione lineare sono le seguenti:
Una funzione affine è una funzione polinomiale di primo grado, cioè una funzione che, rappresentata sul grafico, è una retta. Le funzioni associate sono le seguenti:
![]()
Oro
![]()
è la pendenza della retta e
![]()
Questa è l’intercetta y, cioè il punto in cui la funzione interseca l’asse verticale.
In matematica, le funzioni affini sono anche chiamate trasformazioni lineari nel contesto dell’algebra lineare.
Una funzione lineare è una funzione affine che non ha un termine indipendente. Pertanto la formula per le funzioni lineari è:
![]()
Oro
![]()
è la pendenza della retta.
Il dominio e l’intervallo (o intervallo) della funzione lineare e della funzione affine sono tutti numeri reali:
![]()
![]()
Qual è la differenza tra una funzione lineare e una funzione affine?
Ora che hai visto i concetti di funzione lineare e funzione affine, avrai notato che sono molto simili tra loro. Tuttavia, la seguente differenza tra loro è molto importante:
L’unica differenza tra la funzione lineare e la funzione affine è che la funzione lineare non ha un termine indipendente mentre la funzione affine ha sempre il coefficiente dell’intercetta (n) diverso da zero (0).
Funzione lineare
![]()
funzione lineare
![]()
Ciò implica che una funzione lineare passa sempre per l’origine delle coordinate , il punto (0,0). D’altra parte, una funzione affine non passerà mai per questo punto perché ha un’intercetta diversa da 0.
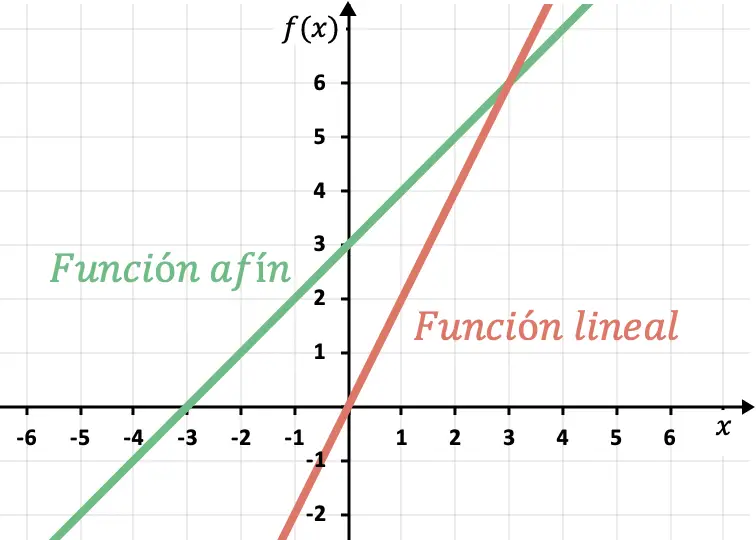
Pendenza e intercetta y di una funzione lineare o affine
In questa sezione analizzeremo un esempio di funzione affine o lineare per comprendere il significato dei termini
![]()
E
![]()
, o in altre parole, la pendenza e l’intercetta y.
- Determina l’espressione della funzione mostrata nel grafico e classificala come funzione lineare o affine.
Questi tipi di funzioni seguono la seguente espressione:
![]()
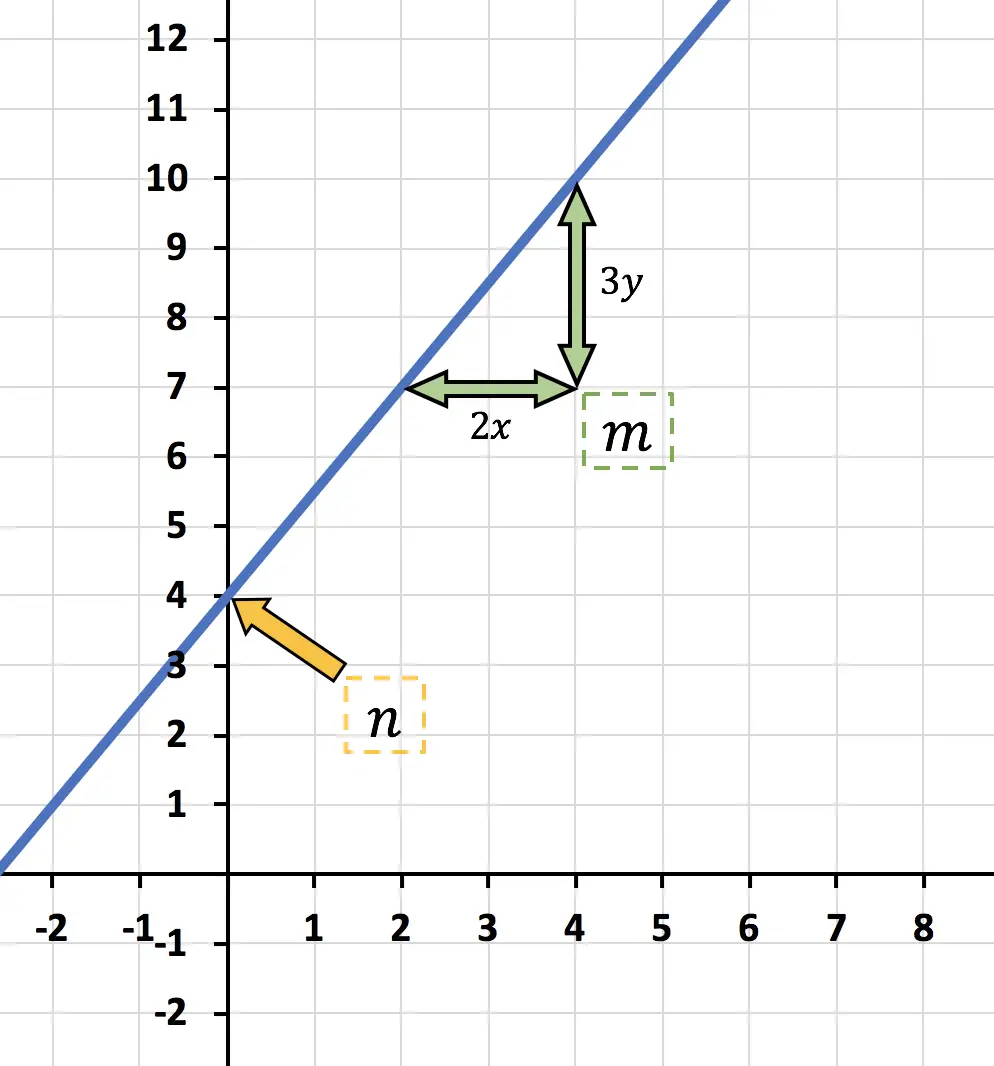
![]()
Questa è l’intercetta y, cioè il punto in cui la funzione interseca l’asse Y verticale. Quindi in questo caso:
![]()
Da un altro lato,
![]()
è la pendenza della retta. Y può essere calcolato dividendo la differenza in y tra due punti per la differenza in x tra questi stessi due punti:
![]()
![]()
dice “quanto aumenta y per ogni x” , quindi in questo caso la funzione “3y aumenta per ogni 2x” .
In conclusione, l’espressione per la funzione affine rappresentata nel grafico è:
![]()
Inoltre, poiché l’intercetta y è diversa da zero, è una funzione affine .
Di seguito ti mostriamo altri esempi di funzioni lineari e affini per completare la tua comprensione:
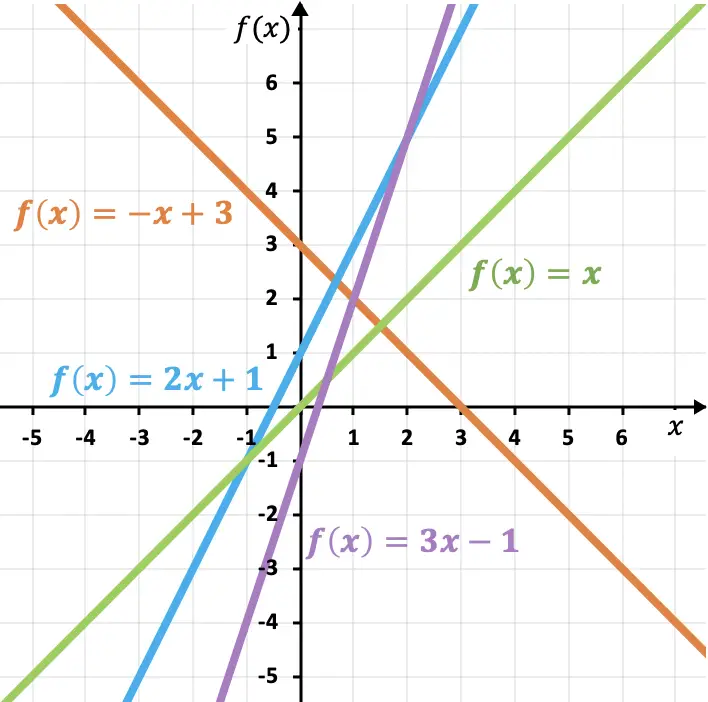
Come puoi vedere in questi esempi, maggiore è la pendenza, più ripida è la linea e, quindi, più grande è la funzione. Allo stesso modo, il coefficiente di pendenza determina la crescita o la diminuzione di una funzione:
- Se la pendenza è positiva la funzione è crescente , cioè aumenta all’aumentare di x .
- Se la pendenza è negativa la funzione è decrescente , cioè diminuisce all’aumentare di x .
Inoltre, puoi anche capire se due rette sono parallele o perpendicolari in base alle loro pendenze:
- Quando due rette hanno la stessa pendenza sono parallele , cioè non si intersecano in nessun punto oppure sono completamente identiche.
![]()
- D’altra parte, due rette sono perpendicolari , cioè si intersecano formando un angolo verticale (90º), se le loro pendenze corrispondono alla seguente relazione:
![]()
Esempio di rappresentazione di una funzione affine o lineare
Vediamo come rappresentare graficamente una funzione di primo grado utilizzando un esempio.
- Rappresentare graficamente la seguente funzione affine:
![]()
La prima cosa che dobbiamo fare è creare un array di valori. Per fare questo, garantiamo i valori che desideriamo
![]()
per ottenere valori di
![]()
:
![]()
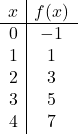
Sebbene una tabella di valori con due punti sia sufficiente, possiamo fare più punti per assicurarci che sia corretta.
Una volta creata la tabella dei valori, tracciamo i punti sul grafico:
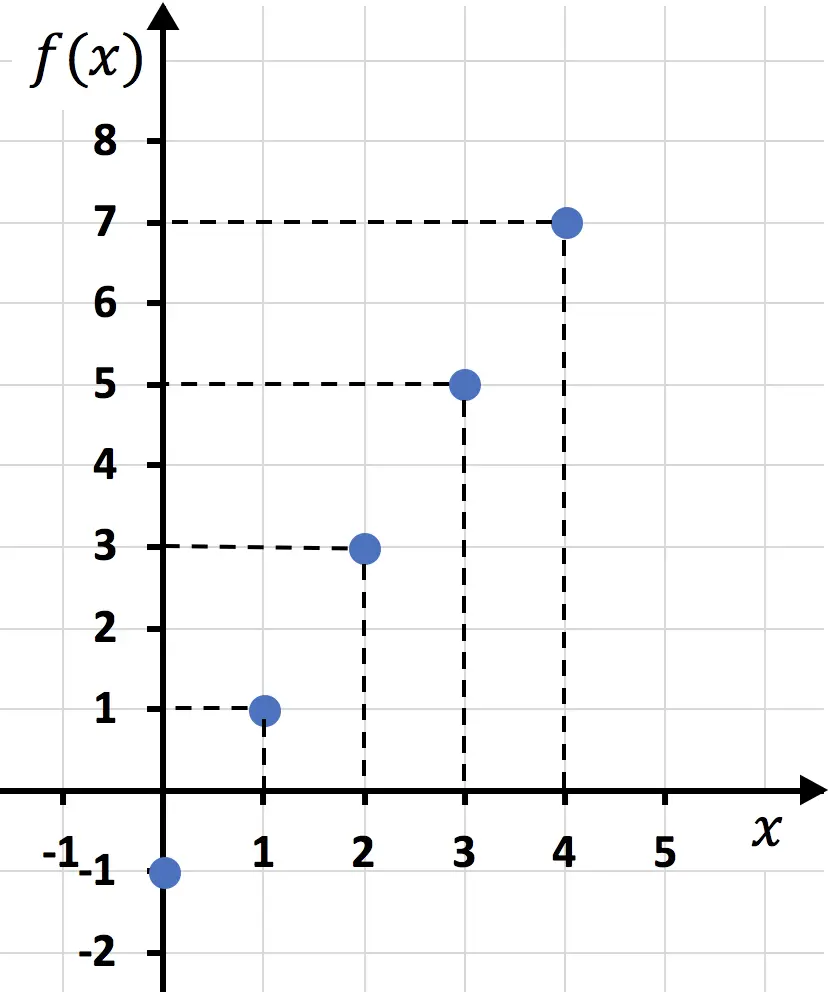
E infine, uniamo i punti e tracciamo una linea:
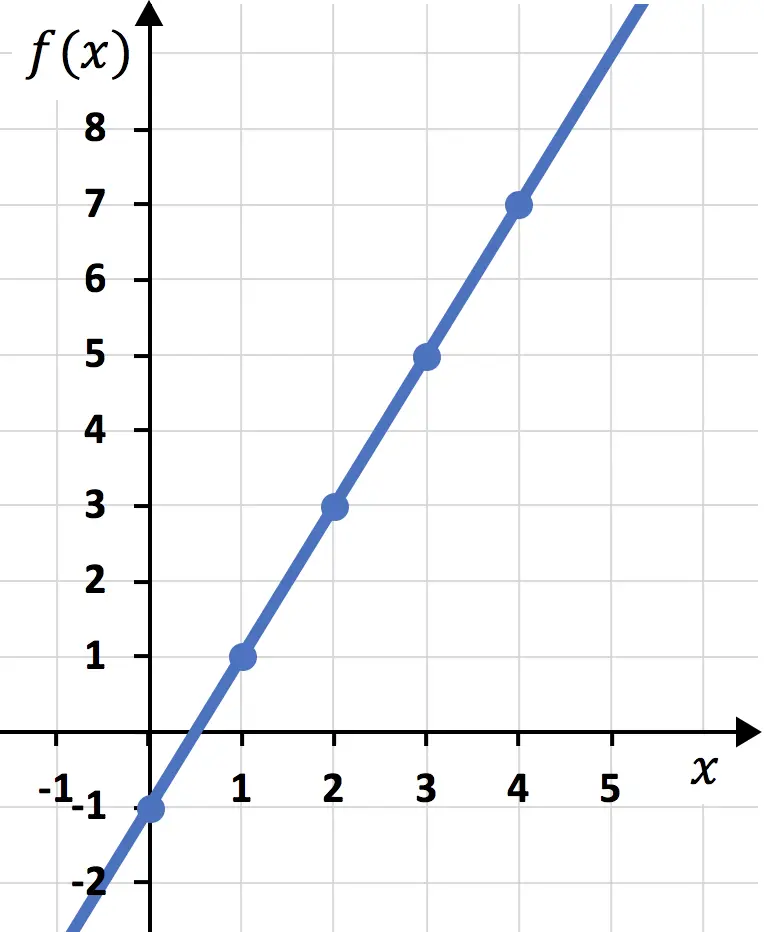
E in questo modo abbiamo già rappresentato la funzione su un grafico. Come puoi vedere, non è complicato, devi solo creare prima una tabella di valori e poi tracciare i punti su un grafico.
Come calcolare una funzione lineare o affine da due punti
Vediamo ora come trovare una funzione lineare o affine da due punti utilizzando un esempio:
- Calcolare la funzione lineare che soddisfa
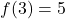
e andare oltre il punto
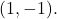
Prima di tutto,
![]()
Ciò significa che la funzione passa per il punto
![]()
.
Pertanto, poiché abbiamo due punti attraverso i quali passa la funzione, possiamo calcolare la pendenza
![]()
funzione:
Considerando due punti,
![]()
E
![]()
, pendenza
![]()
della funzione si calcola:
![]()
Nel nostro caso la funzione passa per i punti
![]()
E
![]()
. Quindi la pendenza
![]()
della funzione è:
![]()
La funzione sarà quindi della forma:
![]()
Una volta che lo sappiamo
![]()
possiamo risolvere il mistero
![]()
. Per fare ciò, sostituiamo nell’equazione le coordinate di un punto appartenente alla funzione. Ad esempio il punto (3.5):
![]()
Risolviamo l’equazione risultante:
![]()
![]()
![]()
![]()
La funzione lineare è quindi:
![]()
Esercizi risolti su funzioni lineari e affini
Esercizio 1
Determinare la pendenza e l’origine della seguente funzione affine:
![]()
Una funzione lineare ha la forma
![]()
La pendenza della funzione è quindi il numero che accompagna x , che in questo caso è -5:
![]()
E l’intercetta y è il termine indipendente, che in questo caso è -2:
![]()
Esercizio 2
Rappresentare graficamente la seguente funzione affine:
![]()
Per prima cosa diamo valori a
![]()
per creare la tabella dei valori:
![]()
![]()
![]()
![]()
![]()
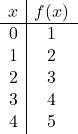
E poi rappresentiamo i punti della tabella dei valori sul grafico e tracciamo la linea:

Esercizio 3
Traccia la seguente funzione affine sul grafico:
![]()
Per prima cosa diamo valori a
![]()
per creare la tabella dei valori:
![]()
![]()
![]()
![]()
![]()
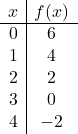
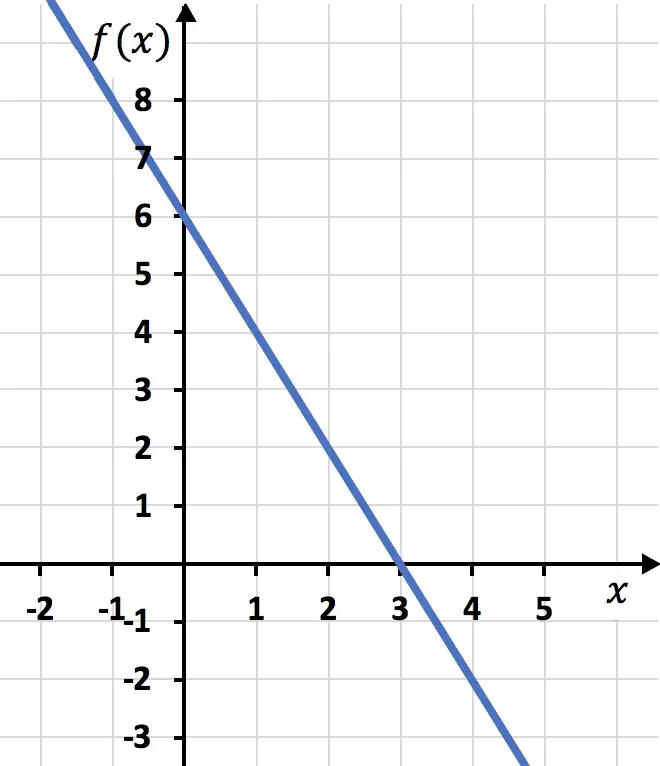
E infine rappresentiamo i punti della tabella dei valori sul grafico e tracciamo la linea:
Esercizio 4
Trova l’espressione della funzione affine che passa per i punti (2,3) e (0,1).
La funzione passa per i punti (2,3) e (0,1), quindi la pendenza della funzione è:
![]()
E la funzione sarà della forma:
![]()
Una volta conosciuto m, possiamo calcolare n . Per fare ciò, dobbiamo sostituire nell’equazione le coordinate di un punto appartenente alla funzione. Ad esempio il punto (2,3):
![]()
![]()
Dobbiamo ora risolvere l’equazione risultante:
![]()
![]()
La funzione corrisponde quindi alla seguente espressione:
![]()
Esercizio 5
Rappresentare graficamente la seguente funzione affine:
![]()
Per prima cosa diamo valori a
![]()
per creare la tabella dei valori:
![]()
![]()
![]()
![]()
![]()

E poi rappresentiamo i punti della tabella dei valori sul grafico e tracciamo la linea:

Esercizio 6
Calcolare la funzione lineare che soddisfa le seguenti due condizioni:
![Rendered by QuickLaTeX.com \begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3d1692f49f622f3167c7b58da6553eb_l3.png)
Possa realizzarsi
![]()
Ciò significa che la funzione passa per il punto (3,-2). E, allo stesso modo,
![]()
Ciò significa che la funzione passa per il punto (-1.6).
Quindi la funzione passa per i punti (3,-2) e (-1,6), quindi la sua pendenza è:
![]()
La funzione sarà quindi della forma:
![]()
E una volta conosciuto m, possiamo calcolare n . Per fare ciò, sostituiamo nell’equazione le coordinate di un punto che appartiene alla funzione. Ad esempio il punto (3,-2):
![]()
E risolviamo l’equazione risultante:
![]()
![]()
![]()
La funzione è quindi:
![]()
Esercizio 7
Trova la funzione affine che svolge
![]()
e passa per il punto (3.5).
Possa realizzarsi
![]()
Ciò significa che la funzione passa per il punto (1,6).
La funzione passa quindi per i punti (1.6) e (3.5) e quindi la sua pendenza è:
![]()
La funzione sarà quindi della forma:
![]()
Una volta conosciuto il termine m possiamo calcolare il coefficiente n . Per fare ciò, sostituiamo nell’equazione le coordinate di un punto che appartiene alla funzione. Ad esempio il punto (1,6):
![]()
Risolviamo l’equazione risultante:
![]()
![]()
Ricorda che per sommare le frazioni, devi prima ridurle a un denominatore comune e poi sommare i numeratori:
![]()
![]()
![]()
La funzione è quindi:
![]()
Esercizio 8
Risolvi il seguente problema relativo alle funzioni lineari e affini:
Un negozio vende 40 unità di un prodotto quando il prezzo è 15 €/unità e 65 unità quando il prezzo è 10 €/unità.
- Calcolare la funzione di domanda del prodotto, supponendo che sia una funzione affine.
- Quante unità verranno vendute se il prezzo è fissato a 12 €/unità?
Poiché si tratta di una funzione affine, la funzione sarà del tipo
![]()
Oro
![]()
sarà il prezzo unitario del prodotto e
![]()
saranno le unità vendute.
Il comunicato stampa ci dice che quando il prezzo è di 15€/unità, vengono vendute 40 unità. Pertanto, come
![]()
è il prezzo e
![]()
unità vendute, deve essere rispettata la seguente uguaglianza:
![]()
E quando il prezzo è di 10€/unità, vengono vendute 65 unità. Quindi, utilizzando lo stesso ragionamento:
![]()
Possa realizzarsi
![]()
Ciò significa che la funzione passa per il punto (15.40). E
![]()
Ciò significa che la funzione passa per il punto (10.65).
La pendenza della funzione è quindi:
![]()
La funzione sarà quindi della forma:
![]()
Una volta conosciuto m, possiamo calcolare n . Per fare ciò, sostituiamo nell’equazione le coordinate di un punto che appartiene alla funzione. Ad esempio il punto (15:40):
![]()
E risolviamo l’equazione risultante:
![]()
![]()
![]()
La funzione che lega le vendite effettuate al prezzo è quindi:
![]()
D’altra parte, nella funzione
![]()
rappresenta il prezzo. Pertanto, per sapere quante unità verranno vendute se il prezzo è di 12 €/unità, dobbiamo fare un calcolo
![]()
![]()
![]()
![]()
Quindi se il prezzo è 12€/unità , verranno vendute 55 unità.