In questo articolo spieghiamo come derivare l’arcotangente iperbolica di una funzione. Inoltre, potrai vedere esempi risolti della derivata dell’arcotangente iperbolica.
Formula per la derivata dell’arcotangente iperbolica
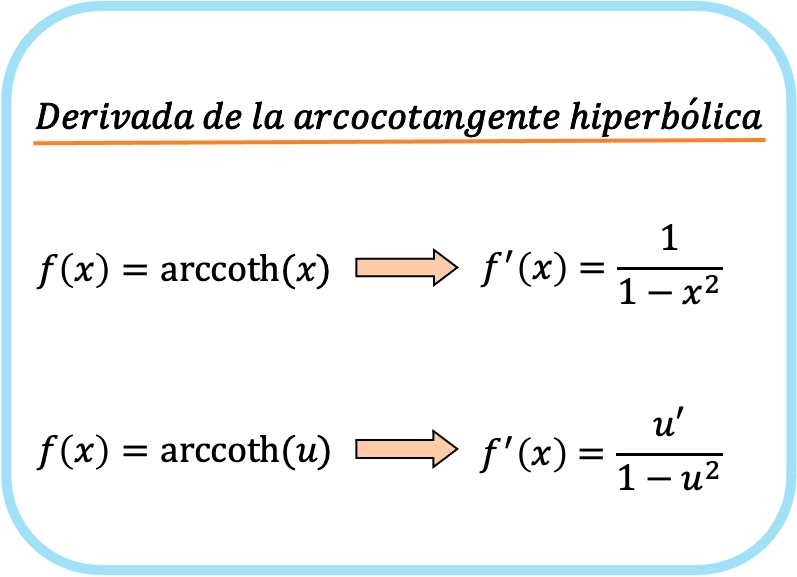
La derivata dell’arcotangente iperbolica di x è uno su uno meno x al quadrato.
![]()
Pertanto, la derivata dell’arcotangente iperbolica di una funzione è uguale al quoziente della derivata di quella funzione diviso per uno meno quella funzione al quadrato.
![]()
Nota che la seconda formula è come la prima ma applica la regola della catena, quindi potrebbero effettivamente essere considerate la stessa formula.
In alcuni libri di matematica potresti vedere che la derivata di questo tipo di funzione trigonometrica inversa è:
![]()
Tuttavia, se guardi attentamente, sono la stessa formula, l’unica differenza è che il numeratore e il denominatore della frazione sono stati moltiplicati per -1.
Esempi di derivata dell’arcotangente iperbolica
Esempio 1
![]()
Nell’argomento dell’arcotangente iperbolico abbiamo una funzione diversa da x, quindi dobbiamo usare la formula della regola della catena per derivarla:
![]()
La derivata di 5x è 5, quindi metti 5 al numeratore della frazione e metti meno 5x al quadrato al denominatore:
![]()
Esempio 2
![]()
Per risolvere la derivata di questa funzione, dobbiamo applicare la formula per la derivata dell’arcotangente iperbolica, che è la seguente:
![]()
In questo caso abbiamo una funzione composta, poiché nell’argomento della funzione trigonometrica è presente una funzione esponenziale. Quindi dobbiamo usare la regola della catena per trovare la derivata dell’intera funzione:
![]()