Qui spieghiamo come derivare la cotangente iperbolica di una funzione. Troverai anche esempi di derivata della cotangente iperbolica.
Formula per la derivata della cotangente iperbolica
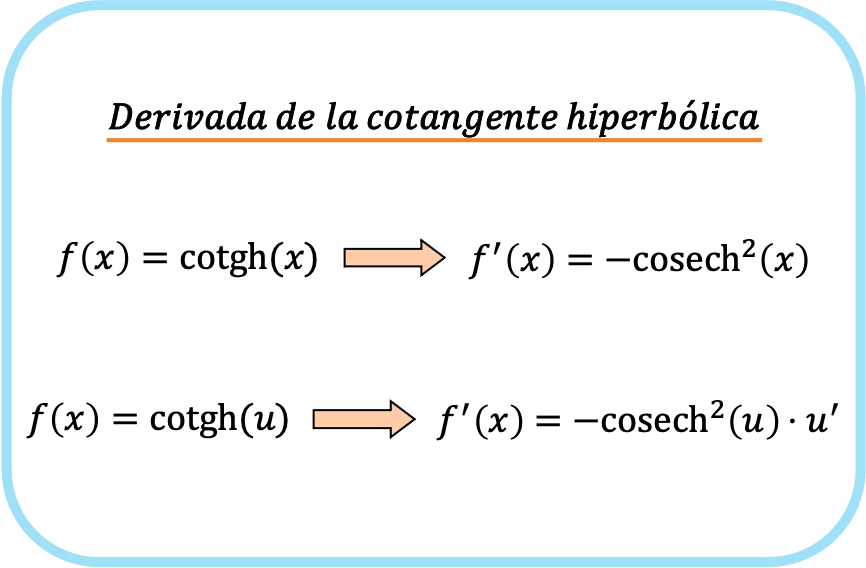
La derivata della cotangente iperbolica di x è uguale a meno la cosecante iperbolica di x al quadrato.
![]()
Pertanto, la derivata della cotangente iperbolica di una funzione è meno la cosecante iperbolica della funzione moltiplicata per la derivata di quella funzione.
![]()
Tieni presente che nella seconda formula è stata applicata la regola della catena e questa formula viene utilizzata quando è presente una funzione diversa da x nell’argomento della cotangente iperbolica.
In alcuni libri di matematica potresti trovare che la derivata della cotangente è un’altra, poiché le tre espressioni seguenti sono equivalenti:
![]()
Ovviamente puoi usare l’espressione che preferisci tra le tre per ricavare la cotangente iperbolica, ma la più usata è la cosecante iperbolica al quadrato.
Esempi di derivata della cotangente iperbolica
Una volta che sappiamo qual è la formula per la derivata della cotangente iperbolica di una funzione, risolveremo diversi esempi di questo tipo di derivate trigonometriche.
Esempio 1
In questo esempio vedremo qual è la derivata della cotangente iperbolica della funzione 2x.
![]()
Nell’argomento della cotangente iperbolica abbiamo una funzione diversa da x, quindi dobbiamo usare la formula con la regola della catena per fare la derivazione:
![]()
Poiché 2x è un termine di primo grado, la sua derivata è 2. Quindi, per trovare la derivata della cotangente iperbolica di 2x, inseriamo semplicemente 2x nell’argomento al quadrato della cosecante iperbolica e moltiplichiamo per 2.
![]()
Esempio 2
Nel secondo esempio determineremo il valore della derivata della cotangente iperbolica di una funzione polinomiale.
![]()
Come abbiamo visto sopra, la regola per derivare la cotangente iperbolica di una funzione è la seguente:
![]()
Pertanto la derivata della cotangente iperbolica di questo esercizio sarà la seguente:
![]()