Qui troverai la formula per la derivata dell’arcotangente e spiegheremo come derivare l’arcotangente di una funzione con esempi.
formula della derivata arcotangente
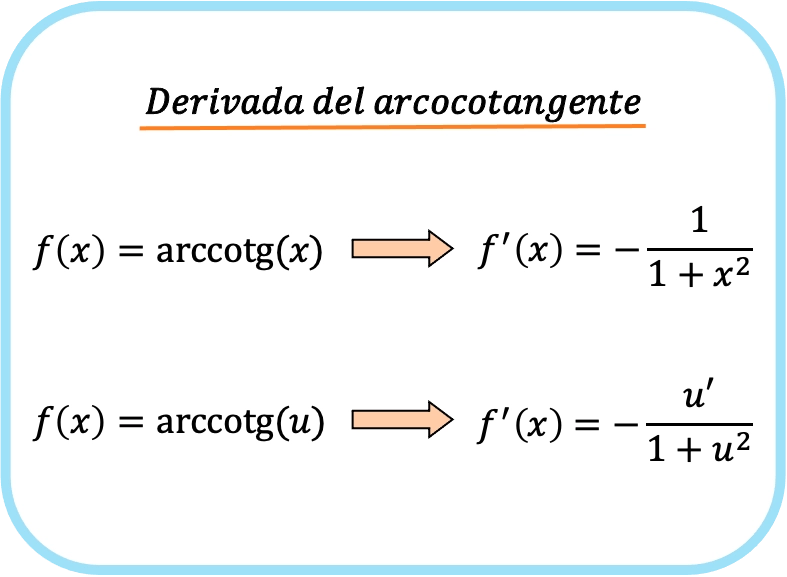
La derivata dell’arcotangente di x è negativa uno diviso uno più x al quadrato.
![]()
Pertanto, la derivata dell’arcotangente di una funzione è uguale a meno la derivata di quella funzione divisa per uno più la funzione al quadrato.
![]()
Tieni presente che la prima e la seconda formula sono identiche, l’unica differenza è che la regola della catena viene applicata alla seconda espressione. Infatti, se sostituisci u con una x, otterrai la prima formula poiché la derivata della funzione x è 1.
Sebbene l’arcotangente sia la funzione inversa della cotangente, le loro derivate sono abbastanza diverse. Infatti la cotangente di una funzione ha tre modi per essere derivata, puoi vederli tutti qui:
➤ Vedi: formula per la derivata della cotangente
Esempi di derivata dell’arcotangente
Dopo aver visto qual è la formula per la derivata dell’arcotangente, ecco due esercizi risolti di questo tipo di derivata trigonometrica. Ricorda inoltre che se hai qualche domanda puoi lasciare la tua domanda qui sotto nei commenti.
Esempio 1
In questo esempio vedremo quanto vale la derivata dell’arcotangente della funzione quadratica x 2 .
![]()
Nell’argomento dell’arcotangente abbiamo una funzione diversa da x, quindi dobbiamo applicare la formula per la derivata dell’arcotangente con la regola della catena:
![]()
La derivata di x elevata a due è 2x, quindi al numeratore dobbiamo mettere 2x e al denominatore la funzione dell’argomento al quadrato:
![]()
Esempio 2
In questo secondo esempio deriveremo l’arcotangente di una funzione polinomiale di terzo grado.
![]()
Usiamo la regola della derivata dell’arcotangente per eseguire la sua derivazione:
![]()
Quindi la derivata dell’arcotangente della funzione è:
![]()