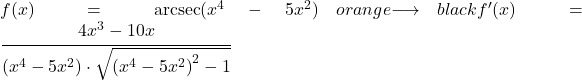In questa pagina vedrai qual è la derivata dell’arcosecante (formula). Troverai esercizi risolti per le derivate dell’arcosecante di una funzione.
Formula della derivata arcsecante
La derivata dell’arcosecante di x è uno fratto il prodotto di x per la radice di x al quadrato meno 1.
![]()
Pertanto, la derivata dell’arcosecante di una funzione è uguale al quoziente della derivata di quella funzione diviso per la funzione moltiplicata per la radice di quella funzione al quadrato meno uno.
![]()
Ovviamente la seconda formula è simile alla prima formula, l’unica differenza tra le due è che nella seconda formula viene applicata la regola della catena.

Anche se può sembrare strano trattandosi di funzioni inverse, la derivata dell’arcosecante non ha nulla a che vedere con la derivata della secante. Puoi vedere la formula per la derivata della secante cliccando qui:
➤ Vedi: derivata della secante
Esempi di derivata arcosecante
Esempio 1
In questo esempio vedremo quanto vale la derivata dell’arcosecante della funzione lineare 7x.
![]()
Per trovare la derivata dell’arcosecante è necessario applicare la formula corrispondente, che è la seguente:
![]()
La derivata della funzione 7x è 7, quindi la derivata dell’arcosecante della funzione 7x è:
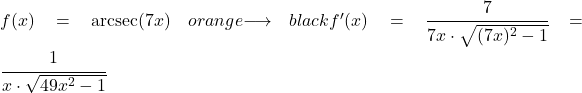
Esempio 2
In questo secondo esempio, deriveremo l’arcosecante di una funzione potenziale.
![]()
Poiché nell’argomento della funzione arcosecante è presente un termine diverso da x, è necessario applicare la regola della derivata arcosecante con la regola della catena per derivare l’intera funzione.
![]()
Quindi, al numeratore scriviamo la derivata dell’argomento della funzione, e al denominatore riscriviamo la funzione potenziale e la moltiplichiamo per la radice quadrata della funzione dell’argomento elevata alla potenza di 2 meno 1: