Derivato dell'arcoseno iperbolico

Qui troverai qual è la derivata dell’arcoseno iperbolico (formula). Inoltre, potrai vedere diversi esercizi risolti sulle derivate dell’arcoseno iperbolico di una funzione. Infine, ti mostriamo la formula per la derivata di questo tipo di funzione trigonometrica.

Formula del derivato dell’arcoseno iperbolico

La derivata dell’arcoseno iperbolico di x è uno fratto la radice quadrata di x al quadrato più 1.

f(x)=\text{arcsenh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2+1}}

Quindi la derivata dell’arcoseno iperbolico di una funzione è uguale al quoziente della derivata di quella funzione diviso per la radice quadrata di quella funzione al quadrato più uno.

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

La seconda formula è come la prima ma applica la regola della catena. Cioè, con la prima formula si può ricavare solo l’arcoseno iperbolico di xy, mentre con la seconda formula si può ricavare l’arcoseno iperbolico di qualsiasi funzione.

derivato dall'arcoseno iperbolico

Tieni presente che l’arcoseno iperbolico è la funzione inversa del seno iperbolico, la cui derivata puoi vedere qui:

➤ Vedi: formula per la derivata del seno iperbolico

Esempi di derivata dell’arcoseno iperbolico

Esempio 1

f(x)=\text{arcsenh}(3x)

Per risolvere la derivata della funzione arcoseno utilizziamo la formula vista sopra:

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

La derivata di 3x è 3, quindi 3 va al numeratore. E al denominatore dobbiamo semplicemente mettere la radice quadrata di 3x al quadrato più 1:

f(x)=\text{arcsenh}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{\sqrt{(3x)^2+1}}=\cfrac{3}{\sqrt{9x^2+1}}

Esempio 2

f(x)=\text{arcsenh}(x^3)

Per ricavare l’arcoseno iperbolico della funzione x al cubo dobbiamo applicare la stessa formula:

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

La derivata di x al cubo è 3x 2 , quindi la derivata dell’arcoseno iperbolico di x elevato a 3 sarà:

f(x)=\text{arcsenh}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3x^2}{\sqrt{\left(x^3\right)^2+1}}=\cfrac{3x^2}{\sqrt{x^6+1}}

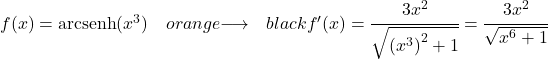
Dimostrazione della derivata dell’arcoseno iperbolico

Dimostreremo la formula per la derivata dell’arcoseno iperbolico:

y=\text{arcsenh}(x)

Per prima cosa trasformiamo l’arcoseno iperbolico in un seno iperbolico:

x=\text{senh}(y)

Deduciamo da entrambi i lati dell’uguaglianza:

1=\text{cosh}(y)\cdot y'

Ti chiariamo:

y'=\cfrac{1}{\text{cosh}(y)}

Quindi applichiamo l’identità trigonometrica che collega il seno iperbolico e il coseno iperbolico:

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{cosh}(y)=\sqrt{1+\text{senh}^2(y)}

y'=\cfrac{1}{\sqrt{1+\text{senh}^2(y)}}

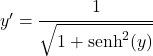
Ma sopra abbiamo dedotto che x corrisponde al seno iperbolico di y, quindi l’equazione rimane:

y'=\cfrac{1}{\sqrt{1+x^2}}

Come puoi vedere, applicando questi passaggi abbiamo ottenuto la formula per la derivata dell’arcoseno iperbolico, motivo per cui è stata dimostrata.

Articoli simili

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto