Qui troverai qual è la derivata della tangente iperbolica di una funzione. Inoltre, potrai vedere diversi esempi risolti di derivate di tangenti iperboliche. E infine, ti mostriamo la formula per la derivata della tangente iperbolica.
Formula per la derivata della tangente iperbolica
La derivata della tangente iperbolica di x è uguale a 1 diviso per il quadrato del coseno iperbolico di x. Anche la derivata della tangente di x è equivalente al quadrato della secante iperbolica di x e 1 meno il quadrato della tangente iperbolica di x.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a7c392afdb3bbf504e167e15fb2fee6_l3.png)
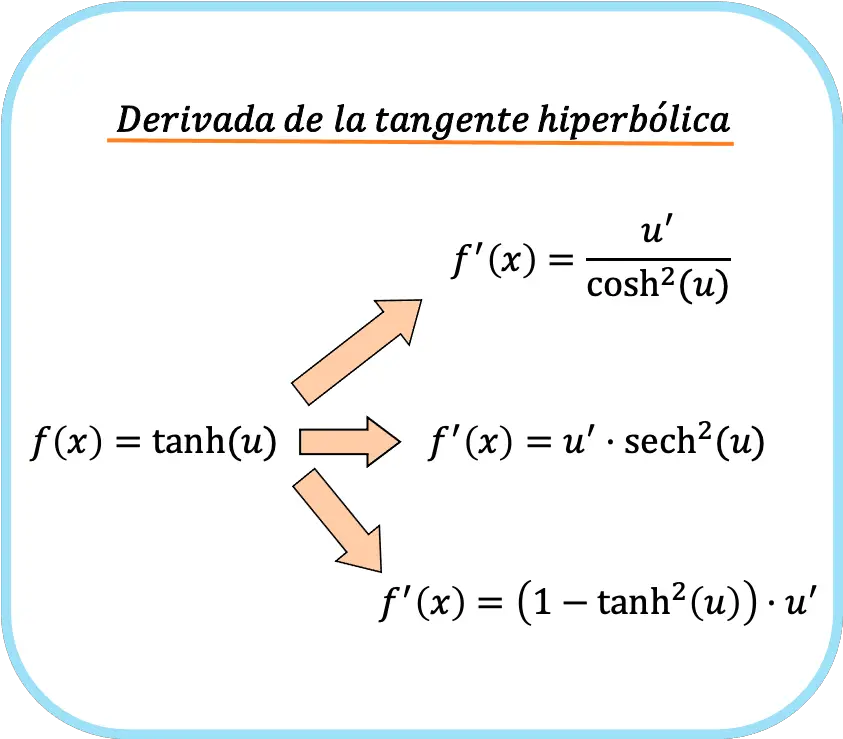
Se invece nell’argomento funzione abbiamo una funzione diversa da x, dobbiamo applicare la regola della catena. E poi le tre formule per la derivata della tangente iperbolica sono:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5ee01c6675067b20f71ea8ac4efcfe5_l3.png)
Ciò non significa che ogni volta che ricaviamo la tangente iperbolica dobbiamo usare tutte e tre le formule, ma piuttosto che possiamo usarne una qualsiasi per ricavarla. Quindi, a seconda della funzione dell’argomento tangente iperbolica, sarà meglio utilizzare una formula o un’altra. Di seguito sono riportati alcuni esempi in cui è possibile vedere come viene derivata la tangente iperbolica di una funzione.
La derivata della tangente iperbolica è quasi identica alla derivata della tangente, ma ha un piccolo dettaglio che le rende totalmente diverse. Puoi vedere qual è la differenza nel seguente link:
➤ Vedi: formula della derivata tangente
Esempi di derivata della tangente iperbolica
Dopo aver visto qual è la formula per la derivata della tangente iperbolica, ecco alcuni esempi risolti di derivate di questo tipo di funzioni trigonometriche in modo da comprendere appieno come derivare la tangente iperbolica.
Esempio 1: Derivata della tangente iperbolica di 2x
![]()
Per ricavare la tangente iperbolica in questo esempio, utilizzeremo la formula del coseno iperbolico, anche se ovviamente puoi usare quella che preferisci.
![]()
Sappiamo che la derivata di 2x è 2, quindi la derivata dell’intera funzione è:
![]()
Esempio 2: Derivata della tangente iperbolica di x al quadrato
![]()
La regola per la derivata della tangente iperbolica di una funzione è:
![]()
Da un lato differenziamo la funzione dall’argomento x 2 , che dà 2x, e poi risolviamo la derivata dell’intera funzione utilizzando la formula:
![]()
Esempio 3: Derivata della tangente iperbolica al cubo
![]()
In questo caso dobbiamo ricavare la tangente iperbolica di una funzione che, peraltro, è elevata a potenza. Dobbiamo quindi utilizzare la formula per la derivata di una funzione potenziale, la regola per la derivata della tangente iperbolica e la regola della catena:
![]()
Dimostrazione della derivata della tangente
In questa sezione dimostreremo la formula per la derivata della tangente iperbolica. E, per questo, partiremo dall’identità trigonometrica che collega i tre rapporti trigonometrici iperbolici:
![]()
➤ Nota: per comprendere la dimostrazione, è necessario sapere qual è la derivata del seno iperbolico e qual è la derivata del coseno iperbolico . Ti consigliamo pertanto di visitare le pagine collegate prima di proseguire.
Ora applichiamo la formula per la derivata di un quoziente:
![]()
![]()
![]()
Riduciamo l’espressione del numeratore della frazione utilizzando la seguente formula:
![]()
![]()
Come puoi vedere, l’uguaglianza precedente corrisponde alla prima formula per la derivata della tangente iperbolica. Allo stesso modo, la secante iperbolica è l’inverso moltiplicativo del coseno iperbolico, quindi si deriva anche la seconda formula:
![]()
Infine, possiamo arrivare alla terza regola della derivata della tangente iperbolica convertendo la frazione del passaggio precedente in una sottrazione di frazioni:
![]()
![]()
![]()