Derivato di una funzione lineare

In questo articolo ti mostriamo quanto vale la derivata di una funzione lineare. Inoltre, risolviamo diversi esempi di derivate di funzioni lineari e dimostriamo la formula per questo tipo di derivata. Troverai anche esercizi risolti sulle derivate delle funzioni lineari.

Qual è la derivata di una funzione lineare?

La derivata di una funzione lineare è il coefficiente del termine di primo grado , vale a dire che la derivata di una funzione lineare f(x)=Ax+B è uguale ad A.

$f(x)=Ax+B\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=A$

Il termine indipendente viene rimosso dalla derivata perché la derivata di una costante è zero. E d’altra parte la derivata di un termine di primo grado è il coefficiente di detto termine. Pertanto, la derivata della somma di questi due tipi di funzioni è il coefficiente del termine lineare.

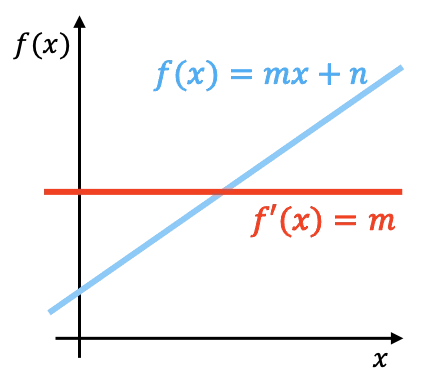
Dal punto di vista geometrico, la derivata di una funzione lineare è la pendenza di quella funzione. Nel grafico qui sopra puoi vedere rappresentata una funzione lineare con la sua derivata.

Esempi di derivate di funzioni lineari

Data la definizione di derivata di una funzione lineare, calcoleremo alcuni esempi di funzioni lineari per completare la comprensione del concetto:

$\begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}$

Tieni presente che la derivata della funzione lineare è sempre il numero che accompagna la variabile x quando la funzione non ha un termine indipendente, o in altre parole, se ha un solo termine di primo grado. Per esempio:

$f(x)=8x\quad\longrightarrow\quad f'(x)=8$

Pertanto, la derivata di una funzione lineare è una funzione senza variabile indipendente, un numero semplice.

Dimostrazione della derivata di una funzione lineare

Successivamente, dimostreremo la formula per la derivata di una funzione lineare.

Sia f una funzione lineare qualsiasi:

$f(x)=Ax+B$

La formula per calcolare la derivata di una funzione in un punto è:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$

Quindi, se calcoliamo il limite precedente per una funzione lineare, otteniamo:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}=\frac{A(a+h)+B-(A\cdot a+B)}{h}$

Risolviamo le parentesi:

$\displaystyle f'(a)=\frac{Aa+Ah+B-Aa-B}{h}$

Operiamo al numeratore:

$\displaystyle f'(a)=\frac{Ah}{h}$

Infine semplifichiamo la frazione:

$\displaystyle f'(a)=A$

In conclusione, la derivata di una funzione lineare è uguale in ogni punto al coefficiente del termine di primo grado. Pertanto, viene derivata la formula per la derivata di una funzione lineare.

Risolti problemi di derivate di funzioni lineari

Calcolare le derivate delle seguenti funzioni lineari:

$\text{A)}\ f(x)=2x-25$

$\text{B)}\ f(x)=x+3$

$\text{C)}\ f(x)=-9x-1$

$\text{D)}\ f(x)=\cfrac{1}{2}x+7$

$\text{E)}\ f(x)=5x$

$\text{F)}\ f(x)=\sqrt{7}x+\frac{3}{4}$

vedi soluzione

Per derivare una funzione lineare è sufficiente eliminare il termine costante e la variabile dalla funzione, in modo che rimanga solo il coefficiente del termine lineare. Ancora:

$\text{A)}\ f'(x)=2$