Questa pagina spiega cosa sono le funzioni di proporzionalità inversa e come rappresentarle graficamente. Inoltre troverai tutte le caratteristiche di questo tipo di funzioni, come calcolarne il dominio e anche diversi esempi ed esercizi risolti passo passo per esercitarti.
Cos’è una funzione di proporzionalità inversa?
Una funzione di proporzionalità inversa è una funzione che mette in relazione due quantità inversamente proporzionali, vale a dire che una quantità aumenta quando l’altra diminuisce e viceversa. In generale, le funzioni di proporzionalità inversa sono definite dalla seguente formula:
![]()
Oro
![]()
è una costante chiamata rapporto di proporzionalità.
Pertanto, le funzioni di proporzionalità inversa sono sempre composte da frazioni con un polinomio di primo grado al denominatore. Pertanto, sono un tipo di funzione razionale.
Esempi di funzioni di proporzionalità inversa:
![]()
Generalmente
![]()
è generalmente la variabile indipendente e
![]()
la variabile dipendente, o in altre parole, la variabile
![]()
dipende da
![]()
D’altra parte, il rapporto di proporzionalità (il termine numeratore) può essere positivo o negativo e il suo segno segna l’aumento o la diminuzione della funzione:
- Se la costante

è negativo, la funzione è crescente.
- Se invece la costante

è positivo, la funzione è decrescente.
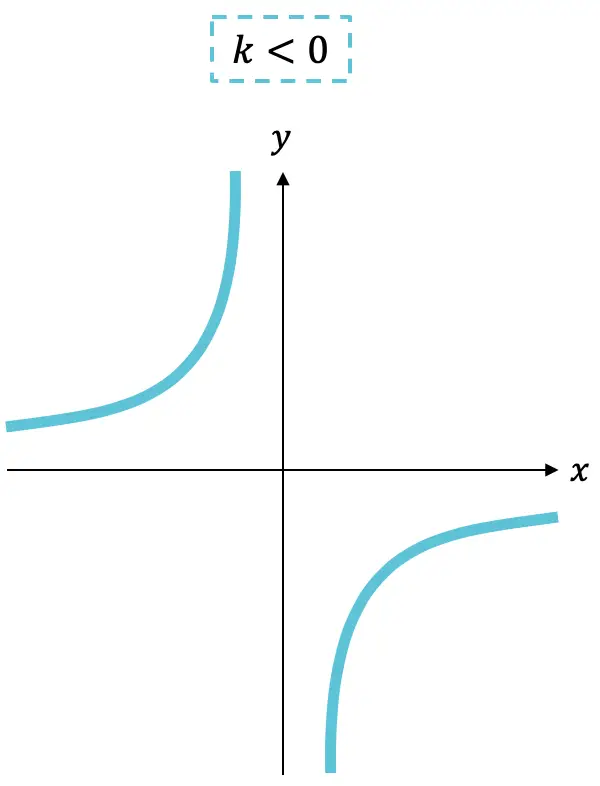
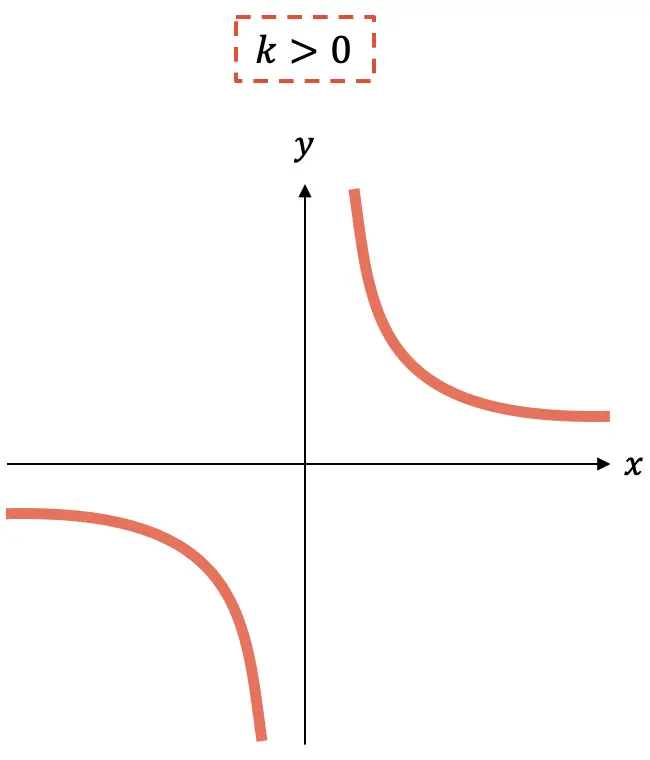
Come puoi vedere, il grafico di una funzione di proporzionalità inversa è sempre composto da due iperboli che, a seconda del segno di k , si troveranno in un quadrante o nell’altro.
Dominio di una funzione di proporzionalità inversa
Essendo un tipo di funzione razionale, il dominio di una funzione di proporzionalità inversa è costituito da tutti i numeri reali tranne quelli che scompaiono dal denominatore . Perché il denominatore non può mai essere zero perché ciò risulterebbe nell’infinito.
Ad esempio, determineremo il dominio della seguente funzione di proporzionalità inversa:
![]()
Per sapere quando il denominatore è zero, dobbiamo uguagliare la sua espressione a 0 e risolvere l’equazione:
![]()
![]()
Quindi, quando x assume il valore 1, il denominatore sarà zero e otterremo l’indeterminazione. Quindi il dominio della funzione è composto da tutti i numeri reali meno
![]()
![]()
Come rappresentare graficamente una funzione di proporzionalità inversa
Vedremo come rappresentare graficamente una funzione di proporzionalità inversa utilizzando un esempio.
- Rappresenteremo in un grafico la seguente funzione:
![]()
La prima cosa che dobbiamo fare è trovare il dominio della funzione. Essendo una frazione, il denominatore non può mai essere 0, perché ciò darebbe come risultato l’infinito. Pertanto il dominio sarà tutto x tranne quando si annulla il denominatore.
Poniamo quindi il denominatore uguale a 0 per vedere quale x non appartiene al dominio:
![]()
![]()
Pertanto, il dominio della funzione è composto da tutti i numeri tranne 2:
![]()
Una volta che sappiamo quale numero non appartiene al dominio, creiamo una tabella di valori. Per rappresentare funzioni di proporzionalità inversa è necessario calcolare 3 o 4 punti a sinistra e 3 o 4 punti a destra del numero che non appartiene al dominio (2):
![]()

Rappresentiamo ora i punti su un grafico :
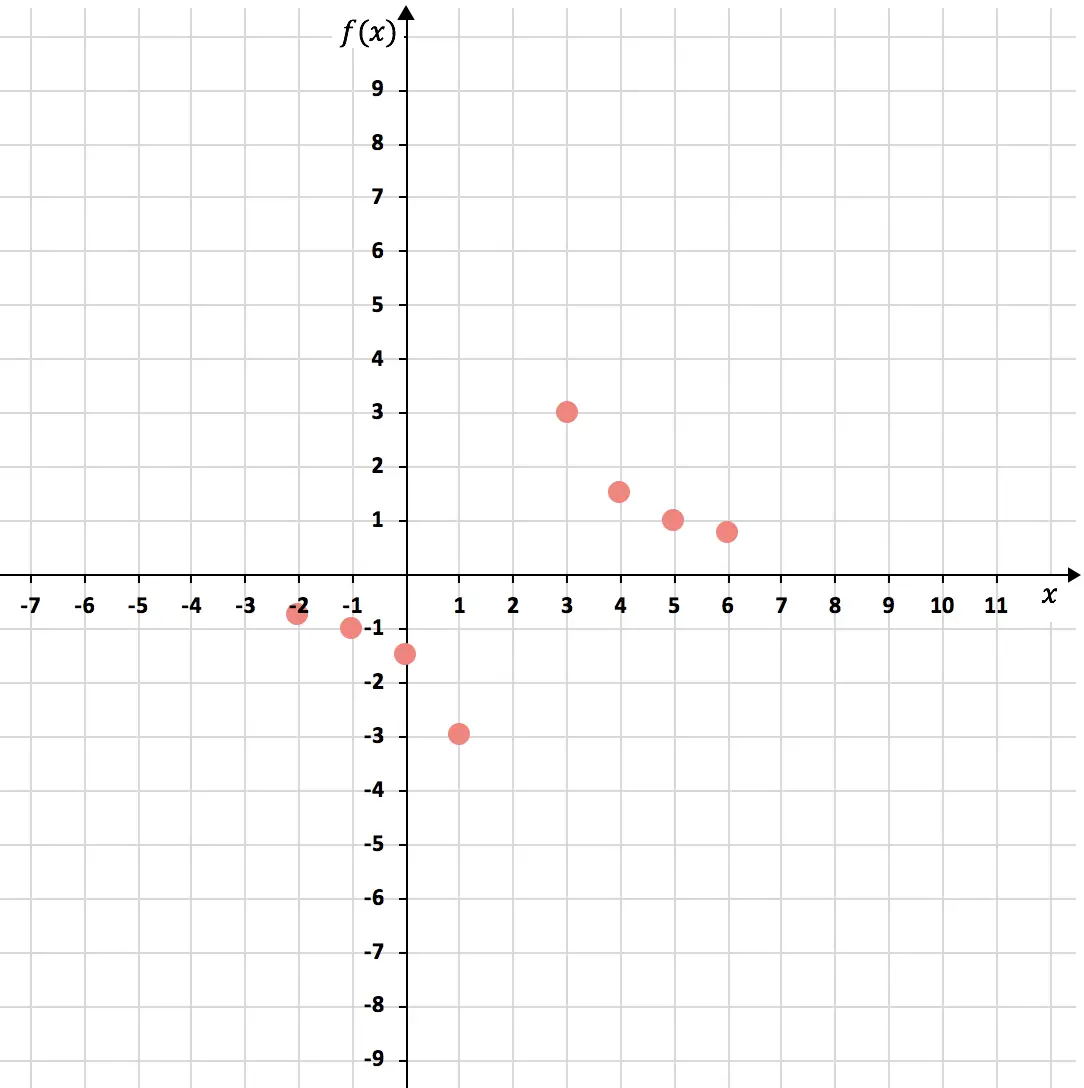
E infine uniamo i punti, formando le due iperboli della funzione di proporzionalità inversa. Inoltre, allunghiamo i rami delle iperboli per indicare che continuano a crescere:

Si noti che la funzione si approssima
![]()
, sia a destra che a sinistra. Tuttavia, non arriva mai a 2, ci arriva molto vicino ma non lo colpisce mai. COSÌ,
![]()
è un asintoto verticale . È perchè
![]()
non appartiene al dominio della funzione e, pertanto, la funzione in quel punto non esiste.
E la stessa cosa accade con l’asse X orizzontale. La funzione si avvicina
![]()
ma non toccarlo mai. Ancora,
![]()
è un asintoto orizzontale .
Ciò significa che tutte le funzioni di proporzionalità inversa sono discontinue, perché hanno sempre un asintoto.
Puoi saperne di più sugli asintoti e sui limiti delle funzioni sul nostro sito web.
Risolti problemi di funzioni di proporzionalità inversa
Esercizio 1
Calcolare il dominio della seguente funzione di proporzionalità inversa:
![]()
Una funzione di proporzionalità inversa non esisterà quando il denominatore è 0, perché in tal caso la funzione produrrebbe ∞. Dobbiamo quindi porre il denominatore della funzione uguale a 0 per vedere che x annulla il denominatore e, quindi, non appartiene al dominio.
![]()
![]()
![]()
![]()
Esercizio 2
Rappresentare graficamente la seguente funzione di proporzionalità inversa:
![]()
La prima cosa da fare è calcolare il dominio della funzione:
![]()
![]()
Una volta che sappiamo quale numero non appartiene al dominio, creiamo un array di valori con la funzione:

Infine rappresentiamo i punti ottenuti sul grafico e disegniamo le iperboli, formando così la funzione di proporzionalità inversa:
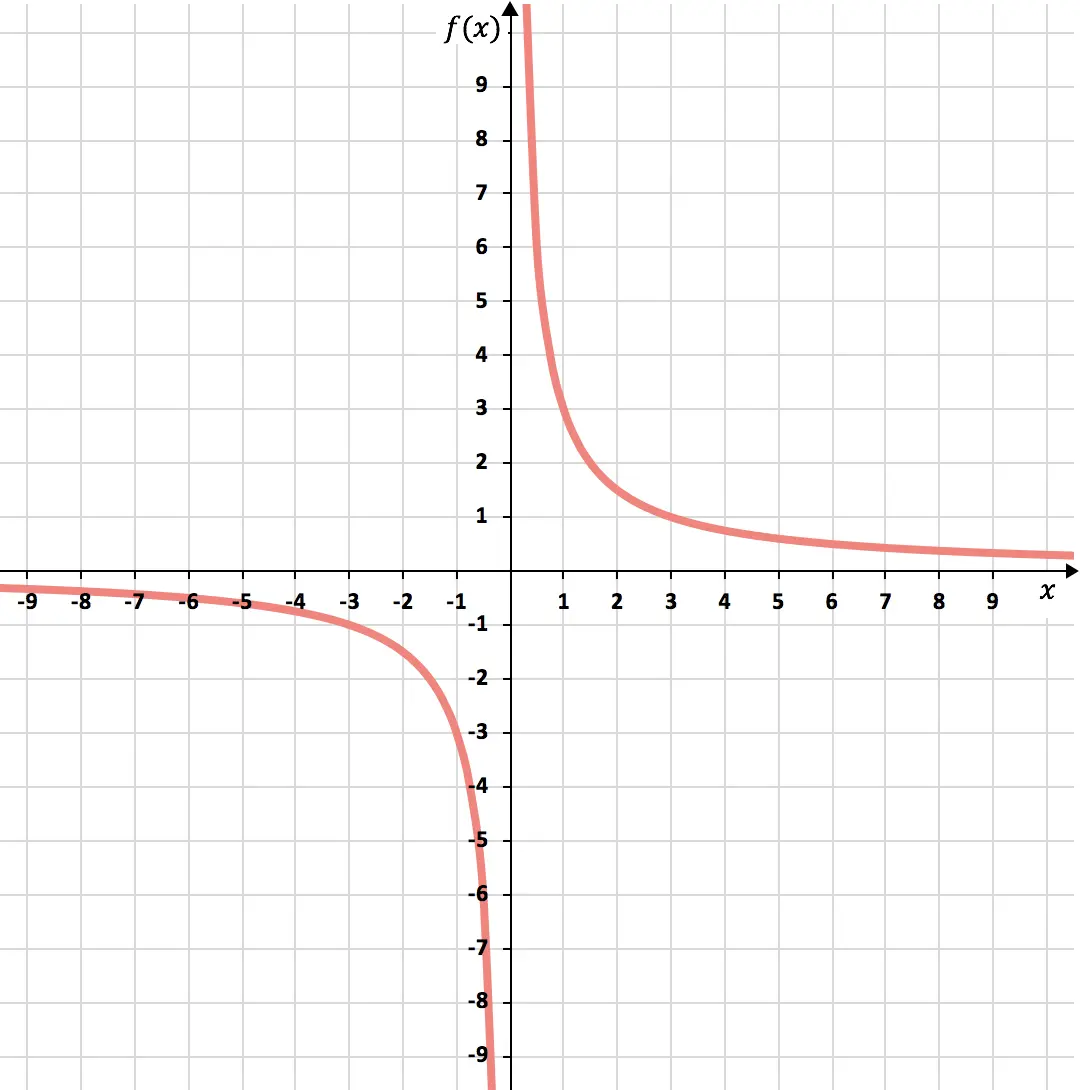
Esercizio 3
Rappresentare graficamente la seguente funzione di proporzionalità inversa:
![]()
La prima cosa da fare è calcolare il dominio della funzione:
![]()
![]()
![]()
Una volta conosciuto il dominio della funzione, costruiamo una tabella di valori:

Infine rappresentiamo i punti ottenuti su un grafico e tracciamo le iperboli, formando così la funzione di proporzionalità inversa:
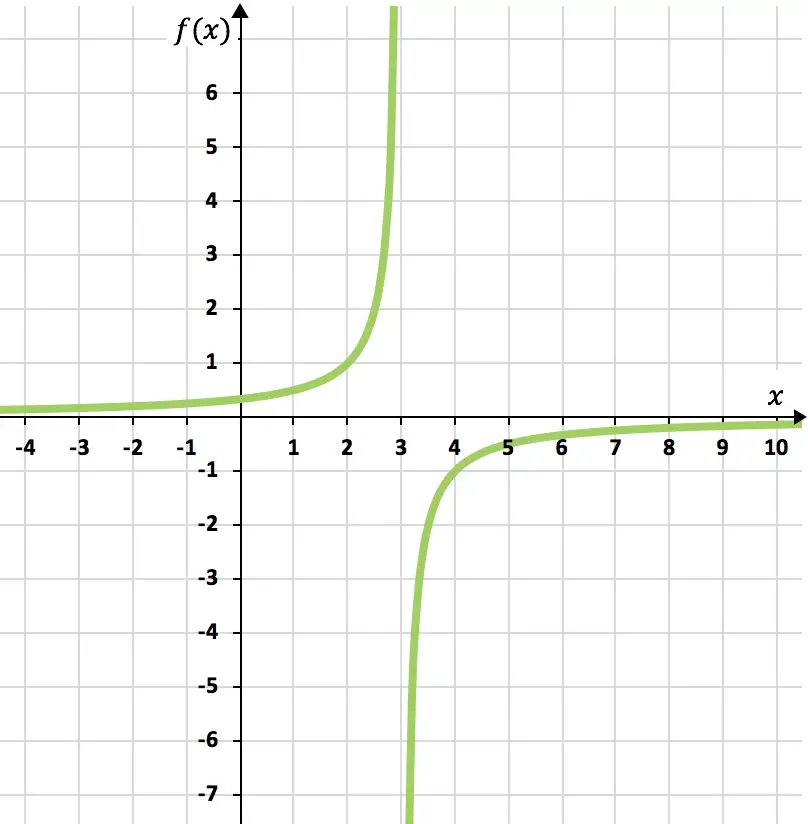
Esercizio 4
Rappresentare graficamente la seguente funzione di proporzionalità inversa:
![]()
Per prima cosa dobbiamo calcolare il dominio della funzione:
![]()
![]()
![]()
![]()
Una volta conosciuto il dominio della funzione, creiamo un array di valori:
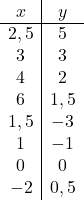
E, infine, rappresentiamo i punti ottenuti su un grafico e disegniamo le iperboli, formando così la funzione di proporzionalità inversa:
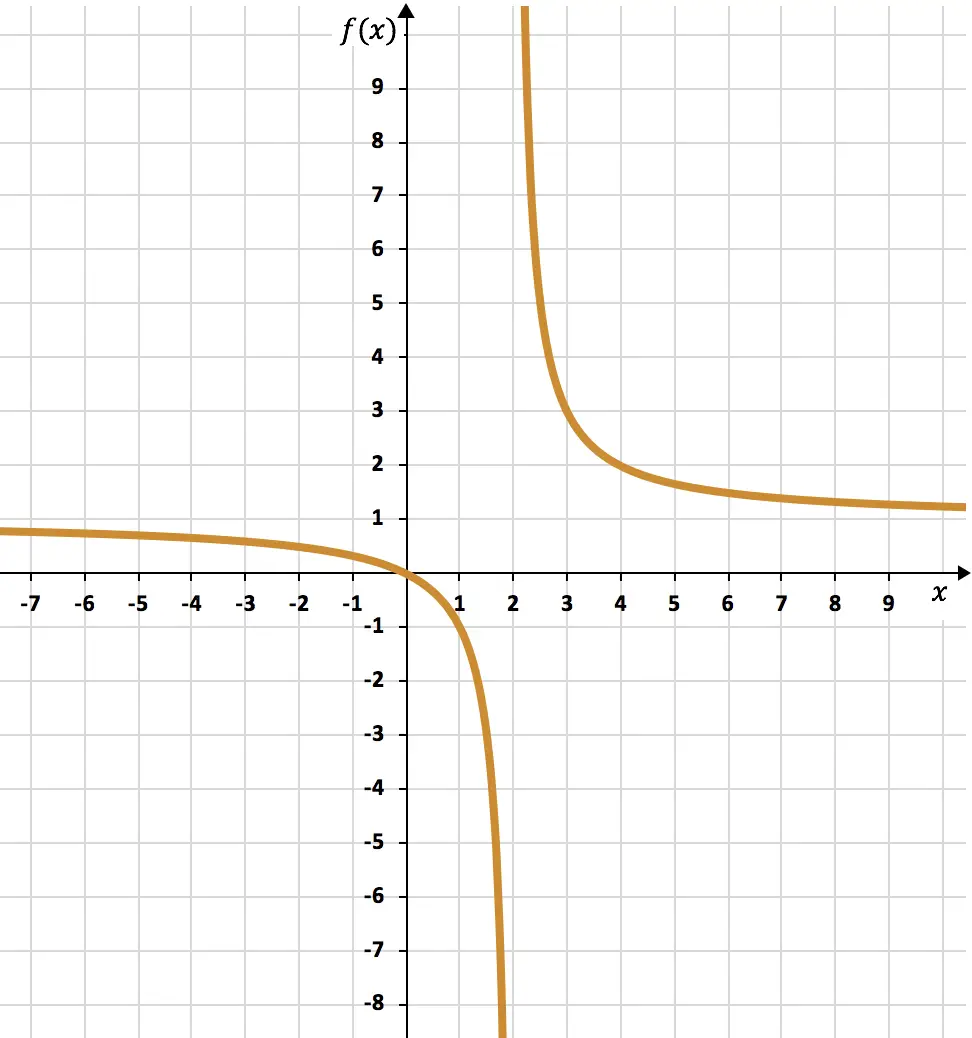
Esercizio 5
Rappresentare graficamente la seguente funzione razionale:
![]()
La prima cosa da fare è calcolare il dominio della funzione:
![]()
![]()
![]()
![]()
Una volta conosciuto il dominio della funzione, costruiamo una tabella di valori:

Per finire basta rappresentare su un grafico i punti ottenuti e disegnare le iperboli, formando così la funzione frazionaria:

Applicazioni della funzione di proporzionalità inversa
La funzione di proporzionalità inversa appare in molti casi in fisica e matematica.
Ad esempio, viene utilizzato per descrivere la relazione tra pressione e volume in un gas ideale sottoposto a una temperatura costante k. Questa funzione è chiamata legge di Boyle-Mariotte (P×V=k) ed è un esempio di funzione di proporzionalità inversa. Ovviamente il dominio di definizione di questa funzione è limitato al solo ramo positivo, non essendoci volumi o pressioni negative.
Anche il rapporto tra intensità di corrente e resistenza elettrica soggetta a differenza di potenziale costante è governato da una funzione di proporzionalità inversa. Questa funzione è nota come legge di Ohm (V=I×R).