In questa pagina spieghiamo cosa sono le matrici idempotenti. Ti mostriamo anche diversi esempi di questo tipo di matrici in modo che tu possa comprenderlo completamente. Inoltre troverai la formula per trovare una matrice idempotente e, infine, tutte le proprietà delle matrici idempotenti.
Cos’è una matrice idempotente?
La definizione di matrice idempotente è la seguente:
Una matrice idempotente è quella matrice che, moltiplicata per se stessa, dà come risultato la stessa matrice.
![]()
Pertanto, qualsiasi potenza di una matrice idempotente è uguale alla matrice stessa, indipendentemente dall’esponente:
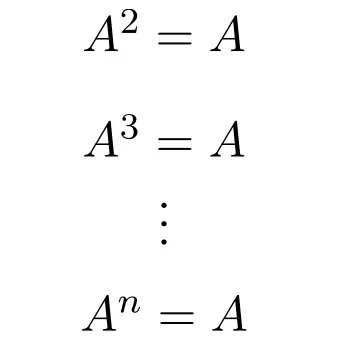
In effetti, questo è il motivo per cui questo tipo di tavola ha preso il nome. Perché in matematica l’idempotenza è un’operazione grazie alla quale otteniamo sempre lo stesso risultato indipendentemente dal numero di volte in cui viene eseguita.
Esempi di matrici idempotenti
Una volta conosciuto il concetto di matrice idempotente, vedremo alcuni esempi di diverse dimensioni per completare la sua comprensione.
Esempio di matrice idempotente 2×2
La seguente matrice quadrata di dimensione 2×2 è idempotente:
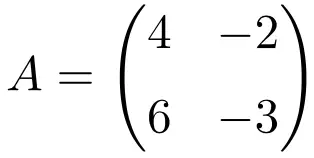
Per verificare che si tratta di una matrice idempotente, calcoliamo il suo quadrato:
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d83fda6875c8447818921c12f3196a7b_l3.png)
Il risultato è identico, dimostriamo quindi che si tratta di una matrice idempotente.
Esempio di matrice idempotente 3×3
La seguente matrice quadrata di dimensione 3×3 è idempotente:
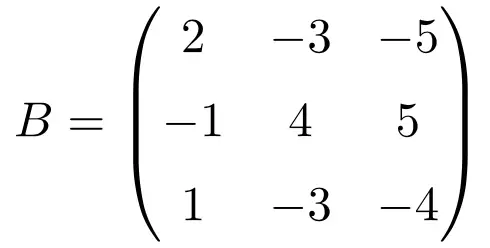
Per verificare che corrisponda una matrice idempotente, eleviamo la matrice a 2:
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-49a3f48608f3126039c949cde6346acf_l3.png)
Il risultato è lo stesso della matrice originale, quindi l’idempotenza della matrice è dimostrata.
Struttura di una matrice idempotente 2×2
Qui vi mostriamo la formula per ottenere una matrice idempotente. Nel caso fossi più interessato, puoi vedere la dimostrazione della formula qui sotto nei commenti, ma è un po’ noiosa quindi qui ti lasciamo direttamente con la formula per le matrici idempotenti :

In modo tale che gli elementi della diagonale secondaria di una matrice idempotente possono essere arbitrari purché la condizione sia soddisfatta
![]()
e i numeri sulla diagonale principale devono essere
![]()
E
![]()
Oltre a tutte le matrici descritte da questa formula, dobbiamo aggiungere la matrice Identità, anch’essa una matrice idempotente sebbene non rispetti la formula. Se non sai cos’è l’array, puoi chiedere cos’è l’array Identity .
Proprietà delle matrici idempotenti
Le matrici idempotenti hanno le seguenti caratteristiche:
- Il determinante di una matrice idempotente è sempre 0 o 1.
- Ad eccezione della matrice identità, tutte le altre matrici idempotenti sono entrambe matrici singolari o degeneri, cioè non sono invertibili.
- Qualsiasi matrice idempotente è diagonalizzabile e i suoi autovalori (o autovalori) sono sempre 0 o 1.
- La traccia di una matrice idempotente è uguale al rango della matrice.
- Esiste infine una relazione tra matrici idempotenti e matrici involutive: la matrice

è idempotente se e solo se la matrice
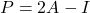
è involutivo.