Derivato del coseno

Qui scoprirai come derivare la funzione coseno (formula). Potrai vedere esempi di derivate di funzioni coseno ed esercitarti con esercizi passo passo. Inoltre, ti mostriamo la dimostrazione della formula, qual è la derivata seconda del coseno e anche la derivata dell’inverso del coseno.

Qual è la derivata del coseno?

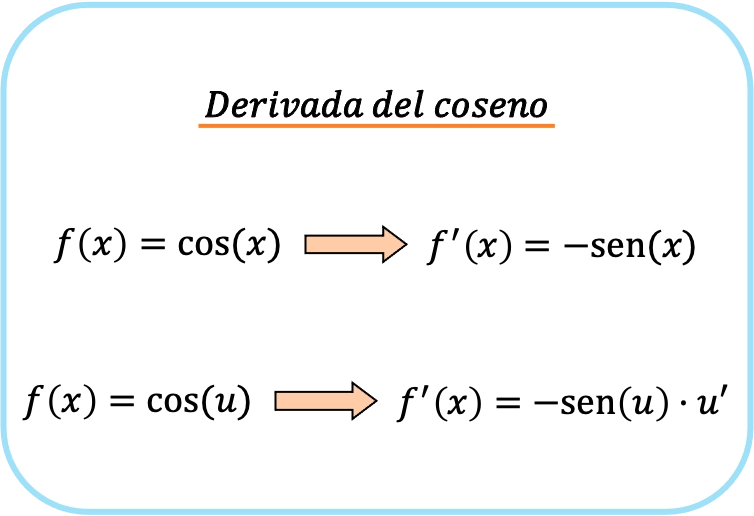
La derivata della funzione coseno è la funzione seno con segno modificato. In altre parole, la derivata del coseno di x è uguale a meno il seno di x.

f(x)=\text{cos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x)

Se è presente una funzione nell’argomento coseno, la derivata del coseno è il prodotto di meno il seno di quella funzione per la derivata della funzione.

f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'

La seconda formula è equivalente alla prima formula ma applica la regola della catena. Quindi, in sintesi, la formula per la derivata del coseno è la seguente:

derivata del coseno

Esempi di derivata del coseno

Ora che sappiamo cos’è la formula del coseno, spiegheremo diversi esempi di questo tipo di derivate trigonometriche in modo che tu non abbia dubbi su come derivare la funzione coseno.

Esempio 1: Derivata del coseno di 2x

f(x)=\text{cos}(2x)

Nell’argomento coseno non abbiamo una singola x, ma piuttosto una funzione più complessa. Pertanto, dobbiamo utilizzare la seguente formula per ricavare il coseno:

f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'

Poiché la derivata di 2x è 2, la derivata del coseno di 2x sarà meno il seno di 2x moltiplicato per 2.

f(x)=\text{cos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(2x)\cdot 2=-2\text{sen}(2x)

Esempio 2: Derivata del coseno di x al quadrato

f(x)=\text{cos}(x^2)

Come nell’esempio precedente, nell’argomento coseno abbiamo una funzione diversa da x, quindi utilizzeremo la regola della catena per ricavare il coseno:

f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'

Allora la derivata di x 2 è 2x, quindi la derivata del coseno di x elevata a 2 è:

f(x)=\text{cos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x^2)\cdot 2x

Esempio 3: Derivata del coseno al cubo

f(x)=\text{cos}^3(2x^6-5x^3)

La funzione coseno in questo esempio è composta da un’altra funzione, quindi dobbiamo applicare la seguente formula per risolvere la derivata:

f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'

Quindi, applicando la formula, arriviamo alla derivata della funzione:

\begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}

➤ Per differenziare questa funzione è necessario utilizzare anche la formula per la derivata di una funzione potenziale .

Derivata seconda del coseno

Successivamente vedremo che la derivata seconda del seno può essere facilmente calcolata, grazie alle caratteristiche delle funzioni trigonometriche.

➤ Nota: per comprendere quanto segue, è necessario sapere qual è la derivata del seno .

La derivata seconda del coseno di x è meno il coseno di x. Questo può sembrare strano, ma matematicamente è così. Infatti la derivata del seno è il coseno e, quindi, differenziando due volte il coseno di x, si ottiene nuovamente il coseno ma con segno modificato.

\begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}

Questa proprietà cambia se l’argomento coseno non è x, poiché in questo caso trasciniamo il termine della regola della catena:

\begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}

Derivata del coseno inverso

Tutte le funzioni trigonometriche hanno una funzione inversa e come tale anche la funzione coseno può essere invertita. Allo stesso modo, l’inverso del coseno è differenziabile.

La derivata dell’inverso del coseno di una funzione è meno la derivata della funzione divisa per la radice quadrata di uno meno il quadrato di detta funzione.

f(x)=\text{cos}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}

Ricorda che il coseno inverso è anche chiamato arcocoseno.

Ad esempio, la derivata dell’inverso del coseno di 3x è:

f(x)=\text{cos}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{3}{\sqrt{1-(3x)^2}}=-\cfrac{3}{\sqrt{1-9x^2}}

Esercizi risolti sulla derivata del coseno

Calcola la derivata delle seguenti funzioni coseno:

\text{A) } f(x)=\text{cos}(4x)

\text{B) } f(x)=\text{cos}(2x^3-5x+1)

\text{C) } \displaystyle f(x)=9\text{cos}\left(\frac{x}{3}\right)

\text{D) } f(x)=\text{cos}^5(x^2+3x)

\text{E) } f(x)=\text{cos}\left(e^{5x}\right)

\text{F) } \displaystyle f(x)=9\text{cos}\left(\frac{e^x}{5x}\right)

\text{A) } f'(x)=-\text{sen}(4x)\cdot 4 =-4\text{sen}(4x)

\text{B) } f'(x)=-\text{sen}(2x^3-5x+1)\cdot (6x^2-5)

\text{C) } \displaystyle f'(x)=-9\text{sen}\left(\frac{x}{3}\right)\cdot \frac{1}{3} =-3\text{sen}\left(\frac{x}{3}\right)

\text{D) } f'(x)=-5\text{cos}^4(x^2+3x)\cdot \text{sen}(x^2+3x)\cdot (2x+3)

\text{E) } f'(x)=-\text{sen}\left(e^{5x}\right)\cdot e^{5x}\cdot 5=-5\text{sen}\left(e^{5x}\right)\cdot e^{5x}

\begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}

Dimostrazione della derivata del coseno

Infine, dimostreremo matematicamente la formula per la derivata del coseno di x. Per fare ciò utilizzeremo la definizione di derivata, che corrisponde al seguente limite:

\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}

Dimostreremo il coseno, quindi la funzione è cos(x):

\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x+h)-\text{cos}(x)}{h}

Non possiamo risolvere questo limite mediante la sostituzione, perché finiremmo nell’indeterminatezza. Possiamo però esprimere il coseno di una somma in un altro modo applicando la seguente identità trigonometrica:

\text{cos}(a+b)=\text{cos}(a)\text{cos}(b)-\text{sen}(a)\text{sen}(b)

\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x)\text{cos}(h)-\text{sen}(x)\text{sen}(h)-\text{cos}(x)}{h}

Il prossimo passo è separare la frazione in due frazioni e prendere il fattore comune del coseno:

\displaystyle f'(x)=\lim_{h \to 0}\left[\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\frac{\text{sen}(x)\text{sen}(h)}{h}\right]

Il limite di una sottrazione è uguale alla sottrazione dei limiti, quindi:

\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\lim_{h \to 0}\frac{\text{sen}(x)\text{sen}(h)}{h}

Il coseno di x e il seno di x non dipendono da h, quindi possiamo estrarli fuori dai limiti:

\displaystyle f'(x)=\text{cos}(x)\lim_{h \to 0}\frac{\text{cos}(h)-1}{h}-\text{sen}(x)\lim_{h \to 0}\frac{\text{sen}(h)}{h}

Utilizzando il calcolo dei limiti per equivalenti infinitesimi, concludiamo che il primo limite è 0 e il secondo limite è 1. Pertanto:

\displaystyle f'(x)=\text{cos}(x)\cdot 0-\text{sen}(x)\cdot 1

\displaystyle f'(x)=-\text{sen}(x)

E abbiamo già raggiunto la formula per la derivata della funzione coseno, quindi l’uguaglianza è dimostrata.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto