In questa pagina troverai cos’è una matrice scalare e diversi esempi di matrici scalari per comprenderla perfettamente. Inoltre, potrai vedere tutte le proprietà delle matrici scalari e i vantaggi di eseguire operazioni con esse. Infine, spieghiamo come calcolare il determinante di una matrice scalare e come invertire questo tipo di matrice.
Cos’è una matrice scalare?
Una matrice scalare è una matrice diagonale in cui tutti i valori sulla diagonale principale sono uguali.
Questa è la definizione di matrice scalare, ma sono sicuro che si capisca meglio con degli esempi: 😉
Esempi di array scalari
Esempio di matrice scalare di ordine 2×2
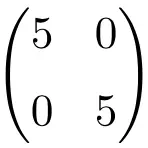
Esempio di matrice scalare 3×3
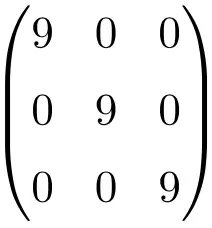
Esempio di matrice scalare di dimensione 4×4
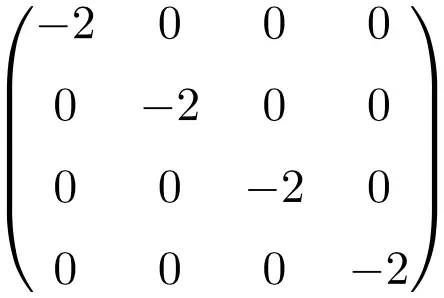
Proprietà delle matrici scalari
La matrice scalare è anche una matrice diagonale, quindi vedrai che eredita molte caratteristiche di questa classe di matrici:
- Tutte le matrici scalari sono anche matrici simmetriche .
- Una matrice scalare è sia una matrice triangolare superiore che una matrice triangolare inferiore .
- La matrice identità è una matrice scalare.
- Qualsiasi matrice scalare può essere ottenuta dal prodotto di una matrice identità e un numero scalare.
![Rendered by QuickLaTeX.com 4 \cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b77f7d177c2769b0847de258adfd1386_l3.png)
- La matrice zero è anche una matrice scalare.
- Gli autovalori (o autovalori) di una matrice scalare sono gli elementi della sua diagonale principale. Pertanto i loro autovalori saranno sempre gli stessi e si ripeteranno tante volte quanto è la dimensione della matrice.
![Rendered by QuickLaTeX.com \begin{pmatrix} 8 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \longrightarrow \ \lambda = 8 \ ; \ \lambda = 8 \ ; \ \lambda = 8](https://mathority.org/wp-content/ql-cache/quicklatex.com-2513b8d4aeb6d932d9870934102a1637_l3.png)
- L’aggiunto di una matrice scalare è un’altra matrice scalare. Inoltre, i valori della diagonale principale della matrice allegata saranno sempre quelli della matrice originaria elevati all’ordine della matrice – 1 .
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \longrightarrow \text{Adj}(A)=\begin{pmatrix} 5^{3-1} & 0 & 0 \\[1.1ex] 0 & 5^{3-1} & 0 \\[1.1ex] 0 & 0 & 5^{3-1} \end{pmatrix}= \begin{pmatrix} 25 & 0 & 0 \\[1.1ex] 0 & 25 & 0 \\[1.1ex] 0 & 0 & 25 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f7e94cc5a528abace04016dc263c8f9_l3.png)
Operazioni con matrici scalari
Uno dei motivi per cui le matrici scalari sono così ampiamente utilizzate nell’algebra lineare è la facilità con cui consentono di eseguire calcoli. Ecco perché sono così importanti in matematica.
Vediamo allora perché è così semplice fare calcoli con questo tipo di matrice quadrata:
Addizione e sottrazione di matrici scalari
Aggiungere (e sottrarre) due matrici scalari è molto semplice: basta aggiungere (o sottrarre) i numeri sulle diagonali principali. Per esempio:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} +\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix} = \begin{pmatrix} 7& 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-761de4b4c9bdbbc835b366b21d8cfc2d_l3.png)
Moltiplicazione di matrici scalari
Similmente all’addizione e alla sottrazione, per risolvere una moltiplicazione o un prodotto matriciale tra due matrici scalari, è sufficiente moltiplicare gli elementi delle diagonali tra di loro. Per esempio:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \cdot\begin{pmatrix} 6 & 0 & 0 \\[1.1ex] 0 & 6 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 12 & 0 & 0 \\[1.1ex] 0 & 12 & 0 \\[1.1ex] 0 & 0 & 12 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d30acbf9c6ad31625f8253549e659b02_l3.png)
Potenze di matrici scalari
Anche calcolare la potenza di una matrice scalare è molto semplice: bisogna elevare ogni elemento della diagonale all’esponente. Per esempio:
*** QuickLaTeX cannot compile formula:
\displaystyle\left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}\right.^4=\begin{pmatrix} 2^ 4 & 0 & 0 \\[1.1ex] 0 & 2^
*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \right. inserted.
leading text: \end{document}
& 0 \\[1.1ex] 0 & 0 & 2^4 \end{pmatrix}= \begin{pmatrix} 16 & 0 & 0 \\[1.1ex] 0 & 16 & 0 \\[1.1ex] 0 & 0 e 16 \end{pmatrice}
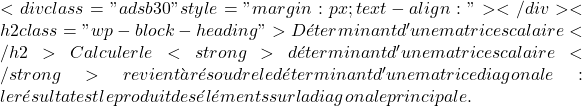
![]()
\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7 \cdot 7 \cdot 7 = \bm {343}
![]()
\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7^3= \bm{343}
![Démontrer ce théorème est très simple : il suffit de calculer le déterminant d'une matrice scalaire par blocs (ou cofacteurs). Vous trouverez ci-dessous la <strong>démonstration</strong> de la formule utilisant une matrice scalaire générique :” title=”Rendered by QuickLaTeX.com” height=”62″ width=”1060″ style=”vertical-align: -4px;”></p>
<p> \begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & a & 0 \\[1.1ex] 0 & 0 & a \end{vmatrix}& = a \cdot \begin{ vmatrix} a & 0 \\[1.1ex] 0 & a \end{vmatrix} – 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & a \end{vmatrix} + 0 \cdot \ Begin{vmatrix} 0 & a \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (a\cdot a) – 0 \cdot 0 + 0 \cdot 0 \\[ 2ex] & = a \cdot a \cdot a \\[2ex] & = a^3 \end{aligned}</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-d24f9aa91fc9fe8ed74f705f83be3b32_l3.png)
![]()
un^3
![car la matrice est d'ordre 3, mais il faut toujours l'élever à l'ordre de la matrice.
<div class="adsb30" style=" margin:12px; text-align:center">
<div id="ezoic-pub-ad-placeholder-118"></div>
</div>
<h2 class="wp-block-heading"> Inverser une matrice scalaire</h2>
<p> Une matrice scalaire <strong>est inversible si, et seulement si, tous les éléments de la diagonale principale sont différents de 0</strong> . Dans ce cas on dit que la matrice scalaire est une matrice régulière. De plus, l’inverse d’une matrice scalaire sera toujours une autre matrice scalaire avec les <strong>inverses</strong> de la diagonale principale :” title=”Rendered by QuickLaTeX.com” height=”174″ width=”1250″ style=”vertical-align: -5px;”></p>
<p> \displaystyle A= \begin{pmatrix} 9 & 0 & 0 \\[1.1ex] 0 & 9 & 0 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} \ \longrightarrow \ A^{-1 }=\begin{pmatrix} \frac{1}{9} & 0 & 0 \\[1.1ex] 0 & \frac{1}{9} & 0 \\[1.1ex] 0 & 0 & \frac{ 1}{9} \end{pmatrice}</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-49f5afdd3e1e9918f5323139662a2138_l3.png)
![]()
\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{2} \cdot \cfrac{1}{2}=\cfrac{1}{8} = $0,125