In questa pagina troverai una spiegazione di cosa sono le linee simultanee, nonché esempi di linee simultanee.
Quali sono le linee concorrenti?
La definizione matematica di linee concorrenti è la seguente:
In geometria, le linee concorrenti sono due o più linee complanari che si intersecano nello stesso punto (chiamato punto di concorrenza). Pertanto un insieme di linee concorrenti ha un solo punto in comune.
Se lavoriamo nel piano (in R2) due rette diverse possono essere solo coincidenti, parallele o secanti. Quindi tutte le rette secanti sono anche rette concorrenti, poiché hanno un punto di intersezione .
Se il concetto precedente non ti è stato chiaro, ti consiglio di dare un’occhiata alla definizione di linee che si intersecano , dove troverai cosa sono questi tipi di linee e come sapere se due linee si intersecano oppure no.
Quando invece operiamo nello spazio (in R3) è più difficile trovare linee concorrenti, perché è più complicato che 2, 3, 4,… linee si intersechino nello stesso punto e, inoltre, siano contenute nello stesso punto stesso aereo.
D’altronde il concetto di competizione non si applica solo alle rette: se due o più oggetti geometrici diversi condividono un punto, significa che sono concorrenti.
Esempio di linee concorrenti
Una volta visto il significato delle linee concorrenti, vediamo ora un esempio di questo tipo di linee:
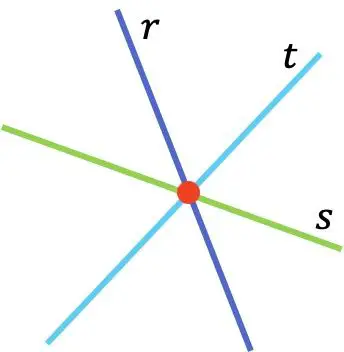
Come puoi vedere nella rappresentazione grafica delle linee r, s e t, le tre linee sono concorrenti perché si intersecano nello stesso punto (mostrato in rosso).
D’altra parte, prima di concludere, se ti è piaciuta questa pagina, forse ti interesseranno anche le linee rette in generale. Ebbene, un concetto molto importante riguardo alle linee è calcolare la loro equazione, infatti, nella geometria analitica, le equazioni delle linee vengono utilizzate molto spesso. Puoi vedere come appare questa equazione nella pagina successiva: Come calcolare l’ equazione della linea che passa per due punti .