In questa pagina imparerai cosa sono i vettori complanari e come capire se 2, 3, 4 o più vettori sono complanari. Inoltre, potrai vedere esempi ed esercizi risolti passo passo su vettori complanari.
Cosa sono i vettori complanari?
In geometria analitica, il significato dei vettori complanari (o complanari) è il seguente:
I vettori complanari sono vettori che appartengono allo stesso piano.
Pertanto, due vettori sono sempre complanari perché un piano può essere formato con un minimo di 2 vettori. Quando invece ci sono 3, 4 o più vettori, è possibile che uno dei vettori non sia contenuto nello stesso piano e, quindi, che non siano complanari.
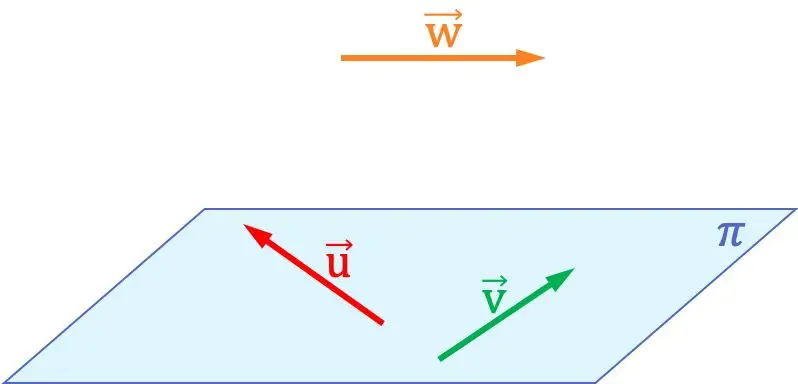
Ad esempio, nel grafico sopra puoi vedere che i vettori
![]()
E
![]()
sono complanari tra loro, poiché contenuti nello stesso piano. D’altra parte, questi due vettori non sono complanari al vettore
![]()
, perché nello spazio che contiene i tre vettori non si può formare alcun piano.
Da questa proprietà si deduce che se 3 o più vettori sono complanari, anche i punti che definiscono detti vettori (inizio e fine del vettore) sono punti complanari.
Quando i vettori sono complanari?
Come abbiamo visto nella definizione di vettori complanari (o complanari), due vettori sono sempre complanari, ma non è necessario che più di due vettori rispettino il rapporto di complanarità.
Pertanto, esistono diversi metodi per determinare se tre o più vettori sono complanari:
- Se il prodotto misto di tre vettori (o prodotto triplo punto) è uguale a zero, significa che i tre vettori sono complanari. Se non ti è molto chiaro come si calcola questa operazione, ti consiglio di dare un’occhiata a cos’è il prodotto misto di tre vettori , qui troverai la spiegazione nonchè esempi ed esercizi risolti.
![]()
- Se un insieme di vettori può essere espresso come combinazione lineare di due vettori, ciò implica che essi sono complanari, nel senso che 3 o più vettori sono complanari se e solo se sono linearmente dipendenti. Per dimostrare che tre o più vettori sono una combinazione lineare di due vettori è sufficiente che il rango della matrice formata da tutti i vettori sia pari a 2.
![]()
È importante comprendere bene il concetto di dipendenza e indipendenza lineare , ovvero quando due vettori sono linearmente dipendenti o linearmente indipendenti e cosa ciò significa. Se non ti è del tutto chiaro, nel link troverai una spiegazione molto dettagliata, dove, inoltre, potrai vedere esempi ed esercizi risolti passo dopo passo.
- Se i vettori in questione sono vettori paralleli , ciò significa che sono anche complanari, cioè tutti i vettori paralleli sono contenuti nello stesso piano.
![]()
Risolti problemi di vettori complanari
Esercizio 1
Determina se i seguenti tre vettori sono complanari:
![]()
![]()
![]()
Per verificare se si tratta di 3 vettori complanari, dobbiamo calcolare il prodotto misto tra i tre vettori:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a1e4b0655c0a3f0165c880f5e64cce0_l3.png)
Il prodotto misto dei tre vettori è zero, quindi i 3 vettori sono complanari .
Esercizio 2
Determina se i seguenti tre vettori sono complanari:
![]()
![]()
![]()
Un modo per verificare se abbiamo a che fare con 3 vettori complanari sarebbe risolvere il prodotto misto tra i tre vettori. Tuttavia, se osserviamo attentamente le componenti dei vettori, possiamo vedere che sono proporzionali. Pertanto i tre vettori sono paralleli tra loro.
![]()
E poiché tutti i vettori sono paralleli, sono effettivamente 3 vettori complanari .
Esercizio 3
Determina se i seguenti quattro vettori sono complanari:
![]()
![]()
![]()
![]()
Per sapere se i quattro vettori sono complanari dobbiamo calcolare il rango della matrice composta da tutti i vettori:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8384924c86edafd568505d5f80e1705d_l3.png)
In questo caso, calcoliamo la portata di detta matrice mediante determinanti:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-2778435c7f53952adf072419af8b268c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-82f278494a221879cc86da92ab4378c8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1 \\[1.1ex] 1&-1\end{vmatrix}= -3\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-889142ac348173dd6c838633007f2d06_l3.png)
![]()
Il rango della matrice formata da tutti i vettori è pari a 2, quindi i 4 vettori sono complanari .
Esercizio 4
Calcolare il valore del parametro
![]()
in modo che i seguenti 4 punti siano complanari:
![]()
![]()
![]()
![]()
Affinché i quattro punti siano complanari, i vettori da essi determinati devono essere complanari. Calcoliamo quindi questi vettori:
![]()
![]()
![]()
La cui matrice vettoriale è:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3d801efcf5b56dd858890720797d6a4_l3.png)
Affinché i vettori risultanti siano complanari, il rango della matrice deve essere 2. E, quindi, il determinante dell’intera matrice 3×3 deve essere 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bb7d3b31c10096d100843d781a85b621_l3.png)
![]()
Infine, risolviamo l’ignoto
![]()
![]()
![]()