In questa pagina scoprirai cosa significa quando due linee sono complanari. Potrai anche vedere quando due linee sono complanari e, inoltre, troverai esempi ed esercizi risolti di linee complanari.
Cosa sono due linee complanari?
In geometria analitica, la definizione di rette complanari è la seguente:
Due rette sono complanari quando si trovano sullo stesso piano. Pertanto, le linee complanari possono essere solo linee secanti , linee parallele o linee coincidenti .
Inoltre bastano due linee complanari per definire completamente un piano. Anche se ovviamente un piano può avere più di due rette complanari, in realtà ogni piano contiene un numero infinito di rette.
D’altra parte, se due rette non sono complanari significa che si intersecano.
Esempi di linee complanari
Per farti comprendere meglio il concetto di linee complanari, ecco un esempio con tre linee:
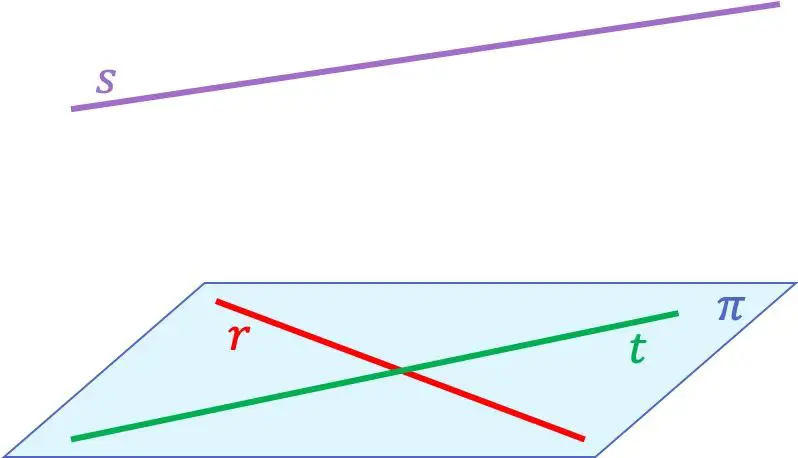
In questo caso, le linee
![]()
E
![]()
Sono complanari perché appartengono allo stesso piano. Invece la linea retta
![]()
non è complanare con nessuna delle altre due rette, poiché le interseca
![]()
E
![]()
Come fai a sapere se due linee sono complanari?
Come abbiamo visto sopra nella spiegazione delle rette complanari, queste possono essere solo rette secanti, parallele o coincidenti. In altre parole, 2 linee incrociate non saranno mai complanari.
Pertanto, per sapere se due linee sono complanari occorre determinare la posizione relativa tra loro, e se si tratta di due linee che si intersecano, parallele o coincidenti, ciò significa che sono linee complanari.
Quindi, per verificare la complanarità di due linee, bisogna prima sapere come calcolare la posizione relativa di due linee nello spazio . Se ancora non avete familiarità con questo concetto, è meglio dare prima un’occhiata al link, dove troverete la spiegazione completa oltre ad esempi, esercizi e problemi risolti.
Esercizio risolto di linee complanari
A titolo di esempio risolveremo un tipico esercizio su rette complanari:
- Determina se le seguenti due linee sono complanari o meno:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=4t \\[1.7ex] z=5 \end{cases} \qquad \qquad s : \ \begin{cases} 2x+y=0 \\[1.7ex] z=-2\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76e57f7dd2bfa67f2cf4eb2ee0455dcf_l3.png)
La prima cosa che dobbiamo fare è trovare la posizione relativa tra le due linee e, per questo, dobbiamo averle entrambe espresse con lo stesso tipo di equazione. Quindi attraverseremo la linea retta
![]()
dall’equazione generale (o implicita) alle equazioni parametriche:
![Rendered by QuickLaTeX.com \displaystyle s : \ \begin{cases} 2x+y=0 \\[1.7ex] z=-2\end{cases} \xrightarrow{x \ = \ t} \ \begin{cases} 2t+y=0 \\[1.7ex] z=-2\end{cases} \longrightarrow \ \begin{cases} x=t \\[1.7ex] y=-2t \\[1.7ex] z=-2\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d8dbc805cb7e0020c9c82c90e56e011_l3.png)
Quindi il vettore direzione di ciascuna linea è:
![]()
Le coordinate dei vettori di direzione delle due rette sono proporzionali, quindi possono essere solo rette coincidenti o parallele. Pertanto in questo caso particolare non è necessario calcolare l’esatta posizione relativa, poiché le linee parallele e le linee coincidenti sono linee complanari. Quindi le due rette sono complanari .