Calcola il punto di intersezione o intersezione tra due linee

Qui troverai come viene calcolato il punto di taglio (o intersezione) tra due linee. Vedrai anche degli esempi e potrai esercitarti con esercizi risolti passo dopo passo.

Qual è il punto di interruzione o di intersezione tra due linee?

Il punto di intersezione (o taglio) tra due linee è il punto in cui si incrociano due linee diverse. Pertanto, quando due linee diverse hanno un punto di intersezione o di taglio, significa che coincidono in un punto.

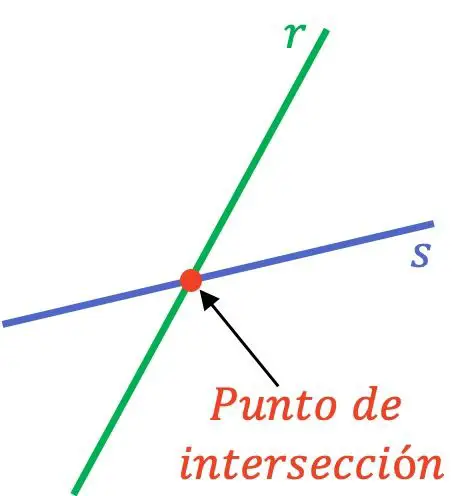
Perché due linee si intersechino in un punto, devono essere linee intersecanti, poiché le linee parallele non si toccano in nessun punto.

Se non ricordi esattamente cosa sono le linee che si intersecano, ti consigliamo di consultare la nostra pagina Esempi di linee che si intersecano , dove troverai una spiegazione dettagliata di cosa sono questi tipi di linee e come capire se due linee si intersecano o meno.

Come calcolare il punto di interruzione o di intersezione tra due linee?

Una volta vista la definizione del punto di intersezione o intersezione tra due linee, vediamo ora come viene calcolato detto punto.

Per trovare il punto di intersezione (o intersezione) tra due linee, bisogna innanzitutto assicurarsi che le due linee non siano parallele, perché se sono due linee parallele non si intersecheranno in nessun punto. Pertanto, bisogna prima sapere come determinare quando due rette sono parallele e quando non lo sono; Se non ricordi come si fa, puoi guardarlo di nuovo cliccando sul link.

Una volta che sappiamo che le due rette non sono parallele, per determinare il punto di intersezione (o intersezione) tra le due rette, dobbiamo risolvere il sistema di equazioni formato dall’equazione di ciascuna retta. E il risultato di detto sistema di equazioni saranno le coordinate del punto di intersezione (o intersezione) tra le due linee.

Esempio di come trovare il punto di intersezione o intersezione tra due linee

Ad esempio, risolveremo un problema in modo che tu possa vedere come trovare il punto di intersezione (o intersezione) tra 2 linee:

• Trova il punto di intersezione tra le due linee seguenti:

Innanzitutto le rette non sono parallele perché hanno pendenze diverse, quindi si intersecano entrambe in un punto del piano cartesiano.

Per scoprirlo dobbiamo risolvere il sistema di equazioni composto dall’equazione di ciascuna retta:

In questo caso particolare, risolveremo il sistema con il metodo dell’equalizzazione a partire dalle due incognite

sono già risolti (entrambe le linee sono in forma di equazione esplicita):

Cancelliamo il valore della variabile

E una volta che sai quanto vale

Sostituiamo il suo valore in qualsiasi equazione per trovare il valore di

Pertanto le coordinate del punto di intersezione tra le due rette sono:

Risolti problemi di punto di intersezione o intersezione tra due linee

Esercizio 1

Qual è il punto di intersezione o di intersezione tra le seguenti due rette?

Innanzitutto, le linee non sono parallele perché hanno pendenze diverse, quindi le due linee si incontreranno in un punto del piano.

Per calcolare tale punto è necessario risolvere il sistema di equazioni formato dall’equazione di ciascuna retta:

In questo caso risolveremo il sistema di equazioni con il metodo dell’equalizzazione a partire dalle due incognite

sono già risolti (entrambe le linee sono in forma di equazione esplicita):

Cancelliamo il valore della variabile

E una volta che sai quanto vale

Sostituiamo il suo valore in qualsiasi equazione per trovare il valore di

Le coordinate del punto di intersezione tra le due linee sono quindi:

Esercizio 2

Trova il punto di intersezione o intersezione tra le seguenti due linee:

la destra

È espresso sotto forma di un’equazione implicita (o generale), quindi lo passeremo prima sotto forma di un’equazione esplicita per conoscere il valore della sua pendenza:

Quindi le due rette hanno pendenze diverse e quindi esiste un punto di intersezione tra loro.

Per calcolare tale punto è necessario risolvere il sistema di equazioni formato dall’equazione di ciascuna retta:

Risolviamo il sistema di equazioni con il metodo di equalizzazione:

Cancelliamo il valore della variabile

E una volta che sai quanto vale

Sostituiamo il suo valore in entrambe le equazioni per trovare il valore di

Le coordinate del punto di intersezione tra le due linee sono quindi:

Esercizio 3

Determinare il punto di intersezione o intersezione tra le seguenti due linee:

Innanzitutto bisogna sapere se si tratta di due rette parallele oppure no. Per fare ciò vedremo se i vettori di direzione delle due rette sono proporzionali.

la destra

è definito sotto forma di equazioni parametriche, quindi le componenti del suo vettore di direzione sono i coefficienti davanti al parametro

E, d’altra parte, la linea

è descritto sotto forma di un’equazione implicita, quindi il suo vettore di direzione è:

Sicché le componenti dei due vettori di direzione non sono proporzionali tra loro, le due rette non sono quindi parallele.

E poiché le due rette non sono parallele, ciò implica che esista effettivamente un punto di intersezione tra loro. Per calcolarlo, dobbiamo risolvere il sistema di equazioni formato dall’equazione di ciascuna linea:

In questo caso, come la linea

è sotto forma di equazioni parametriche, è necessario sostituire l’espressione di ciascuna equazione parametrica nell’equazione dell’altra riga:

Ora risolviamo l’equazione risultante:

e sostituire il valore di

trovato nelle equazioni parametriche per trovare le coordinate del punto di taglio:

Quindi il punto di intersezione tra le due rette è: