Distanza da un punto a un piano nello spazio (formula)

In questa pagina troverai come viene calcolata la distanza tra un punto e un piano nello spazio (formula). Inoltre, potrai vedere esempi ed esercitarti con esercizi risolti passo dopo passo.

Qual è la distanza da un punto a un piano?

Nella geometria analitica, la distanza da un punto a un piano è la distanza più breve tra il punto e qualsiasi altro punto sul piano. Questa distanza corrisponde alla lunghezza del segmento perpendicolare al piano che va dal punto al piano.

Formula per la distanza da un punto a un piano

Una volta vista esattamente la nozione di distanza tra un punto e un piano, vediamo ora la formula per calcolare tale distanza:

Dato un punto e l’equazione generale (o implicita) di un piano:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

La formula per la distanza da un punto a un piano è:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

La dimostrazione della formula per la distanza da un punto a un piano è piuttosto noiosa e lunga, quindi non la faremo in questa pagina.

Se invece applicando la formula otteniamo un risultato pari a zero, ciò significa ovviamente che la distanza tra il punto e il piano è zero e, quindi, il punto fa parte di quel piano.

Si noti infine che per applicare la formula, il piano deve essere definito come un’equazione generale (o implicita). Quindi se fosse espressa da un altro tipo di equazione piana, dovremmo prima trasformarla in un’equazione generale e poi utilizzare la formula.

Esempio di calcolo della distanza da un punto a un piano

Affinché tu possa vedere come viene determinata numericamente la distanza tra un punto e un piano, risolveremo un esempio di seguito:

Calcola la distanza tra il punto P e il piano π. Detto punto e piano:

$P(1,3,-2) \qquad \qquad \pi: \ 2x+5y-4z+7=0$

Per trovare la distanza dal punto al piano è sufficiente applicare la formula vista nella sezione precedente:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Ora sostituiamo il valore di ciascuna incognita nella formula:

$d(P,\pi) = \cfrac{\lvert 2\cdot 1+5\cdot 3-4\cdot (-2)+7\rvert}{\sqrt{2^2+5^2+(-4)^2}}$

E, infine, eseguiamo le operazioni:

$d(P,\pi) = \cfrac{\lvert 2+15+8+7\rvert}{\sqrt{4+25+16}}$

$\bm{d(P,\pi) = }\cfrac{\bm{32}}{\bm{\sqrt{45}}}$

Nota che al numeratore della frazione c’è un valore assoluto e al denominatore abbiamo una radice quadrata, quindi il risultato deve essere sempre positivo. Ciò ha senso perché le distanze non possono essere negative, ma sono sempre positive.

Calcola la distanza tra due piani paralleli

Due piani paralleli sono sempre alla stessa distanza, quindi, per trovare la distanza tra due piani paralleli, possiamo prendere un punto su uno dei due piani e calcolare la distanza da quel punto all’altro piano.

È un metodo per trovare la distanza tra due piani paralleli. Esiste però un modo ancora più semplice per farlo quando i coefficienti A, B e C delle equazioni dei due piani coincidono:

Considera le equazioni generali (o implicite) di due piani paralleli:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

La formula per calcolare la distanza tra due piani paralleli è:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

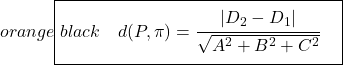
Quindi sicuramente è più semplice trovare la distanza tra due piani paralleli utilizzando la formula poiché si tratta solo di applicare la formula e basta, ma dipende dal problema. Inoltre, riteniamo che sia meglio spiegare entrambi i modi di calcolo della distanza in modo che tu possa scegliere quello che preferisci.

Esempio di calcolo della distanza tra due piani paralleli

Ad esempio, calcoleremo la distanza tra i seguenti due piani:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Dobbiamo innanzitutto verificare che abbiamo a che fare con due piani paralleli. Pertanto, tutti i coefficienti delle equazioni piane sono proporzionali tranne i termini indipendenti, quindi sono effettivamente due piani paralleli.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

In questo caso i termini A, B e C delle equazioni dei due piani non coincidono, ma possiamo ottenere questo risultato dividendo per due l’intera equazione del secondo piano:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Quindi le equazioni dei due piani hanno già gli stessi coefficienti A, B e C. Pertanto possiamo facilmente calcolare la distanza tra i due piani con la formula per la distanza tra due piani paralleli:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Sostituiamo i valori e risolviamo le operazioni:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Cosicché la distanza tra un piano e l’altro piano è uguale all’unità.

Risoluzione dei problemi di distanza da un punto ad un piano

Esercizio 1

Calcola la distanza tra il punto P e il piano la cui equazione cartesiana (o generale) è:

$P(2,0,-1) \qquad \qquad \pi: \ x-3y+2z-4=0$

vedi soluzione

Per calcolare la distanza dal punto al piano, è necessario utilizzare la formula corrispondente:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Sostituiamo il valore di ciascun parametro nella formula:

$d(P,\pi) = \cfrac{\lvert 1\cdot 2+(-3)\cdot 0+2\cdot (-1)-4\rvert}{\sqrt{1^2+(-3)^2+2^2}}$

E, infine, eseguiamo le operazioni:

$d(P,\pi) = \cfrac{\lvert 2+0-2-4\rvert}{\sqrt{1+9+4}}$

$d(P,\pi) = \cfrac{\lvert -4\rvert}{\sqrt{14}}$

$\bm{d(P,\pi) = }\cfrac{\bm{4}}{\bm{\sqrt{14}}}$

Esercizio 2

Trova la distanza tra il punto P e il piano π:

$P(-1,4,3) \qquad \qquad \pi: \ y=5x-2z$

vedi soluzione

Prima di utilizzare la formula per la distanza da un punto a un piano, dobbiamo prima esprimere il piano sotto forma di un’equazione implicita (o generale):

$\pi: \ -5x+y+2z=0$

E ora possiamo usare la formula per determinare la distanza dal punto al piano:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Sostituiamo il valore di ciascun termine nella formula:

$d(P,\pi) = \cfrac{\lvert -5\cdot (-1)+1\cdot 4+2\cdot 3+0\rvert}{\sqrt{(-5)^2+1^2+2^2}}$

E, infine, eseguiamo le operazioni:

$d(P,\pi) = \cfrac{\lvert 5+4+6\rvert}{\sqrt{25+1+4}}$

$\bm{d(P,\pi) = }\cfrac{\bm{15}}{\bm{\sqrt{30}}}$

Esercizio 3

Utilizza la formula per la distanza tra un punto e un piano per determinare se il punto P si trova nel piano π.

$P(0,-3,5) \qquad \qquad \pi: \ 4x+6y+2z+8=0$

vedi soluzione

Per verificare se il punto appartiene al piano possiamo calcolare la distanza tra i due: se la distanza è zero significa che il punto appartiene al piano, se invece la distanza è diversa da 0 significa che il punto appartiene al piano il punto è esterno al piano. piano.

Pertanto, determiniamo la distanza tra il punto e il piano dalla formula:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi) = \cfrac{\lvert 4\cdot 0+6\cdot (-3)+2\cdot 5+8\rvert}{\sqrt{4^2+6^2+2^2}}$

$d(P,\pi) = \cfrac{\lvert -18+10+8\rvert}{\sqrt{16+36+4}}$

$d(P,\pi) = \cfrac{0}{\sqrt{56}}$

$\bm{d(P,\pi) = 0}$

La distanza tra il punto e il piano è equivalente a zero, quindi effettivamente il punto appartiene al piano.

Esercizio 4

Trova la distanza tra i due piani seguenti:

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

vedi soluzione

Dobbiamo innanzitutto verificare che abbiamo a che fare con due piani paralleli. Tutti i coefficienti delle equazioni dei due piani sono proporzionali ad eccezione dei termini indipendenti, quindi si tratta effettivamente di due piani paralleli.

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

In questo caso calcoleremo la distanza tra i due piani con la formula, poiché i loro coefficienti A, B e C sono uguali:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Quindi, sostituiamo i valori nella formula ed eseguiamo le operazioni:

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

Esercizio 5

Trova la distanza tra i seguenti due piani paralleli:

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

vedi soluzione

Il piano in primo piano è definito sotto forma di equazioni parametriche, quindi per applicare la formula per la distanza tra due piani paralleli dobbiamo prima convertirla sotto forma di un’equazione generale e ci vogliono molti calcoli e tempo. Pertanto, è più veloce se prendiamo un punto su quel piano e calcoliamo la distanza da quel punto all’altro piano.

Pertanto, le coordinate di un punto attraverso il quale passa il piano π ₁ corrispondono ai termini indipendenti di ciascuna equazione parametrica:

$P(3,-2,5)$