Equazione implicita, generale o cartesiana del piano

Spiegazione di come viene calcolata l’equazione del piano implicita (formula), nota anche come equazione generale o cartesiana. Inoltre, troverai come trovare l’equazione del piano a partire dal suo vettore normale. E in più potrai vedere esempi ed esercizi risolti passo dopo passo.

Qual è l’equazione implicita o generale del piano?

Nella geometria analitica, l’ equazione implicita di un piano , chiamata anche equazione generale o cartesiana del piano, è un’equazione che consente di esprimere matematicamente qualsiasi piano. Per trovare l’equazione implicita o generale di un piano abbiamo bisogno di un punto e di due vettori linearmente indipendenti appartenenti a quel piano.

Formula dell’equazione implicita o generale del piano

Consideriamo un punto e due vettori di direzione di un piano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

L’equazione implicita, generale o cartesiana di un piano si ottiene risolvendo il seguente determinante e ponendo il risultato uguale a 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Pertanto, l’ equazione implicita o generale del piano risultante sarà la seguente:

$Ax+By+Cz+D=0$

È importante che i due vettori nella formula siano linearmente indipendenti l’uno dall’altro, ovvero debbano avere direzioni diverse. E perché questa condizione sia soddisfatta è sufficiente che i due vettori non siano paralleli.

Equazione implicita o generale o cartesiana di pan xy in r3

Sebbene non sia necessario conoscere il motivo di questa formula, puoi vederne la dimostrazione di seguito.

Partendo dalle equazioni parametriche di un piano passeremo all’equazione implicita (o generale) del piano:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Innanzitutto, passiamo il termine indipendente da ciascuna equazione parametrica all’altro lato dell’equazione:

$\displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

O equivalente:

$\displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}$

Affinché il sistema di equazioni sopra riportato abbia una soluzione ammissibile, il rango della seguente matrice deve essere uguale a 2 (teorema di Rouche-Frobenius):

$\displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}$

Quindi se l’intervallo della matrice precedente deve essere due, il determinante 3×3 dovrà necessariamente essere uguale a zero:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

E risolvendo questo determinante, otteniamo l’equazione generale, implicita o cartesiana di un piano:

$Ax+By+Cz+D=0$

Quindi, abbiamo appena visto l’equazione implicita (o generale) e le equazioni parametriche del piano, tuttavia ci sono ancora più modi per esprimere analiticamente un piano, come l’equazione vettoriale e l’equazione canonica. Puoi vedere la formula e la spiegazione di tutte le equazioni nel piano in questo link.

Esempio di come trovare l’equazione implicita o generale del piano

Vediamo come determinare l’equazione implicita (o generale o cartesiana) di un piano attraverso un esempio:

Trova l’equazione implicita o generale del piano che passa per il punto
$P(3,1,-1)$

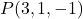
e contiene i vettori

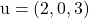
$\vv{\text{u}}=(2,0,3)$

E

$\vv{\text{v}}=(4,-1,2).$

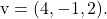
Per calcolare l’equazione generale o implicita del piano è necessario risolvere il seguente determinante formato dai due vettori, dalle variabili e dalle coordinate del punto:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Quindi sostituiamo i vettori e il punto nella formula:

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0$

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0$

E ora risolviamo il determinante di ordine 3, ad esempio con la regola di Sarrus o per cofattori (o deputati):

$-2(z+1)+12(y-1)+3(x-3)-4(y-1) = 0$

Ora operiamo e raggruppiamo i termini:

$3(x-3)+8(y-1) -2(z+1) = 0$

$3x-9+8y-8 -2z-2 = 0$

$3x+8y-2z-19 = 0$

Pertanto l’equazione implicita o generale del piano è:

$\bm{3x+8y-2z-19 = 0}$

Calcolare l’equazione implicita o generale di un piano a partire dal suo vettore normale

Un problema molto tipico nelle equazioni di un piano è trovare l’aspetto dell’equazione di un dato piano dato un punto e il suo vettore normale (o perpendicolare). Quindi, vediamo come funziona.

Ma devi prima sapere che le componenti X, Y, Z del vettore normale ad un piano coincidono rispettivamente con i coefficienti A, B, C dell’equazione implicita (o generale) di detto piano.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Oro

$\vv{n}$

è il vettore ortogonale al piano

$\pi.$

Una volta conosciuta la relazione precedente, vediamo un esempio di risoluzione di questo tipo di problemi di equazioni piane:

Determina l’equazione implicita o generale del piano che passa per il punto
$P(1,0,-2)$

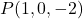
e uno dei suoi vettori normali lo è

$\vv{n}=(3,-1,2) .$

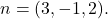
La formula per l’equazione implicita, generale o cartesiana di un piano è:

$Ax+By+Cz+D=0$

Quindi dal vettore normale possiamo ricavare i coefficienti A, B e C perché sono equivalenti alle componenti del suo vettore normale:

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

Mentre dobbiamo solo trovare il parametro D. Per fare ciò, sostituiamo nell’equazione le coordinate del punto che appartiene al piano:

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

Quindi l’equazione implicita o generale del piano è:

$\bm{3x-y+2z+1 = 0}$

Problemi risolti dell’equazione implicita o generale del piano

Esercizio 1

Trova l’equazione implicita o generale del piano che passa per il punto

$P(-2,1,3)$

e contiene i vettori

$\vv{\text{u}}=(4,1,3)$

$\vv{\text{v}}=(5,3,-1).$

vedi soluzione

Per calcolare l’equazione generale o implicita del piano è necessario risolvere il seguente determinante formato dai due vettori, dalle tre variabili e dalle coordinate del punto:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Quindi sostituiamo i vettori e il punto nella formula:

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

E ora risolviamo il determinante della matrice 3×3 con il metodo che preferisci:

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

Infine, eseguiamo le operazioni e raggruppiamo termini simili:

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

Quindi l’equazione implicita o generale del piano è:

$\bm{-8x+11y+7z-20 = 0}$

Esercizio 2

Determinare se il punto

$P(-1,5,-3)$

appartiene al seguente piano:

$\pi : \ 2x+y+6z-5=0$

vedi soluzione

Affinché il punto sia nel piano, è necessario verificarne l’equazione. Dobbiamo quindi sostituire le coordinate cartesiane del punto nell’equazione del piano e verificare se l’equazione è soddisfatta:

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

Il punto non rispetta l’equazione del piano, quindi non fa parte di questo piano.

Esercizio 3

Trova l’equazione implicita (o generale) del piano che contiene i seguenti tre punti:

$A(5,-1,-2) \qquad B(2,1,3) \qquad C(4,1,-2)$

vedi soluzione

Per trovare l’equazione implicita del piano, dobbiamo trovare due vettori linearmente indipendenti che si legano nel piano. E, per questo, possiamo calcolare due vettori definiti dai 3 punti:

$\vv{AB} = B - A = (2,1,3) - (5,-1,-2) = (-3,2,5)$

$\vv{AC} = C - A = (4,1,-2) - (5,-1,-2) = (-1,2,0)$

Le coordinate dei due vettori trovati non sono proporzionali, quindi sono effettivamente linearmente indipendenti l’uno dall’altro.

Ora conosciamo già due vettori di direzione e un punto del piano, quindi possiamo già applicare la formula per l’equazione generale del piano:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Sostituiamo i vettori e uno dei tre punti nella formula:

$\displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0$