Equazioni parametriche del piano

In questa pagina troverai cosa sono le equazioni parametriche di un piano e come si calcolano (formula). Inoltre, potrai vedere esempi ed esercitarti con esercizi risolti passo dopo passo.

Quali sono le equazioni parametriche di un piano?

Nella geometria analitica, le equazioni parametriche di un piano sono equazioni che consentono di esprimere matematicamente qualsiasi piano. Per trovare le equazioni parametriche di un piano abbiamo solo bisogno di un punto e di due vettori linearmente indipendenti appartenenti a quel piano.

Formulazione delle equazioni parametriche del piano

Consideriamo un punto e due vettori di direzione di un piano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

La formula per le equazioni parametriche di un piano è:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Oro

$\lambda$

$\mu$

sono due scalari, cioè due numeri reali.

È importante che i due vettori di direzione dell’equazione del piano siano linearmente indipendenti, cioè abbiano una direzione diversa (non parallela). Altrimenti, l’equazione di cui sopra non rappresenterebbe alcun piano.

D’altra parte, tieni presente che oltre all’equazione parametrica, ci sono altri modi per esprimere analiticamente un piano nello spazio (in R3), come l’ equazione generale del piano . In questo link troverai la sua formula, come si calcola dalle equazioni parametriche del piano, esempi ed esercizi risolti.

Esempio di come trovare le equazioni parametriche di un piano

Una volta visto qual è l’equazione parametrica del piano, vediamo come si calcola utilizzando un esempio:

Trovare le equazioni parametriche del piano passante per il punto
$P(1,3,2)$

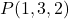
e contiene i vettori

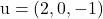
$\vv{\text{u}}=(2,0,-1)$

E

$\vv{\text{v}}=(4,2,3)$

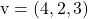
Per determinare le equazioni parametriche del piano è sufficiente applicare la sua formula:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

E ora sostituiamo il punto e ciascun vettore di direzione nell’equazione:

$\displaystyle \begin{cases}x=1 + \lambda \cdot 2 + \mu \cdot 4 \\[1.7ex] y=3+ \lambda \cdot 0 + \mu \cdot 2\\[1.7ex] z=2 + \lambda\cdot (-1)+ \mu \cdot 3\end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + 2\lambda + 4\mu } \\[1.7ex] \bm{y=3 + 2\mu}\\[1.7ex] \bm{z=2 -\lambda+ 3\mu} \end{cases}$

Come passare dall’equazione vettoriale di un piano alle equazioni parametriche

Un altro metodo per determinare le equazioni parametriche di un piano proviene dall’equazione vettoriale di un piano. Qui sotto potete vedere la demo.

Sia l’equazione vettoriale di qualsiasi piano:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Operiamo e realizziamo prima i prodotti dei vettori per gli scalari:

$(x,y,z)=(P_x,P_y,P_z)+ (\lambda\text{u}_x,\lambda\text{u}_y,\lambda\text{u}_z) +(\mu\text{v}_x,\mu\text{v}_y,\mu\text{v}_z)$

Successivamente, aggiungiamo i componenti:

$(x,y,z)=(P_x+\lambda \text{u}_x + \mu \text{v}_x,P_y+\lambda \text{u}_y + \mu \text{v}_y,P_z+\lambda \text{u}_z + \mu \text{v}_z)$

E, infine, otteniamo l’equazione parametrica del piano assimilando separatamente le coordinate corrispondenti a ciascuna variabile:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Come puoi vedere nei due esempi sopra, trovare le equazioni parametriche di un piano è relativamente semplice. Tuttavia, i problemi possono diventare un po’ complicati, quindi di seguito sono riportati diversi esercizi risolti di diversa difficoltà in modo da poter esercitarsi.

Risolti problemi di equazioni parametriche del piano

Esercizio 1

Determinare le equazioni parametriche del piano che contiene il vettore

$\vv{\text{u}}=(2,1,5)$

e passa attraverso i seguenti due punti:

$A(3,2,-1)$

$B(-2,-1,1).$

vedi soluzione

Per conoscere l’equazione di un piano occorrono un punto e due vettori e in questo caso abbiamo un solo vettore, dobbiamo quindi trovare un altro vettore direttore del piano. Per fare ciò possiamo calcolare il vettore che definisce i due punti del piano:

$\vv{AB} = B - A = (-2,-1,1) - (3,2,-1) = (-5,-3,2)$

Ora che conosciamo già due vettori di direzione del piano e un punto, utilizziamo quindi la formula per le equazioni parametriche del piano:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

E sostituiamo nell’equazione i due vettori e uno dei due punti del piano:

$\displaystyle \begin{cases}x=3 + \lambda \cdot 2+ \mu \cdot (-5) \\[1.7ex] y=2 + \lambda \cdot 1 + \mu \cdot (-3) \\[1.7ex] z=(-1) + \lambda\cdot 5 + \mu \cdot 2 \end{cases}$

$\displaystyle \begin{cases}\bm{x=3 +2 \lambda-5\mu } \\[1.7ex] \bm{y=2 + \lambda-3 \mu } \\[1.7ex] \bm{z=-1 + 5\lambda + 2\mu } \end{cases}$

Esercizio 2

Trova le equazioni parametriche del piano che contiene i seguenti tre punti:

$A(4,1,0) \qquad B(2,-3,-1) \qquad C(1,5,3)$

vedi soluzione

Per trovare le equazioni parametriche del piano, dobbiamo trovare due vettori linearmente indipendenti che si collegano nel piano. E, per questo, possiamo calcolare due vettori definiti dai 3 punti:

$\vv{AB} = B - A = (2,-3,-1) - (4,1,0) = (-2,-4,-1)$

$\vv{AC} = C - A = (1,5,3) - (4,1,0) = (-3,4,3)$

Le coordinate dei due vettori trovati non sono proporzionali, quindi sono linearmente indipendenti tra loro.

Ora che conosciamo già due vettori di direzione e un punto sul piano, applichiamo la formula per l’equazione parametrica del piano:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

E sostituiamo nell’equazione i due vettori e uno dei tre punti del piano:

$\displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}$

$\displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}$

Esercizio 3

Calcolare le equazioni parametriche del piano definito dalla seguente equazione vettoriale:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

vedi soluzione

Per trasformare l’equazione vettoriale del piano in un’equazione parametrica, è necessario operare con le coordinate quindi risolvere ciascuna variabile separatamente:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

$(x,y,z)=(0,-1,5)+(6\lambda,\lambda,-2\lambda) + (\mu,-\mu,3\mu)$

$(x,y,z)=(6\lambda+\mu,-1+\lambda-\mu,5-2\lambda+3\mu)$

$\displaystyle \begin{cases}\bm{x=6\lambda+\mu } \\[1.7ex] \bm{y=-1+\lambda-\mu} \\[1.7ex] \bm{z=5-2\lambda+3\mu } \end{cases}$

Esercizio 4

Trova le equazioni parametriche del piano che contiene la retta

$r$

ed è parallelo a destra

$s.$

essendo le linee:

$\displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}$

vedi soluzione

Per trovare le equazioni parametriche del piano, dobbiamo conoscere due vettori di direzione e un punto sul piano. L’istruzione ci dice che contiene la riga

$r$

Pertanto, possiamo prendere il vettore direzione e un punto su questa linea per definire il piano. Inoltre l’affermazione ci dice che il piano è parallelo alla retta

$s,$

quindi possiamo anche usare il vettore direzione di questa linea per l’equazione del piano.

la destra

$r$

è espresso sotto forma di equazioni parametriche, quindi le componenti del suo vettore direzione sono i coefficienti dei termini del parametro

$t:$

$\vv{r} =(1,-3,2)$

E le coordinate cartesiane di un punto su questa stessa linea sono i termini indipendenti delle equazioni parametriche:

$P(1,2,4)$

D’altra parte, la linea retta

$s$

ha la forma di un’equazione continua, tale che le componenti del suo vettore di direzione sono i denominatori delle frazioni:

$\vv{s} =(2,2,-3)$

Pertanto le equazioni parametriche del piano sono:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

$\displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}$

Quali sono le equazioni parametriche di un piano?

Formulazione delle equazioni parametriche del piano

Esempio di come trovare le equazioni parametriche di un piano

Come passare dall’equazione vettoriale di un piano alle equazioni parametriche

Risolti problemi di equazioni parametriche del piano

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta