Punto di equazione – pendenza della retta

In questa pagina troverai la formula per l’equazione punto-pendenza della retta e, inoltre, i diversi modi esistenti per calcolarla. Inoltre, potrai vedere diversi esempi ed esercitarti con esercizi risolti passo dopo passo.

Formula per l’equazione punto-pendenza della retta

L’equazione punto-pendenza di una linea è un modo per esprimere matematicamente una linea. In particolare, per trovare l’equazione punto-pendenza di una linea sono necessarie solo la pendenza e le coordinate di un punto sulla linea.

La formula per l’equazione punto-pendenza della retta è la seguente:

$y-y_0=m(x-x_0)$

Oro

$m$

è la pendenza della retta e

$x_0, y_0$

sono le coordinate di un punto sulla retta

$P(x_0,y_0).$

Vediamo come viene calcolata l’equazione punto-pendenza della retta utilizzando un esempio:

Scrivi l’equazione punto-pendenza della retta passante per il punto
$P(2,-1)$

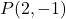
e pendenza m=3.

La formula per l’equazione punto-pendenza della retta è la seguente:

$y-y_0=m(x-x_0)$

In questo caso, l’affermazione ci dice che la pendenza della retta è m=3, quindi l’equazione della retta sarà la seguente:

$y-y_0=3(x-x_0)$

Inoltre sappiamo anche che la retta passa per il punto

$P(2,-1)$

, dobbiamo quindi sostituire le coordinate di questo punto nell’equazione:

$P(2,-1)$

$y-y_0=3(x-x_0) \ \xrightarrow{x_0=2 \ ; \ y_0=-1} \ y-(-1)=3(x-2)$

L’equazione punto-pendenza della retta è quindi:

$\bm{y+1=3(x-2)}$

Tieni presente che oltre all’equazione punto-pendenza, ci sono altri modi per esprimere analiticamente una linea: l’equazione vettoriale, le equazioni parametriche, l’equazione continua, l’equazione implicita (o generale) e l’equazione esplicita di una linea. Se sei più interessato, puoi controllare cosa è ciascuno di essi sul nostro sito web.

Cosa significa la pendenza di una retta?

Come abbiamo visto nella definizione dell’equazione punto-pendenza di una retta, il parametro

$m$

è la pendenza della retta. Ma in realtà… cosa significa la pendenza di una retta? Vediamolo dalla rappresentazione grafica di una linea:

Qual è l'equazione punto-pendenza di una retta?

La pendenza della linea indica la sua pendenza. Come puoi vedere dalla linea del grafico,

$m$

è uguale a 2 poiché la linea sale di 2 unità verticali per 1 unità orizzontale.

Ovviamente se la pendenza è positiva la funzione è crescente (sale), invece se la pendenza è negativa la funzione è decrescente (scende).

Come calcolare la pendenza di una retta

Inoltre, ci sono 3 modi diversi per determinare numericamente la pendenza di una linea:

Dati due punti diversi sulla retta
$P_1(x_1,y_1)$

E

$P_2(x_2,y_2),$

La pendenza della retta è pari a:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Sì
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

è il vettore direzione della retta, la sua pendenza è:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Sì
$\alpha$

è l’angolo formato dalla retta con l’asse delle ascisse (asse X), la pendenza della retta è equivalente alla tangente di detto angolo:

$m = \text{tg}(\alpha )$

formula per l'equazione esplicita della retta

Posizione relativa delle linee

Infine, la pendenza di una linea viene utilizzata anche per conoscere la relazione tra più linee. Poiché due rette parallele hanno la stessa pendenza e, d’altra parte, se la pendenza di una retta è l’inverso negativo della pendenza di un’altra retta, ciò significa che queste due rette sono perpendicolari .

Calcolare l’equazione punto-pendenza della retta che passa per due punti

Un problema molto comune è quello di determinare l’equazione punto-pendenza a partire da due punti appartenenti alla retta. Vediamo come si risolve attraverso un esempio:

Trova l’equazione punto-pendenza della retta che passa per i seguenti due punti:

$P_1(5,2) \qquad P_2(3,6)$

Per trovare l’equazione punto-pendenza della retta, dobbiamo determinare qual è la pendenza della retta. Quindi calcoliamo la pendenza della linea utilizzando la formula dei due punti:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{6-2}{3-5} = \cfrac{4}{-2}= -2$

Pertanto, l’equazione punto-pendenza della retta sarà la seguente:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Basta quindi sostituire nell’equazione le coordinate cartesiane di un punto sulla retta:

$P_1(5,2)$

$y-y_0=-2(x-x_0) \ \xrightarrow{x_0=5 \ ; \ y_0=2} \ y-2=-2(x-5)$

$\bm{y-2=-2(x-5)}$

Va bene anche se inseriamo l’altro punto dell’affermazione nell’equazione della retta:

$P_1(3,6)$

$y-6=-2(x-3)$

Trova l’equazione punto-pendenza di una linea dal grafico

Come abbiamo visto nelle sezioni precedenti, ci sono diversi modi per trovare numericamente l’equazione punto-pendenza di una linea. Tuttavia, può essere trovato anche graficamente. Vediamo come si realizza attraverso un esempio:

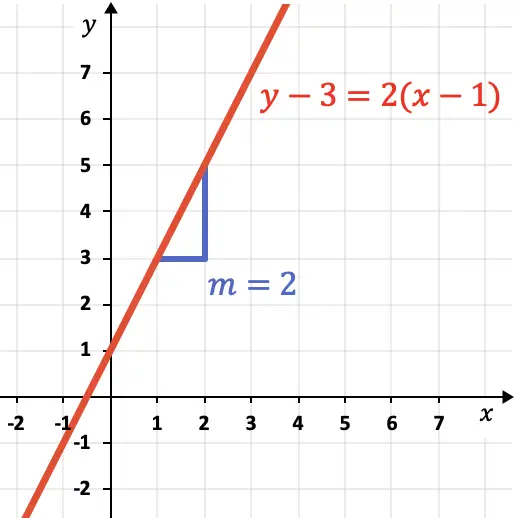
Determinare l’equazione punto-pendenza della linea mostrata nel grafico seguente:

Per determinare l’equazione punto-pendenza della linea tracciata, dobbiamo trovare la sua pendenza e un punto sulla linea.

In questo caso la pendenza della linea è pari a 3, perché la linea sale di 3 unità verticali per ogni unità orizzontale.

$m = 3$

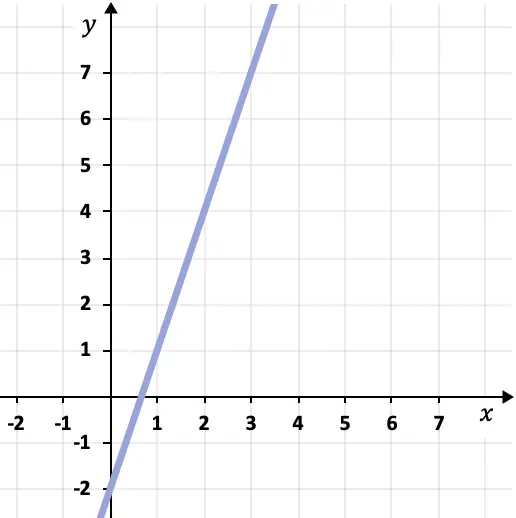
Successivamente abbiamo bisogno di un punto sulla linea. Per fare ciò possiamo scegliere un punto qualsiasi del grafico attraverso il quale passa la retta, ad esempio il punto (1,1).

$P(1,1)$

Pertanto, ora possiamo trovare l’equazione punto-pendenza della retta applicando la sua formula:

$y-y_0=m(x-x_0)$

$y-1=3(x-1)$

determinare graficamente la pendenza del punto di equazione di una retta

Risolti problemi di equazione punto-pendenza

Esercizio 1

Scrivi l’equazione punto-pendenza della retta passante per il punto

$P(1,4)$

e la sua pendenza è

$m=-2.$

vedi soluzione

La formula per l’equazione punto-pendenza della retta è:

$y-y_0=m(x-x_0)$

In questo caso, l’affermazione ci dice che la pendenza della retta è m=-2, quindi l’equazione della retta sarà la seguente:

$y-y_0=-2(x-x_0)$

Inoltre dall’affermazione sappiamo anche che la retta passa per il punto

$P(1,4)$

, è quindi sufficiente sostituire le coordinate del punto nell’equazione della retta:

$P(1,4)$

$\bm{y-4=-2(x-1)}$

Esercizio 2

Qual è l’equazione punto-pendenza della retta che passa per i seguenti due punti?

$P_1(1,6) \qquad P_2(4,0)$

vedi soluzione

Per trovare l’equazione punto-pendenza della retta, dobbiamo determinare qual è la pendenza della retta. Calcoliamo quindi la pendenza della retta con la sua formula:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{0-6}{4-1} = \cfrac{-6}{3}= -2$

Pertanto, l’equazione punto-pendenza della retta sarà la seguente:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Pertanto, dobbiamo solo sostituire le coordinate di un punto sulla retta nell’equazione:

$P_1(1,6)$

$\bm{y-6=-2(x-1)}$

Sarebbe stato corretto inserire nell’equazione anche l’altro punto dell’affermazione:

$y=-2(x-4)$

Esercizio 3

Trova l’equazione punto-pendenza della retta che passa per i seguenti due punti:

$P_1(1,-2) \qquad P_2(2,3)$

vedi soluzione

Per trovare l’equazione punto-pendenza della linea, devi prima calcolare la sua pendenza:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{3-(-2)}{2-1} = \cfrac{3+2}{1}=\cfrac{5}{1}= 5$

Pertanto, l’equazione punto-pendenza della retta sarà la seguente:

$y-y_0=m(x-x_0)$

$y-y_0=5(x-x_0)$

Pertanto, dobbiamo solo sostituire le coordinate di un punto sulla retta nell’equazione:

$P_1(1,-2)$

$y-(-2)=5(x-1)$

$\bm{y+2=5(x-1)}$

È anche corretto inserire l’altro punto dell’affermazione nell’equazione della retta:

$y-3=5(x-2)$

Esercizio 4

Calcola l’equazione punto-pendenza della linea che forma un angolo di 45º con l’asse X e passa per l’origine delle coordinate.

vedi soluzione

Se la retta forma un angolo di 45 gradi con l’asse OX, la sua pendenza sarà:

$m = \text{tg}(45º) = 1$

$y-y_0=1(x-x_0)$

$y-y_0=x-x_0$

E una volta che conosciamo la pendenza della retta, possiamo trovare l’equazione punto-pendenza sostituendo un punto sulla retta nell’equazione. Inoltre, l’affermazione ci dice che la linea passa attraverso l’origine delle coordinate, il che significa che passa attraverso il punto (0,0). Ancora:

$P(0,0)$