Limiti trigonometrici -

Qui scoprirai come risolvere i limiti trigonometrici. Potrai vedere diversi esempi di limiti delle funzioni trigonometriche e persino esercitarti con esercizi passo passo risolti sui limiti trigonometrici.

Cosa sono i limiti trigonometrici?

I limiti trigonometrici sono limiti calcolati su funzioni trigonometriche. Per risolvere i limiti trigonometrici occorre applicare una procedura preliminare, perché generalmente danno luogo a indeterminazioni.

Inoltre, non esistono limiti infiniti delle funzioni trigonometriche, perché sono funzioni periodiche. Cioè i suoi grafici si ripetono continuamente periodicamente senza tendere verso un valore specifico.

Formule limite trigonometriche

Tutti i limiti trigonometrici sono calcolati dalle seguenti due formule:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=1$

Dimostrazione della formula

Se proviamo a calcolare il limite per sostituzione, otteniamo l’indeterminazione zero tra zero:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=\frac{\text{sen}(0)}{0}=\frac{0}{0}$

Ma questa formula trigonometrica può essere dimostrata calcolando i valori della funzione più vicina e più vicina a x=0 (angoli in radianti).

$\displaystyle f(x)=\frac{\text{sen}(x)}{x}=1$

$\begin{array}{c}\begin{array}{l}f(-1)=\cfrac{\text{sen}(-1)}{-1}=0,84147\\[3ex]f(-0,1)=\cfrac{\text{sen}(-0,1)}{-0,1}=0,99833\\[3ex]f(-0,01)=\cfrac{\text{sen}(-0,01)}{-0,01}=0,99998\\[3ex]f(-0,001)=\cfrac{\text{sen}(-0,001)}{-0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=1\end{array}$

$\begin{array}{c}\begin{array}{l}f(1)=\cfrac{\text{sen}(1)}{1}=0,84147\\[3ex]f(0,1)=\cfrac{\text{sen}(0,1)}{0,1}=0,99833\\[3ex]f(0,01)=\cfrac{\text{sen}(0,01)}{0,01}=0,99998\\[3ex]f(0,001)=\cfrac{\text{sen}(0,001)}{0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\end{array}$

I due limiti laterali della funzione trigonometrica danno 1, quindi il limite nel punto x=0 è 1:

$\begin{array}{c}\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\\[3ex]\color{orange}\bm{\downarrow}\\[2ex]\lim_{x\to 0}\displaystyle\frac{\text{sen}(x)}{x}=1\end{array}$

Pertanto, il limite trigonometrico del seno di x diviso per x quando x tende a 0 è uguale a 1.

Questa formula può essere applicata anche per più angoli:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(kx)}{kx}=1$

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=0$

Dimostrazione della formula

Se proviamo a trovare il limite per sostituzione diretta, otteniamo la forma indeterminata zero tra zero:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=}\frac{1-\text{cos}(0)}{0}=\frac{1-1}{0}=\frac{0}{0}$

Ma possiamo verificare l’uguaglianza dalla formula sopra. Per fare ciò, devi prima moltiplicare il numeratore e il denominatore della frazione per 1 più il coseno di x:

$\displaystyle\lim_{x\to 0}\frac{\bigl(1-\text{cos}(x)\bigr)\cdot \bigl(1+\text{cos}(x)\bigr)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

Ora abbiamo un’identità notevole nel numeratore della frazione, quindi possiamo semplificarla:

$\displaystyle\lim_{x\to 0}\frac{1^2-\text{cos}^2(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}^2(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

Partendo dall’identità trigonometrica fondamentale, riscriviamo il numeratore:

$\text{sen}^2(x)+\text{cos}^2(x)=1 \ \longrightarrow \ \text{sen}^2(x)=1-\text{cos}^2(x)$

$\displaystyle\lim_{x\to 0}\frac{\text{sen}^2(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

Possiamo quindi trasformare la frazione in un prodotto di frazioni:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)\cdot \text{sen}(x)}{x\cdot \bigl(1+\text{cos}(x)\bigr)}$

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{\text{sen}(x)}{1+\text{cos}(x)}$

Utilizzando le proprietà dei limiti, possiamo convertire l’espressione sopra in un prodotto di limiti:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \lim_{x\to 0}\frac{\text{sen}(x)}{1+\text{cos}(x)}$

Utilizzando la formula dimostrata sopra, possiamo facilmente semplificare il limite trigonometrico:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=1$

$\displaystyle 1\cdot \lim_{x\to 0}\frac{\text{sen}(x)}{1+\text{cos}(x)}$

$\displaystyle \lim_{x\to 0}\frac{\text{sen}(x)}{1+\text{cos}(x)}$

E infine, calcoliamo il limite risultante:

$\displaystyle \lim_{x\to 0}\frac{\text{sen}(0)}{1+\text{cos}(0)}=\frac{0}{1+1}=\frac{0}{2}=0$

Pertanto, la formula del limite trigonometrico è verificata:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=0$

Come l’altra formula, può essere utilizzata anche per più angoli:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(kx)}{kx}=0$

Pertanto, per risolvere i limiti trigonometrici, dobbiamo usare l’aritmetica per trasformare le funzioni e ottenere espressioni simili a queste. In questo modo possiamo utilizzare una delle due formule e trovare il valore del limite.

D’altra parte, a volte potremmo aver bisogno di applicare alcune identità trigonometriche, quindi lasciamo a te tutte le formule seguenti

Identità trigonometriche

Formula che collega i tre principali rapporti trigonometrici:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

Identità trigonometrica fondamentale:

$\text{sen}^2(x)+\text{cos}^2(x)=1$

Relazioni trigonometriche derivate dalla fondamentale:

$1+\text{tan}^2 (x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)$

$1+\text{cot}^2 (x)=\cfrac{1}{\text{sen}2(x)}=\text{cosec}^2(x)$

Angoli opposti:

$\text{sen}(-x)=-\text{sen}(x)$

$\text{cos}(-x)=\text{cos}(x)$

$\text{tan}(-x)=-\text{tan}(x)$

Somma di due angoli:

$\text{sen}(x+y)=\text{sen}(x)\text{cos}(y)+\text{cos}(x)\text{sen}(y)$

$\text{cos}(x+y)=\text{cos}(x)\text{cos}(y)-\text{sen}(x)\text{sen}(y)$

$\text{tan}(x+y)=\cfrac{\text{tan}(x)+\text{tan}(y)}{1-\text{tan}(x)\text{tan}(y)}$

Differenza di due angoli:

$\text{sen}(x-y) = \text{sen}(x)\text{cos}(y)-\text{cos}(x)\text{sen}(y)$

$\text{cos}(x-y) = \text{cos}(x)\text{cos}(y)+ \text{sen}(x) sen(y)$

$\text{tan}(x-y)=\cfrac{\text{tan}(x)-\text{tan}(y)}{1+\text{tan}(x)\text{tan}(y)}$

Doppio angolo:

$\text{sen}(2x) = 2\text{sen}(x)\text{cos}(x)$

$\text{cos}(2x) =\text{cos}^2(x)-\text{sen}^2(x)$

$\text{tan}(2x) =\cfrac{2\text{tan}(x)}{1-\text{tan}^2(x)}$

Mezzo angolo:

$\displaystyle \text{sen}\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1-\text{cos}(x)}{2}}$

$\displaystyle \text{cos}\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1+\text{cos}(x)}{2}}$

$\displaystyle\text{tan}\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1-\text{cos}(x)}{1+\text{cos}(x)}}$

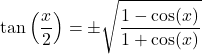
Addizione e sottrazione di seno e coseno:

$\displaystyle \text{sen}(x)+\text{sen}(y)=2\text{sen}\left(\frac{x+y}{2} \right)\text{cos}\left(\frac{x-y}{2} \right)$

$\displaystyle \text{sen}(x)-\text{sen}(y)=2\text{cos}\left(\frac{x+y}{2} \right)\text{sen}\left(\frac{x-y}{2} \right)$

$\displaystyle \text{cos}(x)+\text{cos}(y)=2\text{cos}\left(\frac{x+y}{2} \right)\text{cos}\left(\frac{x-y}{2} \right)$

$\displaystyle \text{cos}(x)-\text{cos}(y)=-2\text{sen}\left(\frac{x+y}{2} \right)\text{sen}\left(\frac{x-y}{2} \right)$

Prodotto di seni e coseni:

$\displaystyle \text{sen}(x)\cdot \text{sen}(y)=\frac{1}{2}\Bigl[\text{cos}(x-y)-\text{cos}(x+y)\Bigr]$

$\displaystyle \text{cos}(x)\cdot \text{cos}(y)=\frac{1}{2}\Bigl[\text{cos}(x+y)+\text{cos}(x-y)\Bigr]$

$\displaystyle \text{sen}(x)\cdot \text{cos}(y)=\frac{1}{2}\Bigl[\text{sen}(x+y)+\text{sen}(x-y)\Bigr]$

Affinché tu possa vedere esattamente come vengono calcolati i limiti trigonometrici, abbiamo messo insieme un esempio passo passo di seguito.

Esempio di limite trigonometrico

Vediamo come viene risolto un limite trigonometrico utilizzando il seguente esempio:

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)}{x}$

Provando a calcolare il limite trigonometrico otteniamo l’indeterminatezza dello zero tra zero:

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)}{x}=\frac{\text{tan}(0)}{0}=\frac{0}{0}$

➤ Vedi: zero limiti tra zero

È quindi necessario trasformare la funzione trigonometrica per risolvere il limite. La funzione tangente è uguale al seno diviso coseno, quindi:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)}{x}=\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{x}$

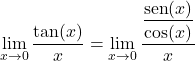
Possiamo ora esprimere la funzione come prodotto applicando le proprietà delle frazioni:

$\displaystyle\frac{\displaystyle\frac{a}{b}}{\displaystyle\frac{c}{d}}=\frac{a\cdot d}{b\cdot c}$

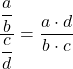
$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{\displaystyle\frac{x}{1}}=\lim_{x\to 0}{\frac{\text{sen}(x)\cdot 1}{\text{cos}(x) \cdot x}=\\[6ex]\displaystyle =\lim_{x\to 0}{\frac{\text{sen}(x)}{x\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{1}{\text{cos}(x)}\end{array}$

Utilizzando le proprietà dei limiti, possiamo convertire il limite di due funzioni moltiplicate nel prodotto di due limiti:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\frac{1}{\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{1}{\text{cos}(x)}$

Come abbiamo mostrato sopra, il primo limite trigonometrico dà 1:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}=1$

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{1}{\text{cos}(x)}=1\cdot\lim_{x\to 0}\frac{1}{\text{cos}(x)}=\lim_{x\to 0}\frac{1}{\text{cos}(x)}$

Quindi basta fare il seguente calcolo:

$\displaystyle \lim_{x\to 0}\frac{1}{\text{cos}(x)}=\frac{1}{\text{cos}(0)}=\frac{1}{1}=1$

Esercizi risolti sui limiti trigonometrici

Esercizio 1

Risolvi il seguente limite trigonometrico:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(4x)}{2x}$

Vedi la soluzione

Per prima cosa proviamo a calcolare il limite trigonometrico mediante valutazione diretta:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(4x)}{2x}=\frac{\text{sen}(4\cdot 0)}{2\cdot 0}=\frac{0}{0}$

Ma otteniamo zero su zero indeterminatezza. Quindi dobbiamo applicare le trasformazioni alla funzione.

Innanzitutto, lasceremo semplicemente la x al denominatore procedendo come segue:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(4x)}{2x}=\lim_{x\to 0}\frac{1}{2}\cdot\frac{\text{sen}(4x)}{x}=\frac{1}{2}\cdot\lim_{x\to 0}\frac{\text{sen}(4x)}{x}$

Ora moltiplichiamo e dividiamo la frazione per 4 per ottenere un’espressione con cui si può applicare la prima formula per i limiti trigonometrici:

$\displaystyle\frac{1}{2}\lim_{x\to 0}\frac{\text{sen}(4x)\cdot 4}{x\cdot 4}=\frac{1}{2}\cdot 4 \cdot \lim_{x\to 0}\frac{\text{sen}(4x)}{4x}=2\lim_{x\to 0}\frac{\text{sen}(4x)}{4x}$

Infine applichiamo la formula vista all’inizio e risolviamo il limite trigonometrico:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(kx)}{kx}=1$

$\displaystyle 2\lim_{x\to 0}\frac{\text{sen}(4x)}{4x}=2\cdot 1=\bm{2}$

Esercizio 2

Calcolare il seguente limite trigonometrico:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)+\text{tan}(x)}{x}$

Vedi la soluzione

Per prima cosa proviamo a trovare il limite trigonometrico:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)+\text{tan}(x)}{x}=\frac{\text{sen}(0)+\text{tan}(0)}{0}=\frac{0}{0}$

Ma la forma indeterminata dello zero corrisponde allo zero raggiunto.

Quindi, convertiamo la tangente in un quoziente tra seno e coseno:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)+\text{tan}(x)}{x}=\lim_{x\to 0}\frac{\displaystyle\text{sen}(x)+\frac{\text{sen}(x)}{\text{cos}(x)}}{x}$

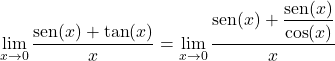
Moltiplichiamo e dividiamo per il coseno di x:

$\displaystyle\lim_{x\to 0}\frac{\left(\displaystyle\text{sen}(x)+\frac{\text{sen}(x)}{\text{cos}(x)}\right)\cdot\text{cos}(x)}{x\cdot\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)\text{cos}(x)+\text{sen}(x)}{x\cdot\text{cos}(x)}$

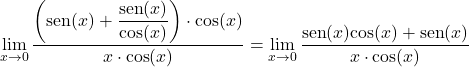
Prendiamo un fattore comune al numeratore e separiamo il limite trigonometrico in due:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)(\text{cos}(x)+1)}{x\cdot\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{\text{cos}(x)+1}{\text{cos}(x)}$

E infine, troviamo il risultato del limite trigonometrico:

$\displaystyle\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot\lim_{x\to 0}\frac{\text{cos}(x)+1}{\text{cos}(x)}=1\cdot\frac{\text{cos}(0)+1}{\text{cos}(0)} =\frac{1+1}{1}=\bm{2}$

Esercizio 3

Risolvi il limite della seguente funzione trigonometrica quando x tende a zero:

$\displaystyle\lim_{x\to 0}\frac{\text{tan}(x)-\text{sen}{(x)}}{3x\cdot\text{tan}(x)}$

Vedi la soluzione

Facendo il calcolo diretto otteniamo il limite indeterminato 0 tra 0:

$\displaystyle\lim_{x\to 0}}\frac{\text{tan}(x)-\text{sen}(x)}{3x\cdot\text{tan}(x)}=\frac{\text{tan}(0)-\text{sen}(0)}{3\cdot 0\cdot\text{tan}(0)}=\frac{0}{0}$

Pertanto, semplificheremo il limite dividendo ciascun termine per la tangente di x:

$\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{tan}(x)}{\text{tan}(x)}-\frac{\text{sen}(x)}{\text{tan}(x)}}{\displaystyle\frac{3x\cdot\text{tan}(x)}{\text{tan}(x)}}=\lim_{x\to 0}\frac{\displaystyle 1-\frac{\text{sen}(x)}{\text{tan}(x)}}{3x}$

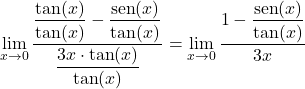
In secondo luogo, possiamo dedurre dall’identità trigonometrica fondamentale che la frazione del numeratore è equivalente al coseno di x:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}\ \longrightarrow \ \text{cos}(x)=\cfrac{\text{sen}(x)}{\text{tan}(x)}$

$\displaystyle\lim_{x\to 0}\frac{\displaystyle 1-\frac{\text{sen}(x)}{\text{tan}(x)}}{3x}=\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}$

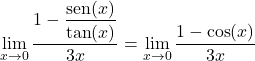
E applicando la seconda formula dimostrata nella teoria dei limiti trigonometrici, possiamo facilmente risolvere il limite:

$\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=0$

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}=\lim_{x\to 0}\frac{1}{3}\cdot \frac{1-\text{cos}(x)}{x}=\\[4ex]\displaystyle =\frac{1}{3}\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=\frac{1}{3}\cdot 0=\bm{0}\end{array}$

Esercizio 4

Determina la soluzione del seguente limite trigonometrico nel punto x=0:

$\displaystyle\lim_{x\to 0}\frac{2\text{sen}(x)\text{cos}(x)\text{sen}(5x)}{x^2}$

Vedi la soluzione

Se proviamo a risolvere il limite, troviamo la forma indeterminata 0/0:

$\displaystyle\lim_{x\to 0}\frac{2\text{sen}(x)\text{cos}(x)\text{sen}(5x)}{x^2}=\frac{2\text{sen}(0)\text{cos}(0)\text{sen}(5\cdot 0)}{0^2}=\frac{0}{0}$

L’espressione algebrica del numeratore può essere riscritta utilizzando l’identità trigonometrica del seno di un doppio angolo:

$\text{sen}(2x)=2\text{sen}(x)\text{cos}(x)$

$\displaystyle\lim_{x\to 0}\frac{2\text{sen}(x)\text{cos}(x)\text{sen}(5x)}{x^2}=\lim_{x\to 0}\frac{\text{sen}(2x)\text{sen}(5x)}{x^2}$

Ora separiamo il limite della funzione trigonometrica in un prodotto:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)\cdot \text{sen}(5x)}{x\cdot x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}\end{array}$

E, infine, risolviamo il limite trigonometrico applicando le proprietà dei limiti:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =2\cdot \lim_{x\to 0}\frac{\text{sen}(2x)}{2x}\cdot 5\cdot \lim_{x\to 0}\frac{\text{sen}(5x)}{5x}=\\[4ex]\displaystyle =2\cdot 1\cdot 5\cdot 1=\bm{10}\end{array}$

Cosa sono i limiti trigonometrici?

Formule limite trigonometriche

Esempio di limite trigonometrico

Esercizi risolti sui limiti trigonometrici

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta