In questa pagina spieghiamo cos’è un sistema di coordinate e, inoltre, troverai tutto sul sistema di coordinate cartesiane. Vedrai anche altri tipi di sistemi di coordinate (polari, cilindrici, sferici, ecc.) e applicazioni reali di un sistema di coordinate.
Cos’è un sistema di coordinate?
Sebbene all’inizio sia un po’ difficile comprendere questo concetto, la definizione di sistema di coordinate è:
Un sistema di coordinate è un sistema che ci permette di identificare la posizione di un punto. Cioè, è un insieme di valori utilizzati per definire la posizione di qualsiasi oggetto geometrico.
Ad esempio, la posizione in cui vola l’aereo che segue può essere descritta da un sistema di coordinate:
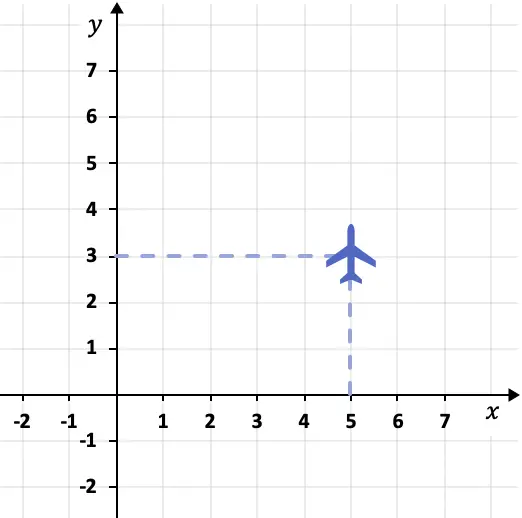
In questo caso l’aereo è nel punto (5.3). Perché la sua coordinata X è 5 e la sua coordinata Y è 3.
![]()
D’altra parte, il punto (0,0) è chiamato origine delle coordinate , perché è dove iniziano gli assi delle coordinate ed è il punto di riferimento del sistema di coordinate.
Per curiosità, si ritiene che il matematico che ha inventato il sistema di coordinate sia stato il francese René Descartes. Ed è per questo che è chiamato anche sistema di coordinate cartesiane.
Sistema di coordinate cartesiane nel piano
Il grafico che abbiamo visto nella sezione precedente appartiene al sistema di coordinate cartesiane nel piano. Diciamo che è nel piano perché è un sistema bidimensionale, vale a dire che ha solo due assi: l’asse X e l’asse Y.
L’asse X corrisponde alle coordinate orizzontali, mentre l’asse Y rappresenta le coordinate verticali. Di seguito potete vedere diversi punti rappresentati graficamente con le relative coordinate:
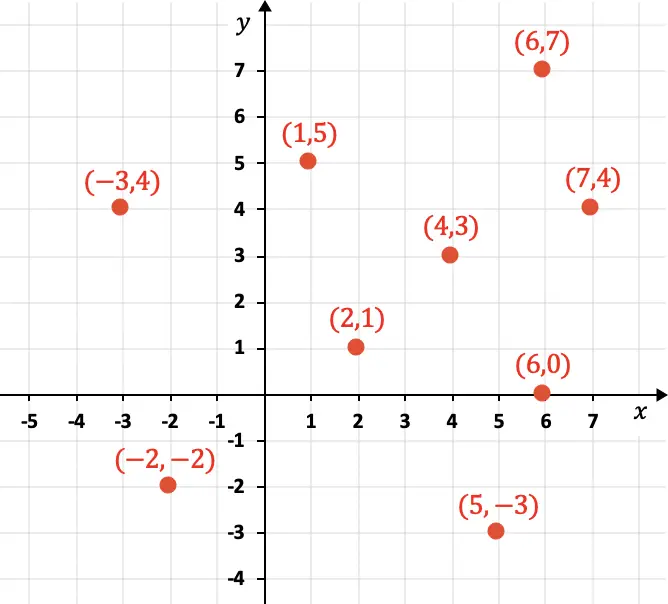
Come puoi vedere nel grafico, le coordinate sono rappresentate numericamente tra parentesi, inoltre viene messa prima la componente X e poi la componente Y: (4,3). Inoltre, le coordinate possono essere positive, negative o zero.
D’altra parte, questo tipo di sistema di coordinate è anche chiamato piano cartesiano.
Infine, dovresti sapere che gli assi coordinati possono essere detti in diversi modi, sebbene significhino tutti la stessa cosa:
- L’asse X è anche chiamato asse delle ascisse o asse OX.
- L’asse Y è anche chiamato asse y o asse OY.
Sistema di coordinate cartesiane nello spazio
Abbiamo appena visto come rappresentare un punto nel piano, cioè in un sistema di coordinate a due assi (2 dimensioni). Tuttavia, la realtà è composta da 3 dimensioni (altezza, larghezza e profondità).
Pertanto, nella geometria euclidea, lo spazio tridimensionale è generalmente rappresentato da un sistema di coordinate con tre assi, tutti perpendicolari tra loro:
- L’asse X rappresenta la profondità.
- L’asse Y indica la larghezza.
- L’asse Z corrisponde all’altezza.
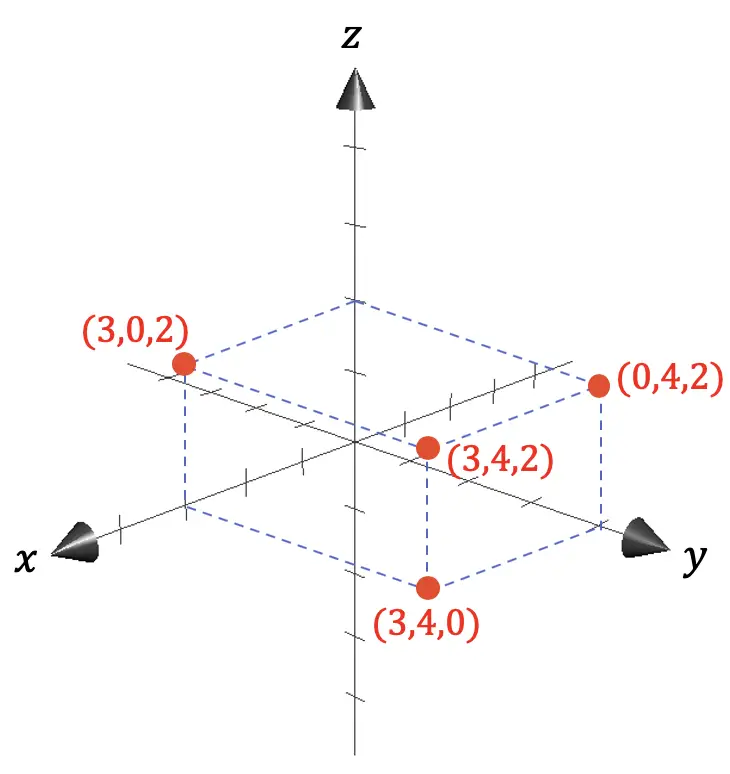
Come puoi vedere nella rappresentazione grafica precedente, le coordinate di un qualsiasi punto sono date dalle proiezioni sugli assi delle distanze tra il punto in questione e l’origine (0,0,0).
sistema di coordinate polari
I sistemi di coordinate cartesiane, 2D o 3D, sono i più utilizzati. Ma in alcune occasioni potrebbe essere conveniente per noi utilizzare un altro tipo di sistema di coordinate.
Il sistema di coordinate polari è un sistema di riferimento bidimensionale le cui coordinate sono:
-

è la distanza tra l’origine delle coordinate e il punto. Questa è chiamata coordinata radiale.
-

è l’angolo che forma l’asse X con la retta passante per il punto e l’origine. Questa è chiamata coordinata angolare o azimutale.
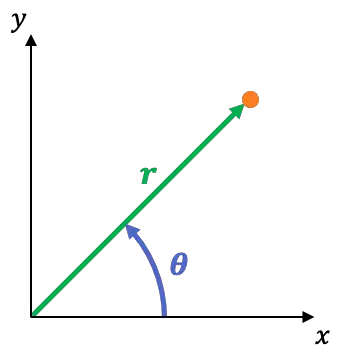
Puoi passare facilmente dal sistema di coordinate rettangolari al sistema di coordinate polari utilizzando le seguenti equazioni:
Convertire le coordinate polari in coordinate cartesiane
![]()
![]()
Passaggio dalle coordinate cartesiane alle coordinate polari
![]()
![]()
Sistema di coordinate cilindriche
Il sistema di coordinate cilindriche è molto simile al sistema di coordinate polari. In effetti è la stessa cosa ma con una coordinata in più: l’altezza.
La cornice cilindrica è quindi una cornice tridimensionale, vale a dire con 3 coordinate:
-

è la proiezione ortogonale del punto nel piano XY, o in altre parole, la distanza del punto dall’asse Z.
-

è l’angolo formato dal semiasse positivo

-

è l’altezza del punto, è la stessa coordinata del sistema di coordinate cartesiane nello spazio.
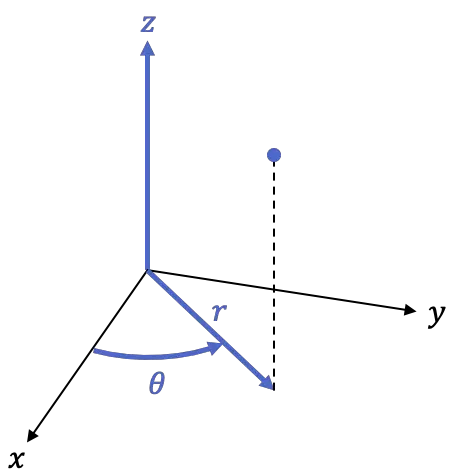
Le seguenti formule vengono utilizzate per trasformare il sistema di coordinate cartesiane in coordinate cilindriche:
Convertire le coordinate cilindriche in coordinate cartesiane
![]()
![]()
![]()
Convertire le coordinate cartesiane in coordinate cilindriche
![]()
![]()
![]()
Sistema di coordinate sferiche
Infine abbiamo il sistema di coordinate sferiche. Anche questo tipo di sistema di coordinate è abbastanza simile alle coordinate polari e alle coordinate cilindriche, anche se ovviamente presenta alcune differenze da esse.
Il sistema di coordinate sferiche è un sistema per descrivere spazi euclidei tridimensionali, pertanto ha tre coordinate:
-

è la distanza (in R3) dall’origine al punto.
-

è l’angolo che la parte positiva dell’asse X forma con la linea

proiettato sul piano XY.
-
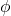
è l’angolo tra la parte positiva dell’asse Z e la linea

Puoi passare dalle coordinate sferiche a quelle cartesiane utilizzando le seguenti formule:
Conversione di coordinate sferiche in coordinate cartesiane
![]()
![]()
![]()
Conversione delle coordinate cartesiane in coordinate sferiche
![]()
![]()
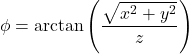
Applicazioni reali del sistema di coordinate
I sistemi di coordinate sono così importanti in matematica perché vengono utilizzati anche nella vita reale. Ad esempio, sono utili per localizzare oggetti, persone o anche luoghi su una mappa. In effetti, il GPS esiste grazie ai sistemi di coordinate, poiché è ciò che usano per conoscere la tua posizione sulla Terra.
Più precisamente, le coordinate geografiche GPS sono composte da due elementi: latitudine e longitudine. La latitudine (nord o sud) e la longitudine (est o ovest) sono due coordinate angolari che misurano l’angolo tra il centro della Terra e la tua posizione. Entrambi sono espressi in gradi, sia in coordinate decimali che sessagesimali.