▷ Come trovare la funzione inversa o reciproca (esercizi risolti)

In questo articolo spieghiamo cos’è una funzione inversa (o reciproca) e come calcolare l’inversa di una funzione. Scoprirai anche come sapere facilmente se una funzione ha un inverso o meno e le proprietà di questo tipo di funzioni. Infine, puoi esercitarti con esercizi passo passo sulle funzioni inverse.

Qual è la funzione inversa?

La funzione inversa, detta anche funzione reciproca, è la funzione il cui dominio è l’intervallo di un’altra funzione (la funzione originaria) e il cui intervallo è il dominio della funzione originaria. La funzione inversa della funzione f si esprime con il simbolo f ^-1 .

Pertanto, la funzione inversa di f(x) è la funzione che soddisfa la seguente condizione:

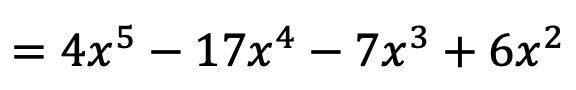
Oro

$f^{-1}$

è la funzione inversa di

$f.$

Il concetto di funzione inversa può essere definito anche utilizzando la composizione di funzioni, poiché qualsiasi funzione composta con la sua funzione inversa è uguale alla funzione identità:

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

➤ Vedi: cos’è la composizione della funzione?

Quindi se l’equazione precedente è soddisfatta, significa che

$f^{-1}$

è la funzione inversa (o funzione reciproca) di

$f.$

Esempio di funzione inversa

Data la definizione di funzione inversa, risolviamo un esempio per comprenderne meglio il significato.

Determina se le seguenti funzioni sono tra loro inverse:

$f(x)=2x+1\qquad g(x)=\cfrac{x-1}{2}$

Se le due funzioni sono tra loro inverse, saranno soddisfatte le seguenti 2 condizioni:

$(f \circ g)(x) = x \qquad \qquad (g \circ f)(x) = x$

Quindi controlliamo se entrambe le equazioni sono soddisfatte. Per prima cosa controlliamo

$(f \circ g)(x) = x:$

$\begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}$

➤ Se non capisci il calcolo che abbiamo appena fatto, devi andare al link sopra Qual è la composizione delle funzioni? , spieghiamo come risolvere questo tipo di operazioni con le funzioni.

Affinché

$(f \circ g)(x) = x$

sì, è compiuto.

Ora controlliamo l’uguaglianza

$(g \circ f)(x) = x :$

$\begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}$

E la condizione di invertibilità

$(g \circ f)(x) = x$

è anche compiuto.

In conclusione, poiché valgono entrambe le equazioni, le due funzioni sono l’una l’inversa dell’altra.

Di seguito puoi vedere entrambe le funzioni rappresentate graficamente. Si noti che i grafici di due funzioni inverse sono simmetrici rispetto alla bisettrice del primo e del terzo quadrante:

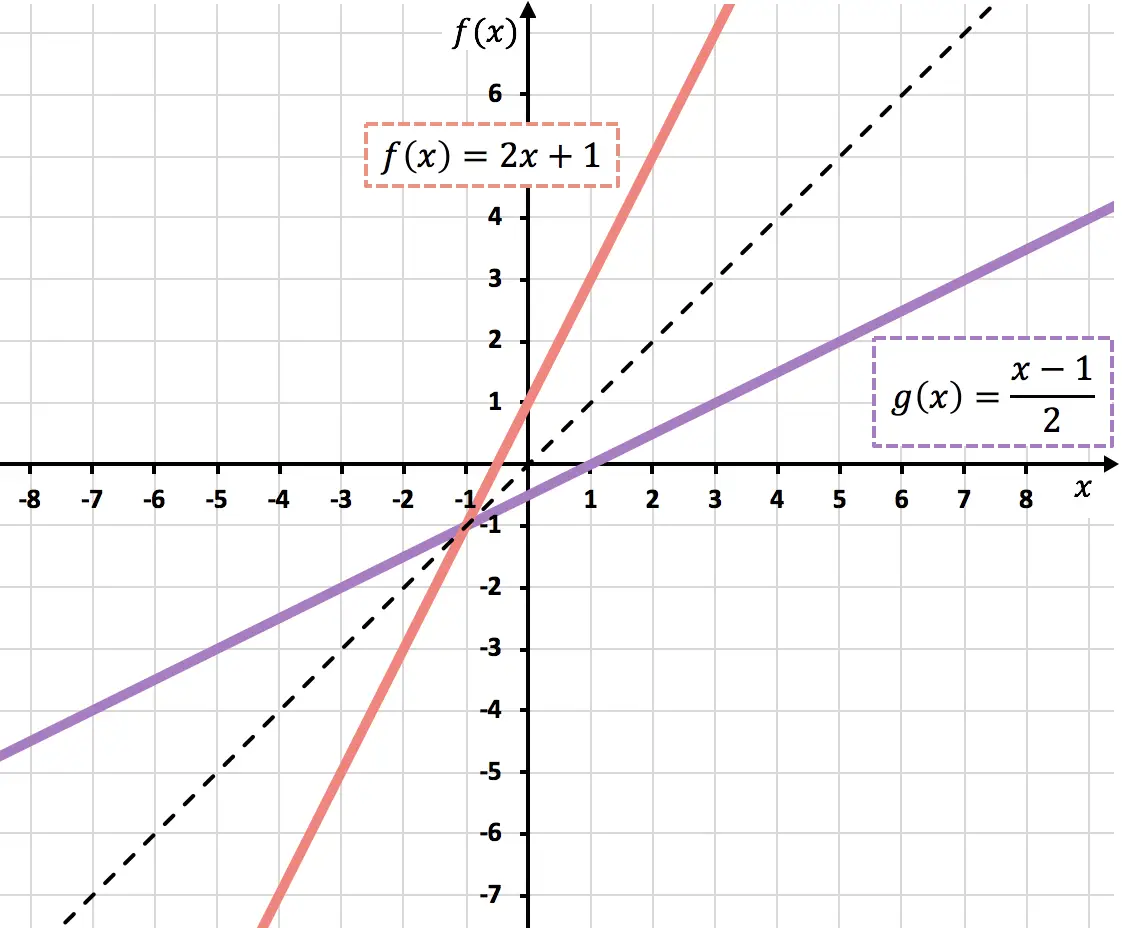
Come sapere se una funzione ha un inverso

Una funzione ha una funzione inversa se è una funzione iniettiva , cioè se ogni valore nel suo intero dominio corrisponde a un singolo valore nel suo intervallo.

Funzione esponenziale con funzione inversa

Funzione quadratica senza funzione inversa

Ad esempio, la funzione esponenziale sinistra ha una funzione inversa perché ogni x corrisponde a un singolo valore di f(x) . D’altra parte, la funzione quadratica destra non ha una funzione inversa poiché ha più valori di x le cui immagini sono uguali (ad esempio f(1)=f(3)=2) .

Allo stesso modo, una funzione biiettiva consiste in una funzione che è sia iniettiva che suriettiva, quindi qualsiasi funzione biiettiva ha anche una funzione inversa.

D’altra parte, dovresti tenere presente che la funzione inversa non è la stessa cosa dell’inverso moltiplicativo di una funzione , ma piuttosto due concetti diversi. Per trovare l’inverso moltiplicativo di una funzione, calcola semplicemente 1 corrispondenza di detta funzione.

$f^{-1}(x) \neq \cfrac{1}{f(x)}$

Nella prossima sezione vedremo come determinare la funzione inversa.

Come trovare la funzione inversa

Per calcolare l’inversa di una funzione è necessario eseguire i seguenti passaggi:

Sostituisci f(x) con y .
Cambia tutto x in y e viceversa.
Cancella la variabile y .
Sostituisci la variabile y con f ^-1 (x) . La funzione inversa è l’espressione trovata per f ^-1 (x) .

Affinché tu possa vedere esattamente come viene calcolata la funzione inversa, determiniamo come esempio l’inversa della seguente funzione:

$f(x) =4x+5$

Prima di tutto dobbiamo sostituire

$f(x)$

Per

$y$

$y=4x+5$

Ora cambiamo tutto

$x$

della funzione di

$y$

, e viceversa:

$y= 4x+5 \quad \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \quad x= 4y+5$

Quindi cancelliamo la variabile

$y:$

$x=4y+5$

$x-5=4y$

$\cfrac{x-5}{4}=y$

$y=\cfrac{x-5}{4}$

E infine, la funzione inversa di

$f(x)$

è l’espressione algebrica che abbiamo ottenuto isolando

$y:$

$\bm{f^{-1}(x) = } \cfrac{\bm{x-5}}{\bm{4}}$

Esercizi risolti della funzione inversa

Di seguito abbiamo preparato diversi esercizi passo passo sulla funzione inversa in modo che tu possa esercitarti.

Ricorda che se non capisci come risolvere un esercizio o vuoi che ti risolviamo un problema, puoi scrivercelo nei commenti!

Esercizio 1

Controlla se le seguenti due funzioni sono inverse (o reciproche) o no:

$f(x)=3x-7\qquad g(x)=\cfrac{x+7}{3}$

Vedi la soluzione

Affinché le due funzioni siano tra loro inverse, deve essere vero quanto segue:

$(f \circ g)(x)=x \qquad \qquad (g \circ f)(x)=x$

È quindi necessario verificare se le due condizioni sono soddisfatte. Per prima cosa controlliamo

$(f \circ g)(x)=x :$

$\begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}$

Ancora,

$(f \circ g)(x) = x$

sì, è compiuto.

Ora controlliamo l’altra composizione delle funzioni

$(g \circ f)(x)=x :$

$\begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}$

Per cui

$(g \circ f)(x) = x$

è anche compiuto.

Come è possibile?

$(f \circ g)(x)=x$

$(g \circ f)(x)=x$

, le due funzioni sono una l’inversa dell’altra.

Esercizio 2

Calcola l’inversa (o funzione reciproca) della seguente funzione polinomiale di primo grado:

$f(x)=-2x-3$

Vedi la soluzione

La prima cosa da fare per invertire la funzione è sostituire il termine

$f(x)$

Per

$}y:$

$y=-2x-3$

Ora cambiamo il

$x$

$y$

, e viceversa:

$y=-2x-3 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =-2y-3$

E poi rilasciamo

$y:$

$x =-2y-3$

$x +3=-2y$

$\cfrac{x +3}{-2}=y$

$y = \cfrac{x +3}{-2}$

Siamo già riusciti a rilasciare

$y$

. Pertanto, la funzione inversa di

$f(x)$

Est:

$\bm{f^{-1}(x) = -} \cfrac{\bm{x+3}}{\bm{2}}$

Esercizio 3

Invertire la seguente funzione polinomiale quadratica:

$f(x)=x^2-1$

Vedi la soluzione

Per trovare la funzione inversa seguiremo il procedimento che abbiamo visto sopra. Quindi chiameremo

$y$

alla funzione

$f(x):$

$y=x^2-1$

In secondo luogo, modifichiamo il file

$x$

per il

$y$

, e viceversa:

$y=x^2-1 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =y^2-1$

E infine isoliamo la variabile

$y:$

$x =y^2-1$

$x+1=y^2$

$\sqrt{x+1}=y$

$y=\pm \sqrt{x+1}$

In questo caso però la funzione ottenuta ha due immagini per ogni elemento del suo dominio (l’immagine positiva e l’immagine negativa). Pertanto non esiste una funzione inversa della funzione problematica.

Esercizio 4

Determinare la funzione inversa (o funzione reciproca) della seguente funzione razionale:

$\displaystyle f(x)=\frac{x-1}{2x+3}$

Vedi la soluzione

Innanzitutto, sostituiamo

$f(x)$

Per

$y:$

$y=\cfrac{x-1}{2x+3}$

Ora cambiamo il

$x$

numeratore e denominatore

$y$

, e viceversa:

$y=\cfrac{x-1}{2x+3} \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x=\cfrac{y-1}{2y+3}$

E poi rilasciamo

$y:$

$x=\cfrac{y-1}{2y+3}$

L’espressione

$2y +3$

divide l’intero lato destro dell’equazione, quindi possiamo moltiplicarlo moltiplicando l’intero lato sinistro dell’equazione:

$x\cdot (2y+3)=y-1$

$2yx+3x=y-1$

Mettiamo tutti i termini con

$y$

da un lato dell’equazione e gli altri termini dall’altro:

$2yx-y=-3x-1$

Per chiarire

$}y$

, estraiamo il fattore comune dal lato sinistro dell’equazione:

$y(2x-1)=-3x-1$

E come postino

$(2x-1)$

è moltiplicare l’intero lato sinistro dell’equazione, possiamo farlo dividendo l’intero lato destro:

$y=\cfrac{-3x-1}{2x-1}$

Siamo già riusciti a rilasciare

$y$

. Quindi la funzione inversa di

$f(x)$

Est:

$\bm{f^{-1}(x)=} \cfrac{\bm{-3x-1}}{\bm{2x-1}}$

Proprietà della funzione inversa

La funzione inversa ha le seguenti caratteristiche:

La funzione inversa è unica, cioè se una funzione è invertibile, per questa funzione esiste una sola funzione inversa.

Il dominio della funzione inversa è l’intervallo (o intervallo) della funzione originale.

Allo stesso modo, il percorso della funzione inversa è equivalente al dominio della funzione originale.

Qualsiasi funzione composta dalla sua funzione inversa dà la funzione identità (x).

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

Il grafico di una funzione e il grafico della sua funzione inversa sono simmetrici rispetto alla bisettrice del primo e del terzo quadrante.

L’inverso della funzione inversa è uguale alla funzione originale:

$\left(f^{-1}\right)^{-1}=f$

Invertire una funzione composta equivale a calcolare l’inversa di ciascuna funzione separatamente e quindi comporre le funzioni inverse.

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Una funzione è contemporaneamente continua con la sua funzione inversa, o in altre parole, se una funzione è continua, lo sarà anche la sua funzione inversa.

Se una funzione è differenziabile e la derivata non scompare in nessun momento
$f'(x)\neq 0$

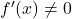
, anche la sua funzione inversa sarà differenziabile.

Inoltre, la derivata della funzione inversa può essere calcolata applicando il teorema della funzione inversa , la cui formula è:

$\left(f^{-1}\right)'(y)=\cfrac{1}{f'(x)}$

Funzione inversa (o reciproca).

Qual è la funzione inversa?

Esempio di funzione inversa

Come sapere se una funzione ha un inverso

Come trovare la funzione inversa

Esercizi risolti della funzione inversa

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Proprietà della funzione inversa

Lascia un commento Annulla risposta