▷ Composizione di funzioni (o funzione composita)

In questo articolo spieghiamo cos’è la funzione composita (o composizione di funzioni). Inoltre, potrai vedere diversi esempi di funzioni composte e come viene calcolato il dominio di questo tipo di funzioni. Infine, troverai le proprietà della composizione delle funzioni e diversi esercizi passo passo per esercitarti.

Cos’è la composizione della funzione?

La composizione della funzione consiste nel valutare successivamente lo stesso valore della variabile indipendente (x) in due o più funzioni. Ad esempio, componendo le funzioni (gof)(x) si ottiene la funzione composta g[f(x)].

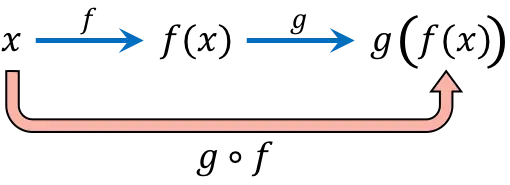
L’espressione della funzione composta

$g\circ f$

si legge “f composta con g” oppure “f seguita da g”.

Tieni presente che l’ordine è importante nella composizione delle funzioni, la funzione a destra del simbolo della composizione viene applicata per prima

$(f)$

poi la funzione a sinistra del simbolo della composizione

$(g).$

Esempio di composizione di funzioni

Data la definizione di funzione composta, vediamo un esempio di come calcolare la composizione di due funzioni.

Date le seguenti due diverse funzioni:

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

Calcola la funzione composta

$\left(g \circ f\right)(x)$

e valutarlo

$x=3.$

La composizione delle funzioni

$\left(g \circ f\right)(x)$

Ciò significa che dobbiamo eseguire la seguente funzione composita:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Per risolverlo, sostituiamo

$f(x)$

dalla sua espressione algebrica:

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

E ora prendiamo la funzione di

$g(x)=\cfrac{x+4}{2}$

e mettiamo l’espressione

$3x+1$

dove ce n’è uno

$x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

In questo modo abbiamo già calcolato la funzione f composta da g :

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

Infine, per valutare la funzione composta in

$x=3$

Basta calcolare l’immagine della funzione in detto valore:

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

Dominio di funzioni composto

Normalmente, quando eseguiamo operazioni sulle funzioni, il dominio della funzione risultante è l’intersezione dei domini delle funzioni originali. Tuttavia, questa proprietà non è soddisfatta dalla composizione della funzione.

Il dominio della composizione delle funzioni

$(g\circ f)(x)$

è equivalente all’insieme di tutti i valori di x nel dominio della funzione

$f$

ad esempio

$f(x)$

appartiene al dominio della funzione

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Pertanto, per calcolare il dominio di una funzione composta, è necessario prima trovare separatamente il dominio di ciascuna funzione, quindi il dominio della funzione risultante dall’operazione. Pertanto il dominio di composizione delle funzioni sarà costituito da tutti i valori che soddisfano la condizione matematica precedente.

Ricorda, se riscontri un problema che non sai come risolvere, puoi chiedercelo nei commenti qui sotto!

Proprietà di composizione delle funzioni

Le funzioni composte hanno le seguenti caratteristiche:

La composizione delle funzioni ha la proprietà associativa, quindi vale sempre la seguente equazione:

$f\circ (g\circ h)=(f\circ g)\circ h$

In generale, la composizione della funzione non è commutativa, quindi l’ordine dell’operazione determina il risultato:

$f\circ g\neq g\circ f$

L’elemento neutro della composizione delle funzioni corrisponde alla funzione identità
$f(x)=x.$

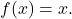
Pertanto, qualsiasi funzione composta con la funzione identità risulta nella funzione stessa:

$f\circ id = id \circ f = f$

$id = x$

Calcolare l’inverso della composizione di due funzioni equivale a trovare prima l’inverso di ciascuna funzione e poi determinare la funzione composta:

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

La funzione inversa funge anche da elemento simmetrico della funzione composta, poiché la composizione di una funzione con la sua inversa equivale alla funzione identità:

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

La derivata della composizione di due funzioni si calcola utilizzando la regola della catena:

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤ Vedi: qual è la regola della catena?

Esercizi risolti sulla composizione delle funzioni

Esercizio 1

Date le seguenti due funzioni:

$f(x)=x-2 \qquad g(x)= 5x + 4$

Calcolare le composizioni delle funzioni f composta con g e g composta con f .

$(g\circ f)(x)$

$(f\circ g)(x)$

Vedi la soluzione

La composizione delle funzioni

$\left(g \circ f\right)(x)$

significa calcolare la seguente funzione composta:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Quindi per risolverlo sostituiamo

$f(x)$

per la sua espressione:

$f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

$g\Big(x-2\Big)$

Ciò significa che nell’espressione di

$g(x) =5x+4$

devi sostituire la variabile

$x$

Per

$x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

Ancora:

$\bm{\left(g \circ f\right)(x) = 5x-6}$

Per trovare invece la funzione g composta da f bisogna eseguire lo stesso procedimento ma con l’ordine inverso:

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

Questo esercizio dimostra anche la proprietà che le funzioni composte non sono commutative, poiché il risultato dipende dall’ordine in cui le funzioni vengono applicate.

Esercizio 2

Date le seguenti due funzioni:

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

Calcola la composizione delle funzioni f composte con g .

$(g\circ f)(x)$

Vedi la soluzione

La funzione f composta da g significa risolvere la seguente funzione composta:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Sostituiamo quindi la funzione f(x) con la sua espressione:

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

E ora dobbiamo sostituire

$x$

Per

$x^2-3$

nell’espressione della funzione g(x):

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

In breve, il risultato della composizione della funzione è:

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

Esercizio 3

Date le seguenti due funzioni quadratiche:

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

Determinare il risultato della seguente composizione di funzioni:

$(g\circ f)(2)$

Vedi la soluzione

$\left(g \circ f\right)(2)$

consiste nel trovare la seguente funzione composta:

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

Quindi per risolvere la funzione composta dobbiamo prima calcolare

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

Pertanto, come

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

Quindi per trovare il valore della funzione composta devi solo calcolare

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

In sintesi, il risultato del problema di composizione della funzione è:

$\bm{\left(g \circ f\right)(2) =8}$

Esercizio 4

Date le seguenti due funzioni:

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

Trova il risultato di g composto con f in x=2:

$(f\circ g)(2)$

Vedi la soluzione

In questo caso dobbiamo calcolare la seguente funzione composta:

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

Quindi prima troviamo

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

E così, tipo

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

Quindi per risolvere la funzione composta dobbiamo calcolare

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$