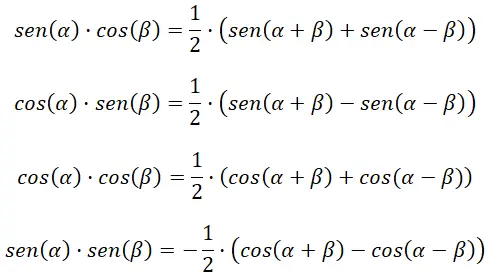Le identità trigonometriche sono uguaglianze tra diverse funzioni trigonometriche. Grazie a queste equivalenze trigonometriche possiamo dedurre un certo rapporto trigonometrico a partire da qualsiasi altro. Pertanto, è necessario conoscere le formule di questi rapporti per comprendere le formule delle identità trigonometriche. Se non li conosci nel tuo caso, ti consigliamo di visitare l’ultimo link.
Tavola delle identità trigonometriche
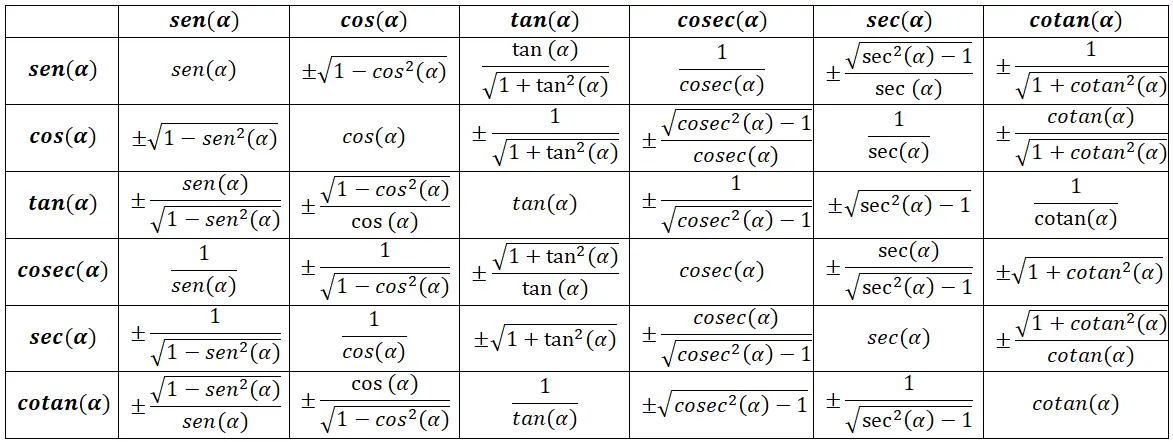
Identità trigonometriche fondamentali
Esistono una serie di identità trigonometriche di base che sono considerate le più importanti perché forniscono la base teorica per le altre. Questi sono i più comuni da trovare e probabilmente i più facili da ricordare, poiché sono abbastanza intuitivi. Ricorda che tutte le formule saranno basate sulla seguente immagine:

Identità trigonometrica fondamentale
La prima identità di tutte è quella conosciuta come identità trigonometrica fondamentale , nota anche come relazione tra seno e coseno. Di seguito la sua dimostrazione matematica: sin² (α) + cos² (α) = 1.
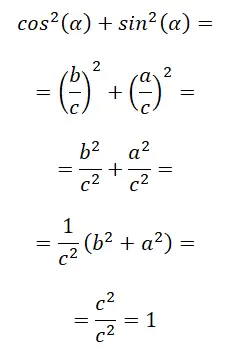
Nell’ultimo passaggio applichiamo sostanzialmente il teorema di Pitagora, poiché c² = a² + b², ci rimane c² / c² che è uguale a 1. In conclusione, possiamo affermare che: sin² (α) + cos² (α) = 1.
Relazione tra secante e tangente (secante al quadrato)
In secondo luogo abbiamo un’identità trigonometrica che mette in relazione la secante con la tangente, la sua espressione è la seguente: sec² (α) = 1 + tan² (α) . Nell’immagine seguente puoi vedere alcune formule di promemoria che compongono questa identità e poi la procedura da seguire per arrivare alla formula finale:
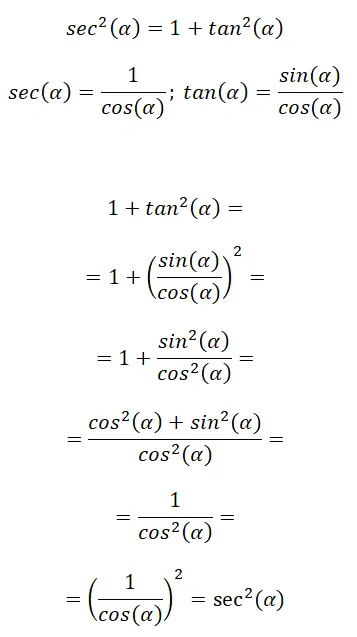
In questo caso, utilizziamo le formule dei rapporti trigonometrici per trovare altri rapporti. In conclusione possiamo dire che: sec²(α) = 1 + tan²(α).
Relazione tra cosecante e cotangente (cosecante al quadrato)
Dalla definizione di cosecante e cotangente possiamo trovare un collegamento nella formula della tangente, è grazie a questo che possiamo dedurre un’altra identità trigonometrica: cosec² (α) = 1 + cotg² (α) .
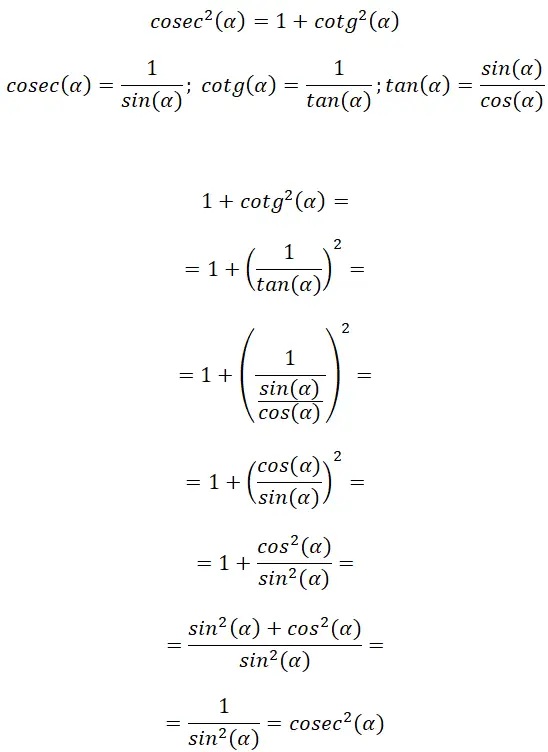
Con questa dimostrazione possiamo verificare che: cosec² (α) = 1 + cotg² (α). Inoltre, possiamo vedere che questa relazione ha qualche somiglianza con la precedente, dovuta alla somiglianza tra tangente e cotangente.
Rapporti trigonometrici dell’angolo di somma e dell’angolo di sottrazione
I rapporti di somma o sottrazione di angoli sono un tipo di identità ottenute calcolando i rapporti trigonometrici dell’addizione o della sottrazione di due angoli. Se ad esempio vogliamo calcolare il seno di 90+60, esistono una serie di formule che facilitano questo calcolo. Di seguito è riportato un elenco con tutte le formule per le identità trigonometriche di questo stile:
Seno della somma degli angoli: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
Seno della sottrazione dell’angolo: sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
Coseno della somma degli angoli: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
Sottrazione del coseno angolare: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
Tangente della somma degli angoli: tan (α + β ) = (tan (α) + tan ( β )) ÷ (1 – tan (α) tan ( β ))
Sottrazione della tangente angolare: tan(α – β ) = (tan(α) + tan( β )) ÷(1 + tan(α)tan( β ))
È ovvio che calcolare il seno di 150º è più semplice che usare le formule che abbiamo appena spiegato per calcolare il seno di (90º + 60º). Allora perché queste formule sono importanti? Ebbene, la risposta è che queste identità ci permettono di calcolare i rapporti trigonometrici di angoli complessi a partire da angoli più semplici. Pertanto, se memorizziamo i rapporti degli angoli notevoli (più rilevanti), non avremo bisogno di usare la calcolatrice per calcolare i rapporti degli angoli più complessi come 150º.
Rapporti trigonometrici a doppio angolo
Quando vogliamo calcolare i rapporti trigonometrici di un doppio angolo (2α) , possiamo farlo mediante una serie di identità. Più precisamente, possiamo farlo attraverso formule molto simili a quelle di cui abbiamo appena parlato nella sezione precedente. Poiché, se cambiamo β in α, nelle espressioni precedenti, ci rimane (α + α), che equivale a (2α). Tenendo presente questo, possiamo ricavare le seguenti identità:
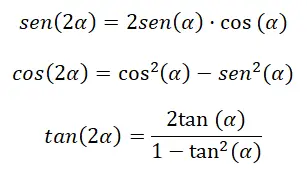
Puoi vedere le demo qui sotto:
Seno del doppio angolo: sin (2α) = sin (α) cos (α) + cos (α) sin (α) = 2 sin (α) cos (α)
Coseno del doppio angolo: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
Doppio angolo tangente: tan (2α) = 2 tan (α) ÷ (1 – tan² (α))
Rapporti trigonometrici del semiangolo
Inoltre, esistono identità che permettono di calcolare i rapporti trigonometrici del semiangolo (α/2) :
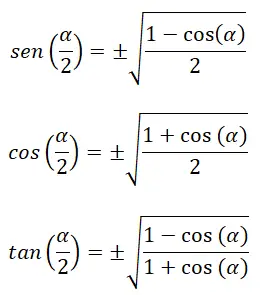
Tra le seguenti formule già note:
1 = sin²( β ) + cos²( β )
cos( 2β ) = cos²( β ) – sin²( β )
Se poniamo β = α/2, allora possiamo dimostrare queste identità, sottraendo le due espressioni nel caso del seno, sommandole nel caso del coseno, e dividendo le due formule ottenute (quella del seno e quella del coseno) nel caso della tangente. Resta però da isolare il rapporto che vogliamo calcolare nelle formule che otteniamo di seguito:
Angolo mezzo seno: 1 – cos (α) = 2 sin² (α/2); sin² (α/2) = (1 – cos (α)) ÷ 2
coseno del semiangolo: 1 + cos (α) = 2 cos² (α/2); cos² (α/2) = (1 + cos (α)) ÷ 2
Rapporti trigonometrici del triplo angolo
Nel caso in cui si abbia un angolo triplo (3α) , possiamo anche utilizzare determinate identità per calcolare i loro rapporti trigonometrici. Queste identità provengono dalle seguenti formule già spiegate: identità del doppio angolo, identità dell’angolo somma e identità fondamentale della trigonometria.
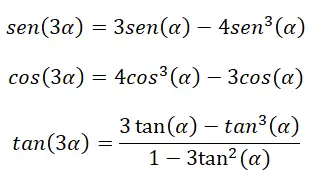
Per dimostrare queste identità, dobbiamo usare le formule di somma degli angoli:
Seno della somma degli angoli: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
Coseno della somma degli angoli: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
Quindi, se applichiamo le formule del doppio angolo nelle espressioni di cui abbiamo appena parlato e applichiamo l’identità fondamentale della trigonometria, possiamo dimostrare le identità. Vale la pena ricordare che l’utilizzo dell’identità trigonometrica fondamentale ci consente di convertire tutti i rapporti nell’espressione in uno solo. Ecco perché la formula del seno del triplo angolo è composta solo da seni e quella del coseno contiene solo coseni. Di seguito potete vedere la procedura completa:
Seno del triplo angolo: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= sin (α) cos² (α) – sin³ (α) + 2 sin (α) cos² (α) =
= sin (α) · (1 – sin² (α)) – sin³ (α) + 2 sin (α) · (1 – sin² (α)) =
= sin (α) – sin³ (α) – sin³ (α) + 2 sin (α) – 2 sin³ (α) =
= 3 sin (α) – 4 sin³ (α)
Coseno del triplo angolo: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos (α) (cos² (α) – sin² (α)) – sin (α) 2 sin (α) cos (α) =
= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =
= cos³ (α) – 3 cos (α) + 3 cos³ (α) =
= 4 cos³ (α) – 3 cos (α)
Infine, la tangente del triplo angolo può essere calcolata in due modi: il primo dividendo la formula del seno per la formula del coseno e il secondo sostituendo l’espressione della tangente del doppio angolo, nella seguente formula alla tangente dell’angolo angolo somma: tan (α + 2α) = (tan (α) + tan (2α)) ÷ (1 – tan (α) tan (2α)).
Identità trigonometriche secondo il tipo di angolo
È importante commentare una serie di formule che sono in un certo senso regole che permettono il calcolo diretto e rapido dei rapporti trigonometrici. Esse infatti possono essere considerate anche identità trigonometriche, poiché rispettano le stesse caratteristiche di tutte le espressioni di cui abbiamo appena parlato. Più precisamente, queste formule permettono di determinare le relazioni trigonometriche di un angolo a partire dal rapporto che ha con un altro angolo.
angoli complementari
Gli angoli complementari (α e β ) sono quelli la cui somma è pari a 90º, quindi sommandoli otteniamo un angolo retto. Per determinare che α è l’angolo complementare di β , dobbiamo risolvere un’equazione molto semplice: α = 90 – β , se il risultato di questa equivalenza concorda, allora possiamo affermare che sono complementari. Grazie a queste identità possiamo dedurre i rapporti trigonometrici di un angolo da quelli dell’altro.
Seno dell’angolo complementare: sin (90º – α) = cos (α)
Coseno dell’angolo complementare: cos (90º – α) = sin (α)
Tangente dell’angolo complementare: tan (90º – α) = cotan (α)
Cosecante dell’angolo complementare: cosec (90º – α) = sec (α)
Secante dell’angolo complementare: sec (90º – α) = cosec (α)
Cotangente dell’angolo complementare: cotan (90º – α) = tan (α)
angoli aggiuntivi
Gli angoli supplementari (α e β ) sono quelli che hanno una somma pari a 180º o π radianti, si può quindi dedurre la formula α + β = 180º. Ovvero, in altre parole, se l’angolo supplementare di α è β , allora deve essere soddisfatta la seguente espressione β = 180 – α . Quindi puoi vedere l’elenco delle identità che possiamo dedurre da questi punti di vista:
Seno dell’angolo supplementare: sin (180º – α) = sin (α)
Coseno dell’angolo aggiuntivo: cos (180º – α) = -cos (α)
Tangente dell’angolo supplementare: tan (180º – α) = -tan (α)
Cosecante dell’angolo aggiuntivo: cosec (180º – α) = cosec (α)
Secante dell’angolo supplementare: sec (180º – α) = -sec (α)
Cotangente dell’angolo supplementare: cotan (180º – α) = -cotan (α)
angoli coniugati
Gli angoli coniugati (α e β ) sono quelli la cui somma è pari a 360º ovvero 2π radianti, da cui si ricava la formula α + β = 360º. E da questa prima formula possiamo esprimere uno degli angoli in termini dell’altro come segue: α = 360º – β oppure β = 360º – α. Ora ti mostreremo le uguaglianze degli angoli coniugati:
Seno dell’angolo coniugato: sin (360º – α) = – sin (α)
Coseno dell’angolo coniugato: cos (360º – α) = cos (α)
Tangente dell’angolo coniugato: tan (360º – α) = – tan (α)
Cosecante dell’angolo coniugato: cosec (360º – α) = – cosec (α)
Secante dell’angolo coniugato: sec (360º – α) = sec (α)
Cotangente dell’angolo coniugato: cotan (360º – α) = – cotan (α)
angoli opposti
Gli angoli opposti o negativi (α e β ) sono quelli che hanno lo stesso valore numerico, ma hanno segni diversi, un esempio di questo tipo di angolo è 30º e -30º. Va ricordato che il segno negativo indica che la rotazione è in senso orario, mentre un angolo positivo ruota in senso antiorario.
Seno dell’angolo opposto: sin (-α) = – sin (α)
Coseno dell’angolo opposto: cos (-α) = cos (α)
Tangente dell’angolo opposto: tan (-α) = – tan (α)
Cosecante dell’angolo opposto: cosec (-α) = – cosec (α)
Secante dell’angolo opposto: sec (-α) = sec (α)
Cotangente dell’angolo opposto: cotan (-α) = – cotan (α)
Angoli che differiscono da 90º o angoli più/meno π/2
Gli angoli che differiscono di 90º o gli angoli più/meno π/2 (α e β ) sono quelli che hanno una differenza di 90º. Pertanto, possono essere espressi come β – α = 90º, dove β è 90º maggiore di α . Questi angoli hanno anche una serie di formule che mettono in relazione i rapporti trigonometrici dei due angoli.
Seno dell’angolo diverso da 90º: sin (90º + α) = cos (α)
Coseno dell’angolo diverso da 90º: cos (90º + α) = -sin (α)
Tangente dell’angolo diverso da 90º: tan (90º + α) = – cotan (α)
Cosecante dell’angolo diverso da 90º: cosec (90º + α) = sec (α)
Secante dell’angolo diverso da 90º: sec (90º + α) = -cosec (α)
Cotangente dell’angolo diverso da 90º: cotan (90º + α) = -cotan (α)
Angoli che differiscono da 180º o angoli più/meno π
Gli angoli più/meno π (α e β ) equivalgono ad angoli che differiscono di 180º. Pertanto possono essere espressi utilizzando la seguente formula: β – α = 180º, dove β 180º è maggiore di α . Successivamente, ti mostriamo le identità trigonometriche che mettono in relazione i rapporti trigonometrici di questi angoli:
Seno dell’angolo diverso da 180º: sin (180º + α ) = -sin ( α )
Coseno dell’angolo diverso da 180º: cos (180º + α ) = -cos ( α )
Tangente dell’angolo diverso da 180º: tan (180º + α ) = tan ( α )
Cosecante dell’angolo diverso da 180º: cosec (180º + α ) = -cosec ( α )
Secante dell’angolo diverso da 180º: sec (180º + α ) = -sec ( α )
Cotangente dell’angolo diverso da 180º: cotan (180º + α ) = cotan ( α )
Trasformazioni di rapporti trigonometrici
Infine, ci sono identità trigonometriche che ci permettono di esprimere un certo rapporto trigonometrico mediante altre operazioni . Quindi se abbiamo una somma di rapporti e vogliamo esprimerla come prodotto, possiamo ricorrere a queste formule. Anche se purtroppo non esiste un’espressione per ogni operazione aritmetica, si può solo passare dall’addizione o dalla sottrazione al prodotto e viceversa .
Converti addizione o sottrazione in prodotto
Le seguenti quattro formule ci aiutano a calcolare l’addizione e la sottrazione delle funzioni trigonometriche:
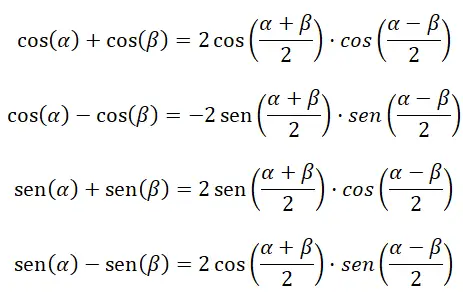
Trasforma il prodotto in addizione o sottrazione
Le seguenti quattro formule ci aiutano a calcolare i prodotti delle funzioni trigonometriche: