I rapporti trigonometrici di un angolo sono i rapporti ottenuti dai tre lati di un triangolo rettangolo. In altre parole, questi sono i valori che risultano dal confronto dei suoi tre lati utilizzando i quozienti (divisioni). Anche se va notato che questi motivi esistono solo nei triangoli rettangoli (triangoli che hanno un angolo di 90º).
Rapporti trigonometrici in un triangolo rettangolo
I sei rapporti trigonometrici più importanti sono: seno, coseno, tangente, cosecante, secante e cotangente. Successivamente, spiegheremo nel dettaglio come viene definito ciascuno di questi motivi e parleremo della formula che li caratterizza. Per comprendere le seguenti spiegazioni prenderemo in considerazione il seguente triangolo rettangolo:

Seno
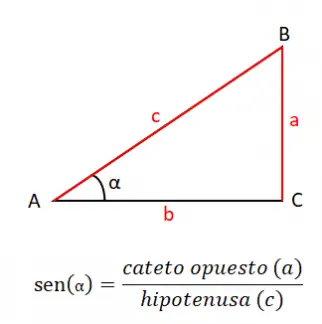
Il seno di un angolo (sin o sin) è uguale al quoziente del cateto opposto (a) tra l’ipotenusa (c), pertanto la formula del seno è: sin (α) = a / c . È molto importante conoscere questa definizione di seno, perché è la base di tutta la trigonometria, insieme agli altri motivi che tratteremo in questa sezione.
Trav È dal teorema del seno che possiamo calcolare qualsiasi lato del triangolo , possiamo farlo collegando i quozienti di un certo angolo tra il suo lato corrispondente. Ad esempio, se vogliamo calcolare il lato a e abbiamo i valori dei lati per gli angoli A e B, possiamo farlo utilizzando la formula: a/sen (A) = b/sen (B) . Risolvendo questa semplice equazione otteniamo il valore corrispondente alla variabile che vogliamo calcolare.
Coseno
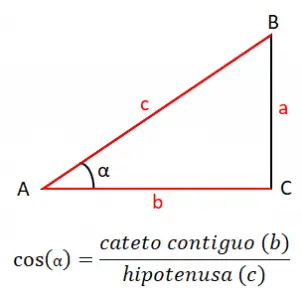
Il coseno di un angolo (cos) è uguale al quoziente del cateto adiacente (b) tra l’ipotenusa (c), quindi la formula del coseno è: cos (α) = b / c . In questo caso la formula è composta dai due lati del triangolo che sono in contatto con l’angolo che vogliamo studiare, in questo esempio l’angolo A o α.
Con il coseno abbiamo anche un modo per calcolare i lati del triangolo , che deriva dal teorema del coseno. Questo ci permette di collegare i lati agli angoli e ci dà le seguenti tre espressioni:
a² = b² + c² – 2bc cos (A)
b² = a² + c² – 2ac cos (B)
c² = a² + b² – 2ab cos (C)
Tangente
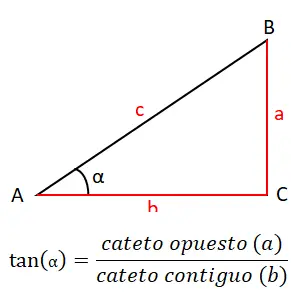
Il terzo motivo più importante, con cui chiuderemo l’insieme dei motivi originali, è la tangente (tan o tg). Questo si calcola dividendo tra la gamba opposta (a) e la gamba adiacente (b), quindi la formula della tangente è: tan (α) = a / b . Puoi vederlo graficamente qui sotto:
Anche la tangente ha un suo teorema, chiamato teorema della tangente. Questo ci permette di mettere in relazione le lunghezze di due lati di un triangolo con le tangenti degli angoli . L’affermazione è la seguente: “il quoziente della somma di due lati tra la loro sottrazione è pari al quoziente tra la tangente della media dei due angoli opposti a tali lati e la tangente della metà della differenza di questi” .
Rapporti trigonometrici derivati
Dai tre rapporti trigonometrici appena discussi si possono ricavare altri rapporti trigonometrici derivati. Questi si ottengono prendendo il rapporto inverso rispetto a seno, coseno e tangente.
- Cosecante: è il rapporto inverso del seno e si calcola con le formule: cosec (α) = c/a e cosec (α) = 1/sen (α).
- Secante: è il rapporto inverso del coseno e si calcola con le formule: sec (α) = c / b e sec (α) = 1 / cos (α).
- Cotangente: è il rapporto inverso della tangente e si calcola con le formule: cotg (α) = b/a e cotg (α) = 1/tan (α).
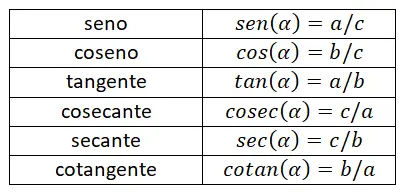
Tabella dei rapporti trigonometrici
Di seguito potete vedere una tabella che riassume tutte le motivazioni finora spiegate. Con questa tabella potrai memorizzare tutte le formule in modo efficace, perché ti permette di distinguere facilmente le differenze tra ogni espressione matematica.
Rapporti trigonometrici in un cerchio
Un altro modo per studiare la trigonometria è attraverso la circonferenza goniometrica o cerchio unitario , questa circonferenza ha raggio pari a 1 e la sua origine è il punto (0, 0). Il disegno è composto da un cerchio e da un triangolo rettangolo raffigurato all’interno del cerchio, più precisamente l’angolo che andremo a studiare deve toccare il punto originale.
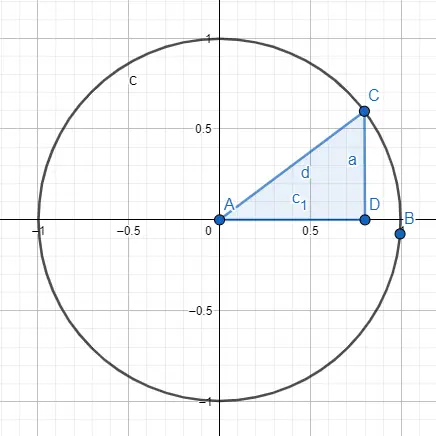
Quando abbiamo questa immagine, sappiamo che il raggio è uguale all’ipotenusa, che è uguale a 1. Quindi, se vogliamo calcolare il seno e il coseno, utilizzeremo il valore del raggio e il valore degli altri lati di il triangolo. Per calcolare il seno, faremo il seguente calcolo: sin (A) = CD / AC = CD / raggio = CD / 1 = CD , quindi il seno di A è a. Invece, per calcolare il coseno, faremo il calcolo: cos (A) = AD / AC = AD / raggio = AD / 1 = AD , quindi il coseno di A è c1.
È molto importante tenere a mente due cose. La prima è che l’uso di questo cerchio nello studio dei rapporti trigonometrici è dovuto alla necessità di trattare angoli maggiori di quelli studiabili con il triangolo. Ad esempio, l’angolo di 150º non può essere studiato attraverso un semplice triangolo, perché è troppo grande. E la seconda cosa da tenere presente è che seno e coseno non possono mai assumere valori maggiori di 1 e minori di -1.
Segno dei rapporti trigonometrici
Come abbiamo detto prima, per trattare angoli più grandi di quanto un triangolo ci permette di trattare, utilizziamo la circonferenza goniometrica. Per fare questo rappresentiamo un triangolo interno al cerchio esattamente in uno dei quattro quadranti che dividono la circonferenza, nell’immagine seguente potete vedere i quattro quadranti rappresentati.
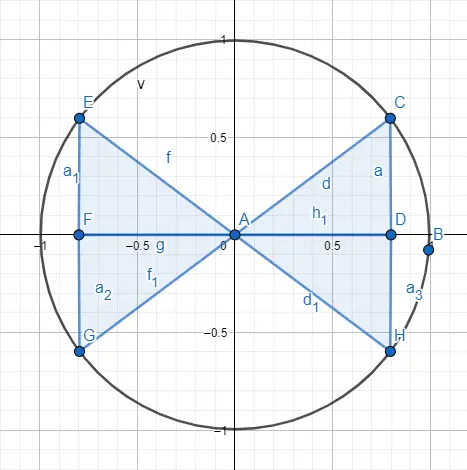
Quindi distinguere tra un angolo di 30 e uno di 210, che diventano la stessa cosa riguardo alla distribuzione all’interno del triangolo , utilizzeremo una distribuzione dei segni in base al quadrante in cui si trova il triangolo. Di seguito potete vedere i segni corrispondenti ad ogni quadrante ed un esempio disegnato.
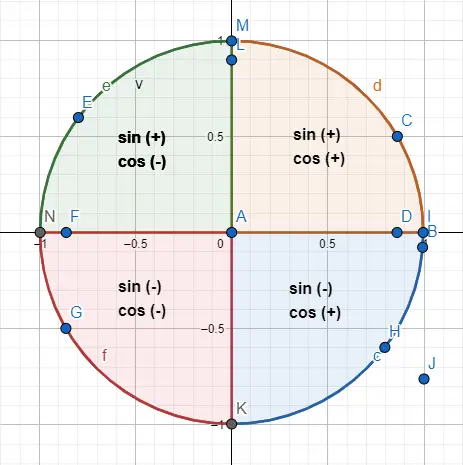
Ad esempio, gli angoli 30º e 210º condividono lo stesso valore numerico , ma il loro seno e coseno hanno segni opposti. Quindi: sin(30) = 1/2 e cos(30) = √3/2, mentre sin(210) = -1/2 e cos(210) = -√3/2. Per ottenere questo risultato abbiamo rappresentato i due angoli sulla circonferenza (immagine sotto) e abbiamo seguito le indicazioni dei segni.
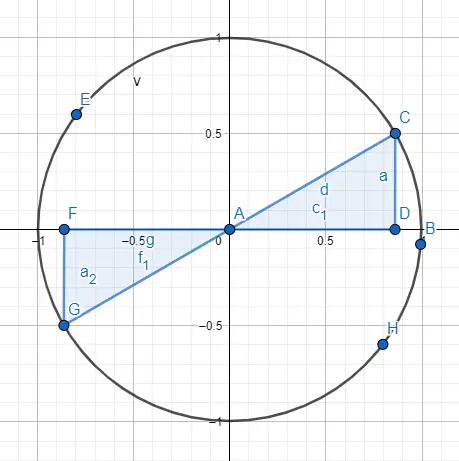
Infine, come è possibile avere angoli maggiori di 360º , anche se potrebbe non sembrare perché la circonferenza è solo di 360º. Ma, se vogliamo trovare un angolo di 750º, possiamo ridurre ad un angolo compreso tra 0º e 360º. Semplicemente dividiamo 750 per 360 e il resto è l’angolo rimanente, nel caso di 750º otteniamo un angolo di 30º.
Tipi di angoli a seconda del quadrante
Esistono relazioni tra diversi angoli, che ci consentono di calcolare i rapporti valori trigonometrici di tutti gli angoli appartenenti al cerchio. Cerchiamo di ottenere queste ragioni della riduzione al primo quadrante . Ciò significa che facciamo una semplificazione da un certo angolo al primo quadrante e poi applichiamo i segni corrispondenti. Di seguito troverete spiegate le diverse procedure (a seconda del quadrante):
primo quadrante
In questo primo quadrante (0º – 90º), dobbiamo solo risolvere la relazione trigonometrica con l’angolo che ci viene dato. E se guardiamo l’immagine che abbiamo spiegato prima sui simboli, seno e coseno hanno davanti a sé un positivo (il risultato che otterremo non sarà influenzato dal segno).
Riduzione dal secondo quadrante al primo
Nel secondo quadrante (90º – 180º) abbiamo a che fare con angoli supplementari, ciò significa che la somma dei due angoli dà 180º. Dobbiamo quindi fare una riduzione dal secondo quadrante al primo e lo facciamo con la formula 180 – α = β , dove α è l’angolo del primo quadrante e β è l’angolo originale.
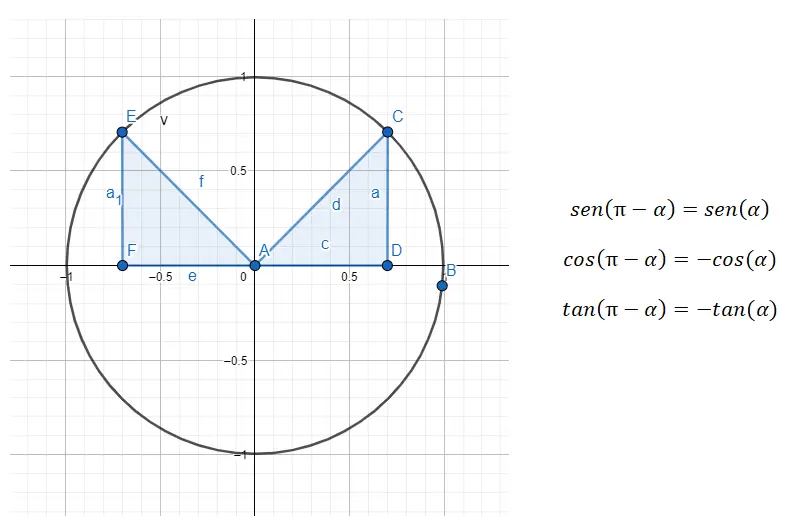
Ad esempio, se ci viene dato l’angolo 135º (che appartiene al secondo quadrante), dobbiamo trovare l’angolo del primo quadrante che è correlato a questo primo. In questo esempio, l’angolo (α) che stiamo cercando è 45º, poiché 180 – 45 = 135. Quindi sarà vero: sin (135) = sin (180 – 45) = sin (45), cos (135 ) = cos (180 – 45) = -cos (45) e tan (135) = tan (180 – 45) = -tan (45).
Riduzione del terzo quadrante al primo
Nel terzo quadrante (180º – 270º) , abbiamo a che fare con angoli che differiscono di 80º, il che significa che gli angoli sono distanti 180º. Quindi se vogliamo ridurre dal terzo quadrante al primo dobbiamo usare la formula 180 + α = β , dove α è l’angolo del primo quadrante e β è l’angolo originale.
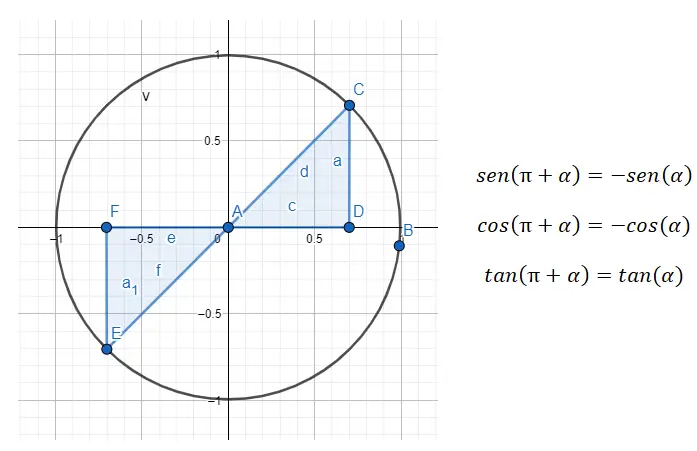
Ad esempio, se ci viene dato l’angolo 225º (che appartiene al terzo quadrante), dobbiamo trovare l’angolo del primo quadrante che gli corrisponde. Nel caso di 225º, l’angolo (α) che stiamo cercando è ancora 45º, poiché 180 + 45 = 225. Quindi, sin (225) = sin (180 + 45) = -sin (45), cos (225) = cos (180 + 45) = -cos (45) e tan (225) = tan (180 + 45) = tan (45) saranno soddisfatti. ).
Riduzione del quarto quadrante al primo
Nel quarto quadrante (270º – 360º) abbiamo a che fare con angoli opposti, il che significa che gli angoli sono numericamente uguali, ma di segno opposto , come 30º e -30º (equivalente a 330º, poiché 360º – 30º = 330º) . È importante tenere presente che gli angoli opposti possono essere scritti come un angolo positivo e un angolo negativo o come due angoli positivi (nell’esempio appena discusso, abbiamo spiegato la differenza).
Quindi se vogliamo fare una riduzione dal quarto quadrante al primo, dobbiamo usare la formula 360 – α = β , dove α è l’angolo del primo quadrante e β è l’angolo originale.
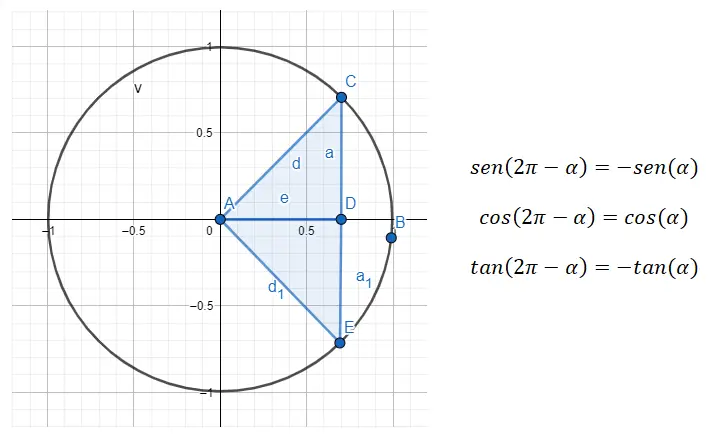
Ad esempio, se ci viene dato l’angolo 315º (che appartiene al quarto quadrante), dobbiamo trovare l’angolo del primo quadrante che è correlato per primo a questo. Nel caso dell’angolo (α) che stiamo cercando, è ancora 45º, poiché 360 – 45 = 315. Quindi sin (315) = sin (360 – 45) = -sin (45), cos ( 315 ) = cos (360 – 45) = cos (45) e tan (315) = tan (360 – 45) = -tan (45). In conclusione, abbiamo visto gli angoli derivati dai 45º di tutti i quadranti.
Rapporti trigonometrici degli angoli più importanti
Esistono numerosi angoli, chiamati angoli notevoli , che sono più comuni in trigonometria. È altamente raccomandato conoscere a memoria i rapporti trigonometrici. Pertanto di seguito abbiamo creato una tabella contenente i rapporti trigonometrici di questi angoli e le loro derivate (stessi angoli, ma con una differenza di 90, 180 o 270 gradi):
| Angolo (°) | Angolo (rad) | Seno | Coseno | Tangente |
| 0º | 0 rad | 0 | 1 | 0 |
| 30º | 1/6 πrad | 1/2 | √3/2 | √3/3 |
| 45º | 1/4 πrad | √2/2 | √2/2 | 1 |
| 60º | 1/3 πrad | √3/2 | 1/2 | √3 |
| 90º | 1/2πrad | 1 | 0 | ∞ |
| 120º | 5/8πrad | √3/2 | -1/2 | -√3 |
| 135º | 3/4 πrad | √2/2 | -√2/2 | -1 |
| 150º | 5/8πrad | 1/2 | -√3/2 | -√3/3 |
| 180º | πrad | 0 | -1 | 0 |
| 225º | 5/4 πrad | -√2/2 | -√2/2 | 1 |
| 270º | 3/2πrad | -1 | 0 | ∞ |
| 315º | 7/4 πrad | -√2/2 | √2/2 | -1 |
Relazione tra rapporti trigonometrici
Esistono diversi modi per mettere in relazione i diversi rapporti trigonometrici. Da queste relazioni otteniamo una sorta di uguaglianze tra le diverse funzioni trigonometriche, che chiamiamo identità trigonometriche. Grazie a questo tipo di identità possiamo calcolare un rapporto basato su qualsiasi altro. Va notato che esistono molti tipi diversi di identità trigonometriche, che vengono classificate in base al tipo di relazione che supporta l’espressione stessa.
Problemi risolti sui rapporti trigonometrici
Successivamente, ti proponiamo una serie di esercizi con i quali potrai mettere in pratica tutta la teoria spiegata in questo articolo. Ricorda che se in qualsiasi momento rimani bloccato o hai domande, puoi rileggere l’articolo e sicuramente, con una seconda lettura , capirai tutto molto meglio. Detto questo, puoi iniziare a praticare:
Esercizio 1
Calcola i sei rapporti trigonometrici dell’angolo 225º:
Inizieremo calcolando l’angolo (α), che è uguale a: 180 + α = 225º, quindi α = 45º.
sin(225) = sin(180 + 45) = -sen(45) = -√2/2
cos(225) = cos(180 + 45) = -cos(45) = -√2/2
tan(225) = tan(180 + 45) = tan(45) = 1
Esercizio 2
Calcola i sei rapporti trigonometrici dell’angolo 120º:
Inizieremo calcolando l’angolo (α), che è pari a: 180 – α = 120º, quindi α = 60º.
sin(120) = sin(180 – 60) = sin(60) = √3/2
cos(120) = cos(180 – 60) = -cos(60) = -1/2
tan(120) = tan(180 – 60) = -tan(60) = -√3
Esercizio 3
Calcola i sei rapporti trigonometrici dell’angolo 510º:
Prima di iniziare, è necessario effettuare la riduzione dell’angolo: 510 / 360 = 1 giro e un angolo rimanente di 150. Successivamente calcoliamo l’angolo (α), che è uguale a: 180 – α = 150, quindi α = 30º.
peccato(150) = peccato(180 – 30) = peccato(30) = 1/2
cos(150) = cos(180 – 30) = -cos(30) = -√3/2
tan(150) = tan(180 – 30) = -tan(30) = -√3/3