Les fractions ou les nombres fractionnaires sont des expressions numériques qui indiquent une quantité divisée par une autre. C’est donc une valeur représentée par le quotient de deux nombres. Avec ce type de nombres, nous pouvons exprimer des quantités décimales et entières et nous pouvons même indiquer des proportions . Ensuite, nous définirons les fractions de manière plus mathématique et nous vous montrerons quelques exemples, afin que vous compreniez graphiquement ce concept.
Que sont les fractions ?
Une fraction est égale au nombre de parties que nous prenons d’une unité qui est divisée en parties égales. Ainsi, graphiquement, il est représenté par deux termes séparés par une ligne horizontale au milieu. Plus précisément, en haut de la ligne, nous trouvons le numérateur et en dessous le dénominateur.
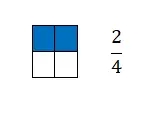
Comme vous pouvez le voir, les fractions sont un concept mathématique très facile à représenter graphiquement , car elles vont de pair avec les proportions. C’est pourquoi dans l’exemple précédent nous avons exprimé le nombre de carrés colorés avec un nombre fractionnaire.
Termes fractionnaires
Les deux parties de la fraction sont :
- Numérateur : Ce terme est situé au-dessus de la ligne horizontale et c’est là que nous écrivons le nombre de pièces que nous prenons. Nous pouvons trouver des numérateurs positifs, négatifs et nuls (égaux à zéro).
- Dénominateur : cet autre terme est situé sous la ligne et c’est là que nous écrivons le nombre total de parties dans lesquelles l’unité est divisée. Nous pouvons trouver des dénominateurs positifs et négatifs, mais ceux-ci ne peuvent pas être nuls.
types de fractions
Il existe de nombreuses sortes de fractions, selon les nombres qui la composent et selon l’équivalence qu’elles présentent avec d’autres fractions. Ensuite, nous définirons toutes les catégories qui existent et nous commenterons les caractéristiques qui permettent de les différencier des autres :
- Fractions propres : sont celles qui sont formées par un numérateur inférieur au dénominateur. Si vous convertissez ces fractions en un nombre décimal , vous obtiendrez un nombre compris entre zéro et un. Il ne peut pas être supérieur à un, car la valeur du numérateur sera toujours inférieure à celle du dénominateur et, par conséquent, l’unité ne sera pas dépassée.
- Fractions impropres: sont celles qui ont un numérateur supérieur au dénominateur, dans ce cas elles expriment des valeurs numériques supérieures à l’unité. Comme par exemple, 8/5 est égal à 1,6 qui est supérieur à 1. Ce sont une autre façon d’exprimer les nombres mixtes, qui sont le type suivant.
- Fractions mixtes : également appelées nombres mixtes, sont celles qui sont composées d’un nombre entier et d’un nombre fractionnaire. Fondamentalement, ils sont représentés avec la valeur entière avant la fraction, donc pour les convertir en fractions impropres, vous devez multiplier la partie entière par le dénominateur, l’ajouter au numérateur et laisser le même dénominateur.
- Fractions décimales : sont celles qui ont un dénominateur qui exprime une quantité équivalente à une puissance de dix, par exemple : 6/10, 34/1000 ou 5/100. Ceux-ci sont utilisés dans la notation décimale et sont les plus courants lors de la conversion de nombres décimaux exacts en nombres fractionnaires. Nous en discuterons plus en détail dans la section suivante.
- Fractions composées : sont celles qui sont composées d’une autre fraction, soit au numérateur, soit au dénominateur, soit dans les deux. Donc, pour simplifier ces expressions et les montrer comme une seule fraction, nous devons diviser le numérateur par le dénominateur. Cela deviendra plus clair une fois que nous aurons expliqué la division entre les fractions.
- Fractions équivalentes : sont celles qui sont équivalentes au même nombre, bien qu’elles ne soient pas constituées des mêmes numérateurs ou dénominateurs. Par exemple, 8/4 = 4/2 = 2, les deux fractions sont égales à deux. Dans ce cas précis, c’est parce que la première fraction est égale à deux fois la seconde, donc, elle maintient une relation proportionnelle.
- Fractions irréductibles : ce sont celles qui ne peuvent pas être simplifiées davantage, car le numérateur et le dénominateur ne partagent pas de facteurs communs et, par conséquent, ne peuvent être divisés par aucun nombre. Quelques exemples de ce type sont : 9/5, 5/6, 7/8, entre autres. Pour savoir les détecter, il est important de savoir calculer le plus grand diviseur commun .
Opérations avec des fractions
Maintenant que nous connaissons les différentes catégories de fractions qui existent, nous allons voir comment résoudre les différentes opérations arithmétiques avec des nombres fractionnaires . Il convient de noter que c’est un peu plus compliqué que les opérations avec des nombres entiers, même si une fois que vous avez compris la méthodologie, tout est assez facile. De plus, nous n’expliquerons pas seulement la théorie, mais nous vous montrerons également quelques exemples. Cela dit, commençons.
somme de fractions
L’ addition de fractions avec un dénominateur commun est assez simple, puisqu’il suffit d’additionner les deux numérateurs et de laisser le même dénominateur. D’un autre côté, ajouter des fractions avec des dénominateurs différents devient un peu délicat, car vous devez trouver le plus petit commun multiple des dénominateurs. Et puis, il faut additionner le produit de chaque numérateur par la division du lcm (le nouveau dénominateur) par l’ancien dénominateur. Pour mieux comprendre, vous pouvez regarder le schéma suivant :
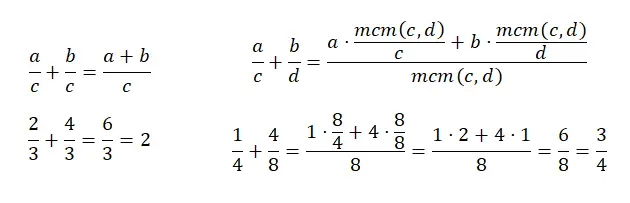
fractions de soustraction
La soustraction de fractions avec un dénominateur commun est très similaire à l’addition, en fait tout se fait de la même manière sauf dans la somme des numérateurs, car au lieu d’additionner, il faut soustraire. Et dans la soustraction de fractions avec des dénominateurs différents, la même chose se produit, c’est pratiquement la même chose sauf qu’au lieu d’ajouter le produit des numérateurs par la division du lcm par l’ancien dénominateur, il faut soustraire. Voici un autre schéma :
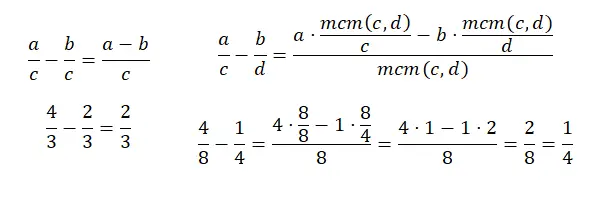
multiplication de fractions
La multiplication de fractions peut être résolue de la même manière, que les dénominateurs soient identiques ou non. En gros, il faut multiplier les numérateurs par une partie et les dénominateurs par une autre. C’est peut-être l’opération la plus simple, puisque vous n’avez qu’à effectuer deux multiplications.
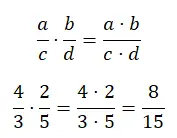
division de fractions
La division en fractions est également assez facile à résoudre, il vous suffit de multiplier les croix. En d’autres termes, le numérateur est le résultat de la multiplication du numérateur de la première fraction par le dénominateur de la seconde. Alors que le dénominateur est le produit du dénominateur de la première fraction et du numérateur de la seconde.
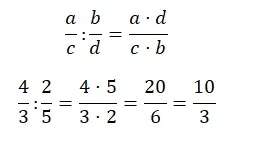
Simplifier des fractions
Simplifier des fractions ou réduire des fractions n’est pas une opération arithmétique en tant que telle, mais il est très important de savoir comment le faire et aussi, c’est un sujet que nous avons déjà un peu abordé avec les types de fractions. Ainsi, pour simplifier un nombre fractionnaire, nous devons diviser le numérateur et le dénominateur par le même nombre. Généralement, on choisira le plus grand facteur commun pour faire cette simplification. Dans l’image suivante, vous pouvez trouver un exemple.
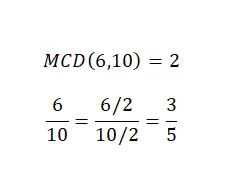
Comme vous pouvez le voir, nous avons deux fractions équivalentes , donc les deux représentent la même valeur numérique, mais la seconde est plus simple que la première. Par conséquent, nous avons atteint l’objectif de simplification avec succès.
Comment passer du nombre décimal à la fraction et inversement ?
La fraction génératrice est la fraction irréductible obtenue à partir d’un nombre décimal, soit un nombre décimal exact, soit un nombre décimal répétitif. Bien sûr, nous devrons utiliser différentes méthodes en fonction du type de décimal, ce dont nous allons discuter ci-dessous.
Convertir de la décimale exacte en fraction génératrice
Dans ce cas, nous pouvons recourir aux fractions décimales que nous avons commentées au début. Simplement, nous devons écrire la valeur numérique au numérateur, mais sans la virgule. Alors qu’au dénominateur on écrit la puissance de dix qui a autant de zéros qu’il y a de chiffres au numérateur.
Cependant, si nous avons un nombre décimal supérieur à un, tel que 4,25, nous devrons alors multiplier le nombre d’unités complètes que nous avons par la valeur du dénominateur et l’ajouter au numérateur d’origine. Ci-dessous, vous trouverez un exemple de chaque type :
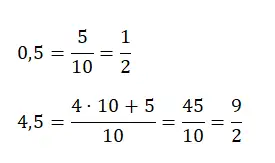
Convertir de la décimale répétitive pure en fraction génératrice
Lorsque nous avons un nombre décimal périodique pur , si nous voulons obtenir la fraction génératrice, nous devrons mettre la même valeur au numérateur, mais sans point décimal et soustraire la partie entière. Alors que le dénominateur sera égal à un nombre formé uniquement de neuf, nous devons en particulier écrire autant de neuf que le nombre de chiffres que comporte la partie décimale du nombre d’origine. Ce système est quelque peu déroutant, mais avec quelques exemples, on comprendra :
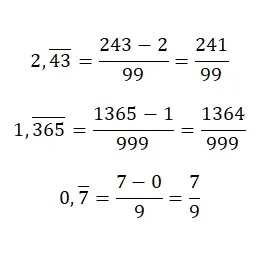
Convertir des nombres décimaux répétés mixtes en fractions génératrices
En cas d’avoir un nombre décimal répété mixte , nous devrons appliquer une règle assez complexe. Premièrement, nous écrirons le nombre sans la virgule au numérateur et nous soustrairons la partie entière suivie des décimales non récurrentes, également sans virgule. Quant au dénominateur, il faudra écrire autant de neufs qu’il y a de chiffres dans la partie décimale périodique, suivis d’autant de zéros qu’il y a de chiffres dans la partie décimale non récurrente.
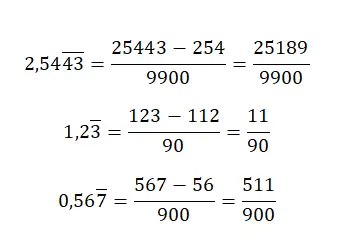
convertir de fraction en décimal
Pour passer d’une fraction à une décimale, il suffit de diviser le numérateur par le dénominateur, car un nombre fractionnaire n’est rien de plus que le quotient entre deux valeurs . Ainsi, en résolvant la division, vous obtenez le nombre décimal correspondant. Dans l’image suivante, vous pouvez trouver quelques exemples assez simples :
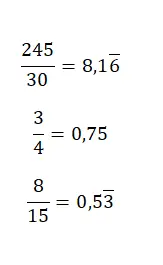
exercices de fractions
Maintenant que vous connaissez toute la théorie sur les fractions, nous vous recommandons de faire quelques exercices. De cette façon, vous apprendrez tous les concepts expliqués plus en profondeur et le jour de l’examen, vous irez plus vite en résolvant les calculs. De plus, vous aurez vu tous les types d’ exercices de fractions qui existent et vous saurez comment les résoudre en conséquence. Enfin, laissez-moi vous dire que nous avons également à votre disposition un calculateur de fractions en ligne, avec lequel vous pouvez résoudre toutes les opérations sur les fractions.