Fonctions polynomiales

Dans cet article, vous trouverez une explication très détaillée sur les fonctions polynomiales , qui est complétée par des exemples. De plus, vous pourrez voir comment les fonctions polynomiales sont utilisées dans la vie de tous les jours grâce aux exercices que nous vous présenterons à la fin.

Qu’est-ce qu’une fonction polynomiale ?

Les fonctions polynomiales ou fonctions polynomiales sont des fonctions qui sont données par une expression algébrique équivalente à un polynôme . Cela signifie que l’expression doit suivre la structure d’un polynôme : f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ , selon la structure dont on déterminera le type de fonction polynomiale que l’on va traiter. Une autre caractéristique très pertinente de ces fonctions est que tous leurs exposants des inconnues sont positifs et entiers .

Parties d’une fonction polynomiale

Nous pouvons souligner trois éléments importants concernant ces fonctions :

• Coefficients polynomiaux : ce sont les nombres qui accompagnent les inconnues, par exemple le 3 du terme suivant est un coefficient : 3x ² . Il faut noter qu’il y a autant de coefficients que de termes dans le polynôme.
• Exposants ou indices du polynôme : ce sont les puissances des inconnues, par exemple le 2 du terme suivant est un exposant : 3x ² . Et comme nous l’avons déjà expliqué, dans le cas d’une fonction polynomiale, ils seront toujours positifs et entiers.
• Degré du polynôme : cette valeur équivaut à l’exposant du degré le plus élevé parmi tous les termes qui composent le polynôme. Dans le cas du polynôme f(x) = 3x ² – 4x + 2, le degré est égal à deux.

Comment savoir si une fonction est polynomiale ou non ?

Pour identifier une fonction polynomiale, il faut regarder si elle répond aux caractéristiques dont nous venons de parler. Nous allons commencer par vérifier si l’expression qui définit la fonction a une structure polynomiale : f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ . Et puis, nous vérifierons que les indices sont positifs et entiers, avec ces étapes simples, nous pourrons déterminer si une fonction est polynomiale ou non.

Types de fonctions polynomiales avec exemples

Ensuite, nous vous montrerons les différents types de fonctions polynomiales qui existent, qui sont classées selon le degré du polynôme. De plus, vous trouverez un exemple de représentation graphique pour chaque type. Grâce à ces exemples de fonctions polynomiales vous pourrez mieux voir les différences entre les différentes catégories.

fonctions constantes

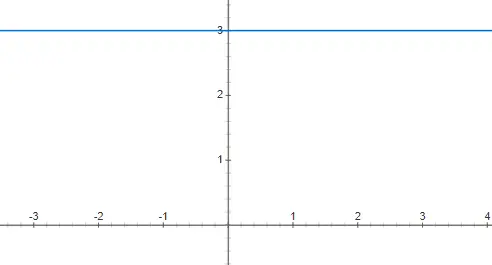
Les fonctions constantes sont équivalentes à un polynôme de degré 0, cela signifie que le coefficient de x est 0. C’est pourquoi les fonctions de ce type ne dépendent pas de la valeur de la variable indépendante x. Par conséquent, sa représentation graphique est une ligne horizontale, qui est infinie. Ci-dessous vous pouvez trouver représenté l’exemple f(x) = 3 :

fonctions polynomiales du premier degré

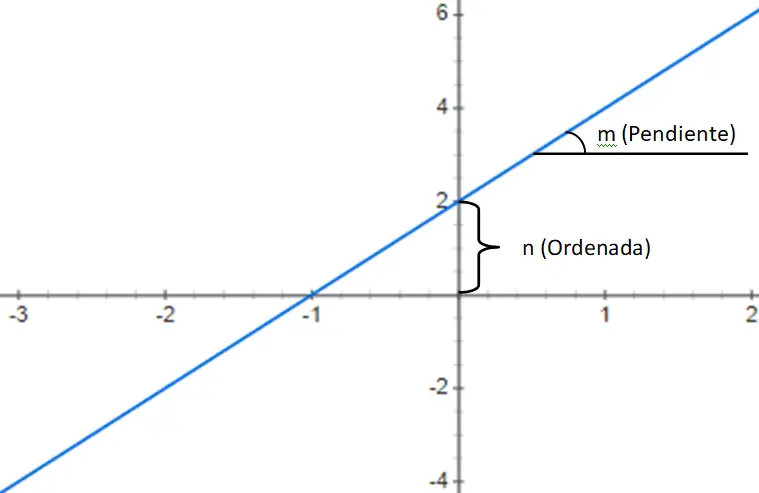
Deuxièmement, nous trouvons les fonctions polynomiales du premier degré , qui sont données par un polynôme de degré 1 avec la structure suivante : f(x) = mx + n. Cette expression est composée d’un nombre appelé pente (m) qui multiplie la variable xy par une constante (n) qui s’ajoute à ce produit. Ainsi, sur la base des valeurs de m et n, nous pouvons identifier trois types de fonctions différents :

• Fonctions affines : ce sous-type se caractérise par le fait d’avoir une valeur de n différente de 0, c’est-à-dire que la valeur de l’ordonnée est différente de 0. Par conséquent, ce type de fonction ne passe pas par le point (0, 0), également appelé origine. Commentez également que si m < 0, la fonction sera décroissante, tandis que si m > 0, la fonction sera croissante.
• Fonctions linéaires : la seule distinction que ces fonctions ont par rapport aux fonctions affines est que n = 0, elles n’ont donc pas d’ordonnée. Par conséquent, l’expression des fonctions linéaires est équivalente à f(x) = mx. Ce type est assez facile à représenter, puisqu’il passe toujours par le point (0, 0) et à partir de la pente on obtient déjà le graphe.
• Fonctions d’identité : ce dernier type est un sous-groupe de fonctions linéaires, qui a n = 0 et m = 1. Cela signifie que l’expression reste f(x) = x, avec laquelle la représentation graphique est une diagonale qui forme un angle de 45º avec l’un des axes. Ce type de fonction passe également par le point d’origine (0, 0).

Ci-dessous, vous trouverez un exemple de fonction polynomiale du premier degré, plus précisément une fonction affine f(x) = 3x + 2 :

fonctions quadratiques

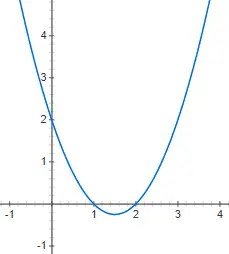
Les fonctions quadratiques ou fonctions du second degré s’expriment au moyen de polynômes du second degré, qui suivent la structure : f(x) = ax ² + bx + c, où a est différent de 0. Dans ce cas, la représentation graphique est beaucoup plus complexe, puisqu’il ne s’agit plus d’une droite, mais d’une parabole verticale . Ci-dessous, vous pouvez trouver la représentation de la fonction quadratique f(x) = 2x ² + 4x – 1 :

fonctions cubiques

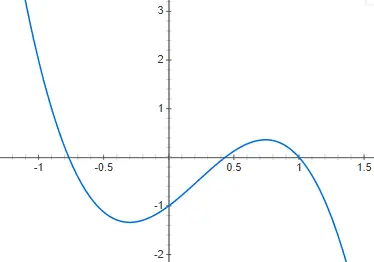
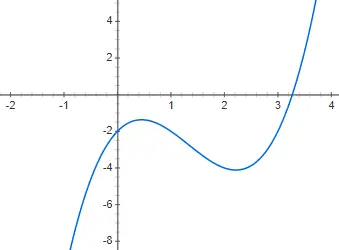
Les fonctions cubiques ou fonctions du troisième degré sont données par un polynôme de degré trois : f(x) = ax ³ + bx ² + cx + d, étant un différent de 0. La représentation d’une fonction de ce style est encore plus complexe que celle du second degré, puisqu’elle peut avoir plusieurs formes différentes. Bien que la forme de base, ou du moins la plus courante, soit celle que nous allons vous montrer dans l’exemple suivant, f(x) = 2x ³ – 4x ² + 2x – 2 :

Propriétés des fonctions polynomiales

Les fonctions polynomiales ont une série de propriétés ou de caractéristiques qui les distinguent des autres fonctions, et nous les détaillerons le plus clairement possible ci-dessous. De cette façon, lorsque vous verrez des fonctions de ce type, il vous sera très facile de les identifier :

• Le domaine d’une fonction polynomiale est égal à tous les nombres réels : Dom f = R ou Dom f = (-∞, ∞), ils sont donc continus sur tout l’ensemble des nombres réels.
• Son point d’intersection sur l’axe Y est équivalent à (0, a ₀ ), ₀ étant le terme indépendant.
• Coupe le long de l’axe X un nombre de fois égal ou inférieur au degré du polynôme.
• Les fonctions polynomiales n’ont pas d’asymptotes.
• Si l’exposant de tous les termes est impair, alors la représentation graphique est symétrique par rapport à l’origine de la coordonnée, tandis que si l’exposant de tous les termes est pair, elle est symétrique par rapport à l’axe OY.
• Le nombre de points d’inflexion d’une fonction de ce style est égal ou inférieur à n – 2, où n est le degré.
• Le nombre de maxima et de minima relatifs d’une fonction de ce style est égal ou inférieur à n – 1, où n est le degré.

Comment analyse-t-on une fonction polynomiale ?

Pour analyser une fonction polynomiale, nous devons suivre la même procédure que nous utiliserions pour analyser toute autre fonction. Dans la liste suivante nous avons résumé les différents éléments qui doivent être étudiés ou traités :

• Domaine et gamme
• Points d’intersection avec les axes horizontal et vertical
• Monotonie (croissante et décroissante, maxima et minima)
• Courbure (en fonctions de degré supérieur à un)

Évidemment, nous pouvons porter l’analyse à un autre niveau et étudier bien d’autres éléments, même si cela devrait suffire. Puisque, connaissant ces éléments, vous aurez une idée claire de ce à quoi ressemble la fonction et vous pourrez la représenter graphiquement.

Exercices sur les fonctions polynomiales

Ensuite, nous vous proposons une série d’exercices pour vous entraîner à représenter des fonctions , en particulier des fonctions polynomiales. De cette façon, vous consoliderez tous les concepts expliqués dans cet article :

Exercice 1

Représentez graphiquement la fonction polynomiale du premier degré suivante f(x) = x + 2 et dites de quel type il s’agit :

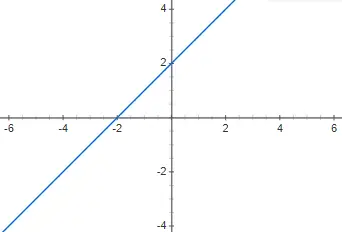
C’est une fonction polynomiale affine du premier degré, car elle a n différent de 0 et m différent de 0.

Exercice 2

Représenter graphiquement la fonction polynomiale du second degré suivante f(x) = x ² + x – 2 :

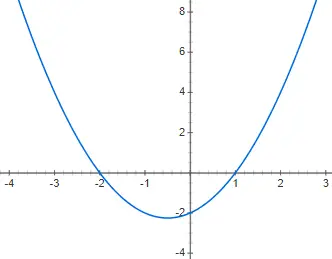
Exercice 3

Représenter graphiquement la fonction polynomiale du troisième degré suivante f(x) = x ² + x – 2 :