Il est très courant de représenter des fonctions pour pouvoir analyser graphiquement la relation entre les différentes variables qui composent cette fonction. Ou parfois, ces types de représentations sont même utilisés pour acheter plusieurs fonctionnalités. Ceci est particulièrement utilisé lors de la réalisation d’études statistiques. Cela étant dit, nous allons vous expliquer aujourd’hui une méthode très simple qui ne consiste qu’en 3 étapes pour pouvoir représenter graphiquement n’importe quelle fonction. De plus, nous discuterons également de la manière d’analyser le résultat graphique afin de tirer des conclusions.
Types de fonctions
Tout d’abord, nous devons comprendre les caractéristiques des différents types de fonctions et quelles sont les différences à prendre en compte lors de leur représentation. De cette façon, il nous sera plus facile d’effectuer la représentation graphique, c’est pourquoi nous allons maintenant commenter brièvement chaque type. Il convient de noter qu’il existe de nombreux types de fonctions, nous allons donc nous concentrer sur les deux types les plus importants de fonctions polynomiales et sur les fonctions par morceaux.
fonctions linéaires
La fonction linéaire ou fonction polynomiale du premier degré est la fonction dont l’expression est un polynôme de degré 1. Ensuite, son expression suit le modèle f(x) = mx + n , où m est la pente et n est l’ordonnée. Fondamentalement, ces fonctions ont une forme graphique équivalente à une ligne. Ci-dessous, vous pouvez voir un exemple :
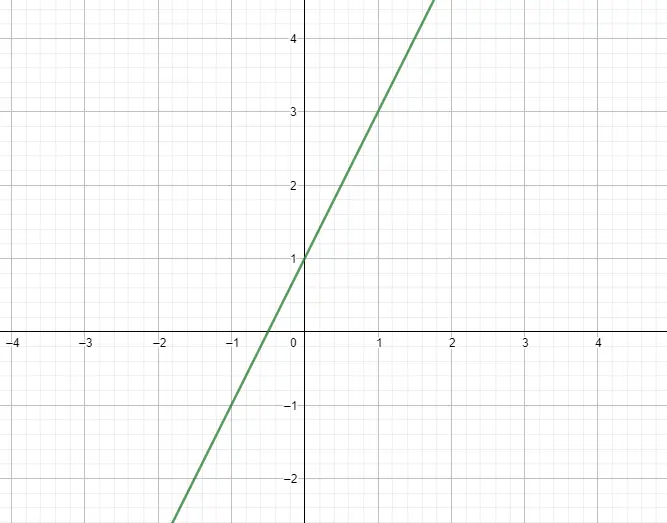
fonctions quadratiques
La fonction quadratique ou fonction parabolique s’exprime au moyen d’un polynôme du second degré et c’est pourquoi elle a une forme de parabole. Comme modèle à suivre nous prendrons en compte l’expression suivante : f(x) = ax² + bx + c, où a ≠ 0. Aussi, il y a deux autres caractéristiques notables de ces fonctions, l’amplitude et la croissance. Ci-dessous, vous pouvez voir un exemple :
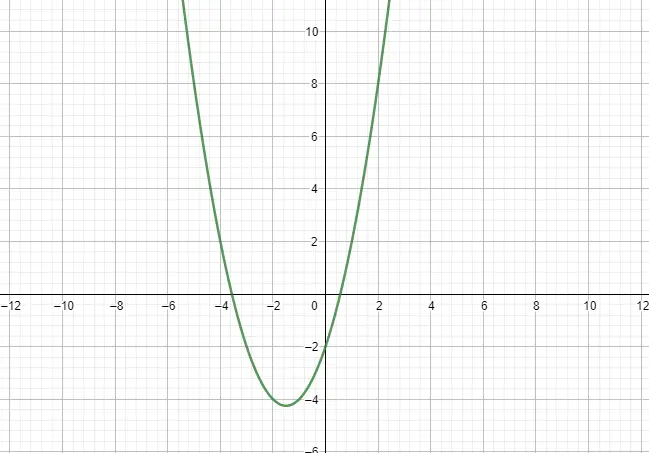
Fonctions par morceaux
Une fonction définie par morceaux est une fonction qui a des définitions différentes selon la valeur de x. Ainsi, lorsque x occupe une certaine plage de valeurs, nous devons essayer une expression. Alors que lorsque le x occupe d’autres valeurs, il faut traiter une expression différente. C’est ici que l’on trouve des discontinuités et donc des limites. Puisque, là où une fonction se termine, une autre peut commencer, mais sans se connecter directement. Ci-dessous, vous pouvez voir un exemple :
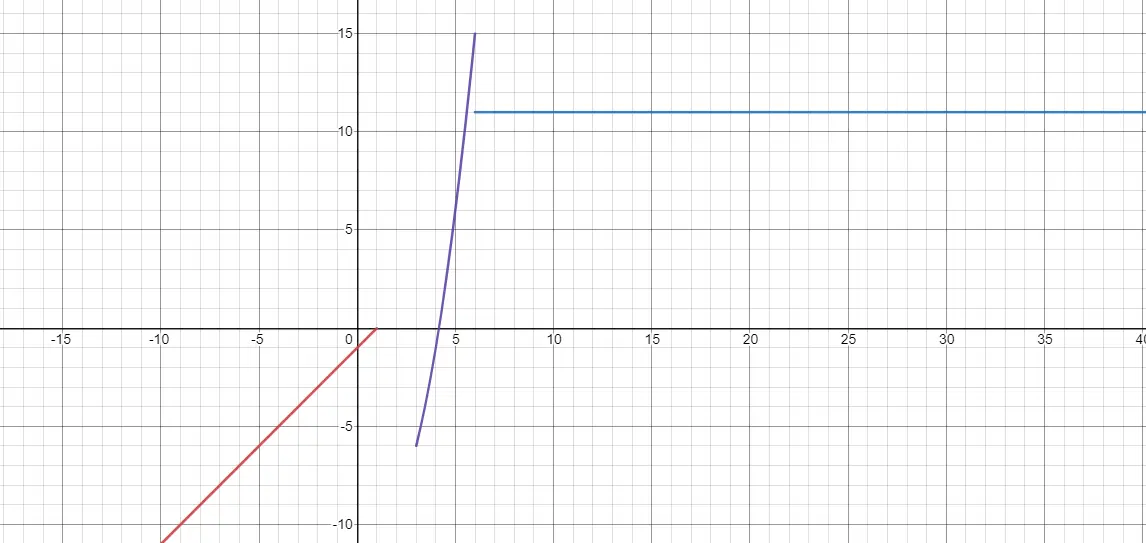
Comment représenter des fonctions linéaires ?
Afin de représenter graphiquement une fonction linéaire, nous devons suivre trois étapes très simples. Ensuite, nous expliquerons la procédure, bien que si vous voulez apprendre à représenter graphiquement des fonctions paraboliques, nous vous recommandons de consulter la section suivante.
Créer un tableau de valeurs
Pour pouvoir représenter graphiquement une fonction, nous devons créer un tableau de valeurs dans lequel nous écrirons toutes les valeurs des variables. Fondamentalement, cela nous permettra d’établir une relation entre les deux variables et de cette manière, nous pourrons tracer le chemin de la fonction. Si vous ne savez pas comment faire un tableau de valeurs, vous pouvez regarder ce dernier lien. Bien qu’en résumé, il consiste à donner une valeur à la variable indépendante et à substituer l’inconnue dans la fonction qui les relie. Ainsi nous aurons les deux numéros associés, le tableau suivant montre un exemple :
A partir de la fonction f(x) = 2x+1 :
| X | f(x) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
Dessinez des points sur le graphique et joignez-les en dessinant la fonction
Une fois que nous avons fait le tableau, nous pouvons commencer à dessiner les points sur un graphique. Nous le faisons en associant la variable indépendante à l’axe x et l’autre à l’axe y, et de cette façon nous obtiendrons les points. Vous pouvez dessiner autant de points que vous le souhaitez, bien que pour représenter des fonctions de ce style, il suffit généralement de calculer cinq points. Depuis, ils suivent une trajectoire rectiligne et, par conséquent, elle continue d’être la même peu importe à quel point vous avancez.
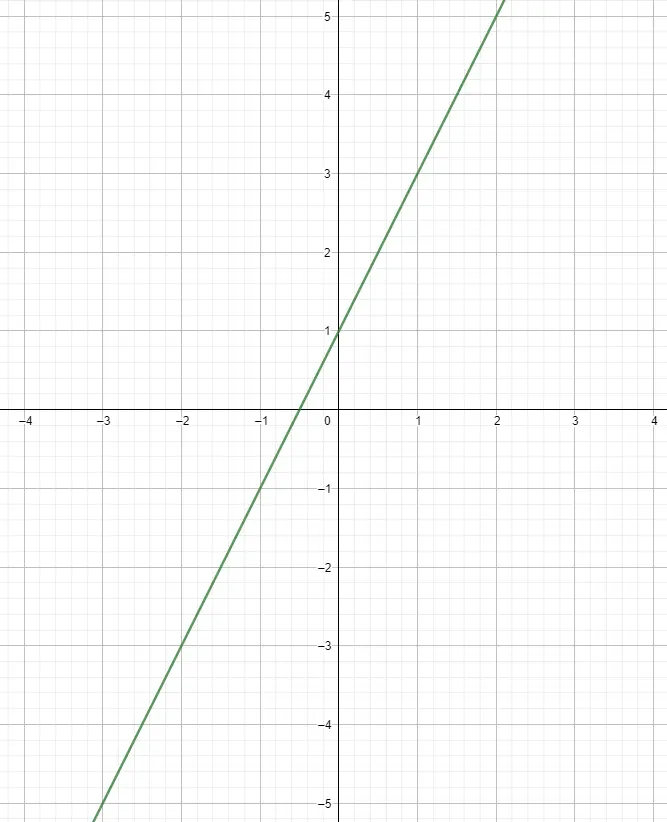
Utilisation de la pente pour représenter graphiquement une fonction linéaire
Il existe une deuxième méthode pour pouvoir représenter graphiquement des fonctions linéaires sans tableaux de valeurs, qui consiste à calculer la pente de la fonction : m = (variation verticale / variation horizontale). Donc, une fois que nous avons calculé la pente, nous devons regarder le point de départ. En reprenant l’exemple précédent f(x) = 2x+1, on sait que le point de départ sera (0, 1), car à x = 0, l’ordonnée = 1 (on la déduit du +1 dans l’expression). Et puis il suffit d’ajouter la pente, qui dans ce cas est égale à +2 verticales pour 1 horizontale. Ensuite, nous saurons que le point suivant sera (1,3).
Comment représenter des fonctions quadratiques ?
Pour représenter une fonction quadratique, nous pouvons suivre deux méthodes, la première passe par des tables de valeurs. Et la seconde consiste à calculer une série de points clés : le sommet, les points d’intersection avec l’axe X et le point d’intersection avec l’axe Y. Ce dernier est celui que nous expliquerons ci-dessous :
Calculer le sommet d’une parabole
Il existe deux formules qui nous permettent de calculer le sommet d’une fonction parabolique, essentiellement l’une nous donne le point de sommet de l’axe X et l’autre nous donne le point de sommet de l’axe Y. Vous pouvez trouver les deux formules ci-dessous, mais les deux ont une structure similaire.
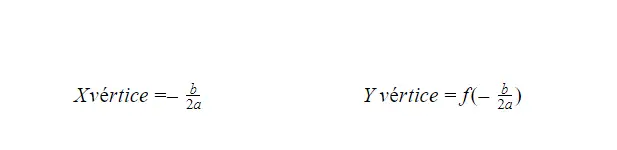
Calculer les points d’intersection avec l’axe X d’une fonction quadratique
Pour obtenir les points d’intersection de l’axe X (les points de la parabole qui sont situés sur l’axe des abscisses), il suffit d’égaliser l’expression à 0 : f(x) = 0. Ensuite, il ne nous restera plus qu’à résoudre l’équation et nous aurons déjà les valeurs de X que nous recherchons. Il convient de noter qu’étant une fonction quadratique, nous obtiendrons deux résultats, pas un seul.
Calculer le point d’intersection avec l’axe Y d’une fonction quadratique
Enfin, pour obtenir le point d’intersection avec l’axe Y, il suffit de calculer c = f(0). Et puisqu’une parabole coupe toujours l’axe vertical (des ordonnées) lorsque x = 0, alors on dira que le point de coupure de l’axe Y sera (0,c). Une fois que nous aurons tous ces points, nous pourrons les dessiner sur le graphique et nous n’aurons plus qu’à les joindre en dessinant la parabole comme ceci.
Comment représenter des fonctions par morceaux ?
Pour pouvoir représenter des fonctions en morceaux, vous pouvez mélanger toutes les méthodes que nous avons expliquées précédemment. Puisque les fonctions de ce style sont composées de tous les types de fonctions dont nous avons parlé. Par conséquent, il y en aura que vous devrez calculer à travers un tableau de valeurs et d’autres que vous devrez calculer avec d’autres méthodes. Cependant, une fois que vous maîtriserez ceux que nous avons expliqués dans cet article, vous n’aurez plus aucun problème lors de la représentation de fonctions en morceaux.
D’autre part, puisque lors de leur représentation, vous devez faire une étude de continuité, nous vous recommandons d’apprendre à résoudre les limites , si vous ne savez pas déjà comment. Cela vous aidera à représenter correctement les points de terminaison de chaque fonction. Cela étant dit, vous serez maintenant prêt à représenter graphiquement des fonctions par morceaux et tout autre type de fonction également. Nous vous laissons maintenant avec une série d’astuces graphiques et avec une explication très utile sur la capacité de la calculatrice à créer des graphiques.
Comment faire des graphiques avec la calculatrice ?
Si vous avez unecalculatrice graphique , elle aura la capacité de représenter graphiquement. Ce qui peut être très facile à faire une fois que vous connaissez la procédure, mais si vous ne savez toujours pas comment faire, maintenant nous allons vous l’expliquer.
- Accéder au mode graphique : la première étape consiste à accéder à l’option graphiques ou représentations graphiques à partir du menu. Cette option peut être étiquetée avec un nom différent pour votre calculatrice, mais elle contiendra des mots similaires à la représentation graphique ou à ceux dont nous avons déjà parlé.
- Personnalisez les options du graphique : une fois que nous sommes dans l’éditeur de graphique, nous devons donner un nom au fichier, étiqueter les axes, sélectionner le nombre d’éléments qui seront représentés graphiquement et configurer les options esthétiques de la représentation. C’est une étape très rapide à faire.
- Additionnez les points de la fonction : vous pouvez alors commencer à additionner les points qui formeront la figure. Vous pouvez le faire en écrivant les points avec la notation suivante : (0,1), (3,2)… Et vous continuerez à ajouter les points jusqu’à ce que vous ayez terminé la représentation graphique.
- Utilisez la fonction « Aperçu » : une fois que vous avez terminé le projet, vous pouvez prévisualiser le résultat et voir s’il se déroule comme prévu. De plus, de nombreux modèles ont des options d’édition avec cet aperçu, vous pouvez donc modifier le résultat jusqu’à ce qu’il soit parfait.
- Enregistrez le projet : une fois que toute la procédure d’édition est terminée, n’oubliez pas de l’enregistrer dans un emplacement facile à mémoriser. De cette façon, chaque fois que vous en avez besoin, vous pouvez accéder à nouveau au projet pour le visualiser ou pour apporter les améliorations que vous souhaitez.
Meilleures calculatrices pour représenter les fonctions
Si vous êtes intéressé par l’acquisition d’un modèle graphique pour pouvoir représenter des fonctions sur une même calculatrice, nous vous conseillons deux modèles : le HP 50G et le HP Prime . Ce sont deux modèles de la plus haute qualité, bien qu’ils soient chers, vous devez donc vous demander si l’investissement est rentable pour vous. Par exemple, si vous allez étudier une carrière comme l’ingénierie qui est très complexe en termes de mathématiques, alors il sera fortement recommandé d’acheter l’un de ces deux modèles. Mais, si vous n’avez pas besoin d’autant de puissance de calcul ou de représentation graphique, peut-être que le Casio FX-9750GII vous suffira.
Comment représenter graphiquement des fonctions en ligne ?
Vous pouvez toujours choisir l’option d’utiliser des programmes graphiques en ligne, tels que : Desmos , Geogebra et bien d’autres. De cette façon, vous obtiendrez des graphiques très précis de manière rapide. On peut dire que la forme numérique est utilisée lorsque vous souhaitez représenter graphiquement des fonctions facilement et rapidement. En revanche, si vous souhaitez représenter graphiquement des fonctions afin de pouvoir les éditer (modifier tous leurs attributs) et disposer de ressources d’analyse de fonctions de haute qualité à portée de main, nous vous recommandons alors d’acheter une calculatrice scientifique.