▷ Comment trouver la fonction inverse ou réciproque (exercices résolus)

Dans cet article, nous expliquons ce qu’est une fonction inverse (ou réciproque) et comment calculer l’inverse d’une fonction. Vous découvrirez également comment savoir facilement si une fonction a un inverse ou non et les propriétés de ce type de fonctions. Enfin, vous pouvez vous entraîner avec des exercices pas à pas sur les fonctions inverses.

Quelle est la fonction inverse ?

La fonction inverse, également appelée fonction réciproque, est la fonction dont le domaine est la plage d’une autre fonction (la fonction d’origine) et dont la plage est le domaine de la fonction d’origine. La fonction inverse de la fonction f est exprimée avec le symbole f ^-1 .

Par conséquent, la fonction inverse de f(x) est la fonction qui satisfait la condition suivante :

Où

$f^{-1}$ est la fonction inverse de $f.$

Le concept de fonction inverse peut également être défini à l’aide de la composition de fonctions, puisque toute fonction composée avec sa fonction inverse est égale à la fonction identité :

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

➤ Voir : qu’est-ce que la composition des fonctions ?

Donc si l’équation précédente est remplie, cela signifie que

$f^{-1}$ est la fonction inverse (ou fonction réciproque) de $f.$

Exemple de fonction inverse

Étant donné la définition de la fonction inverse, résolvons un exemple pour mieux comprendre sa signification.

Déterminez si les fonctions suivantes sont inverses les unes des autres :

$f(x)=2x+1\qquad g(x)=\cfrac{x-1}{2}$

Si les deux fonctions sont inverses l’une de l’autre, les 2 conditions suivantes seront remplies :

$(f \circ g)(x) = x \qquad \qquad (g \circ f)(x) = x$

Vérifions donc si les deux équations sont satisfaites. Nous vérifions d’abord

$(f \circ g)(x) = x:$

$\begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}$

➤ Si vous ne comprenez pas le calcul que nous venons de faire, vous devez vous rendre sur le lien ci-dessus pour Quelle est la composition des fonctions ? , nous y expliquons comment résoudre ce type d’opération avec des fonctions.

De sorte que

$(f \circ g)(x) = x$ oui, c’est accompli.

Vérifions maintenant l’égalité

$(g \circ f)(x) = x :$

$\begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}$

Et la condition d’inversibilité

$(g \circ f)(x) = x$ il est également accompli.

En conclusion, comme les deux équations sont vérifiées, les deux fonctions sont inverses l’une de l’autre.

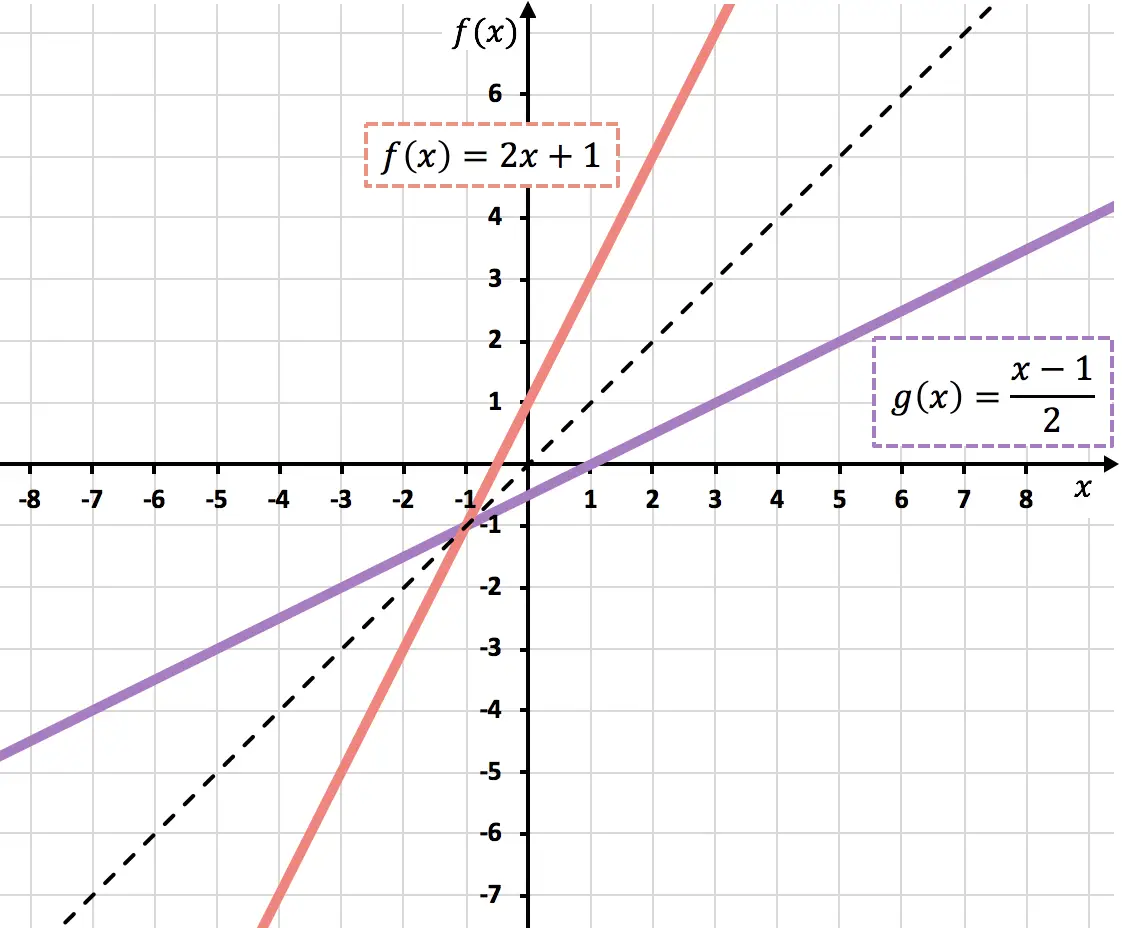
Ci-dessous, vous pouvez voir les deux fonctions représentées graphiquement. Notez que les graphiques de deux fonctions inverses sont symétriques par rapport à la bissectrice des premier et troisième quadrants :

Comment savoir si une fonction a un inverse

Une fonction a une fonction inverse si c’est une fonction injective , c’est-à-dire si chaque valeur de l’ensemble de son domaine correspond à une seule valeur de son intervalle.

Fonction exponentielle avec fonction inverse

Fonction quadratique sans fonction inverse

Par exemple, la fonction exponentielle de gauche a une fonction inverse car chaque x correspond à une seule valeur de f(x) . En revanche, la fonction quadratique de droite n’a pas de fonction inverse puisqu’elle a plusieurs valeurs de x dont les images sont égales (par exemple f(1)=f(3)=2) .

De même, une fonction bijective consiste en une fonction qui est à la fois injective et surjective, par conséquent, toute fonction bijective a également une fonction inverse.

D’un autre côté, vous devez garder à l’esprit que la fonction inverse n’est pas la même chose que l’ inverse multiplicatif d’une fonction , mais plutôt deux concepts différents. Pour trouver l’inverse multiplicatif d’une fonction, il suffit de calculer 1 correspondance par ladite fonction.

$f^{-1}(x) \neq \cfrac{1}{f(x)}$

Dans la section suivante, nous verrons comment déterminer la fonction inverse.

Comment trouver la fonction inverse

Pour calculer la fonction inverse d’une fonction, les étapes suivantes doivent être effectuées :

Remplacez f(x) par y .
Changez tout x en y , et vice versa.
Effacez la variable y .
Remplacez la variable y par f ^-1 (x) . La fonction inverse est l’expression trouvée pour f ^-1 (x) .

Afin que vous puissiez voir exactement comment la fonction inverse est calculée, nous allons déterminer l’inverse de la fonction suivante à titre d’exemple :

$f(x) =4x+5$

Tout d’abord, nous devons remplacer

$f(x)$ pour $y$ :

$y=4x+5$

Maintenant, nous changeons tout

$x$ de la fonction par $y$ , et vice versa:

$y= 4x+5 \quad \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \quad x= 4y+5$

Ensuite, nous effaçons la variable

$y:$

$x=4y+5$

$x-5=4y$

$\cfrac{x-5}{4}=y$

$y=\cfrac{x-5}{4}$

Et enfin, la fonction inverse de

$f(x)$ est l’expression algébrique que nous avons obtenue en isolant $y:$

$\bm{f^{-1}(x) = } \cfrac{\bm{x-5}}{\bm{4}}$

Exercices résolus de la fonction inverse

Ci-dessous, nous avons préparé plusieurs exercices étape par étape sur la fonction inverse afin que vous puissiez vous entraîner.

N’oubliez pas que si vous ne comprenez pas la résolution d’un exercice ou souhaitez que nous résolvions un problème à votre place, vous pouvez nous écrire dans les commentaires !

Exercice 1

Vérifiez si les deux fonctions suivantes sont inverses (ou réciproques) ou non :

$f(x)=3x-7\qquad g(x)=\cfrac{x+7}{3}$

Voir la solution

Pour que les deux fonctions soient inverses l’une de l’autre, il faut que ce qui suit soit vrai :

$(f \circ g)(x)=x \qquad \qquad (g \circ f)(x)=x$

Il faut donc vérifier si les deux conditions sont remplies. Nous vérifions d’abord

$(f \circ g)(x)=x :$

$\begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}$

Pourtant,

$(f \circ g)(x) = x$ oui, c’est accompli.

Vérifions maintenant l’autre composition de fonctions

$(g \circ f)(x)=x :$

$\begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}$

De manière que

$(g \circ f)(x) = x$ il est également accompli.

Comment se réalise-t-il que

$(f \circ g)(x)=x$ et que $(g \circ f)(x)=x$ , les deux fonctions sont inverses l’une de l’autre.

Exercice 2

Calculez l’inverse (ou fonction réciproque) de la fonction polynomiale du premier degré suivante :

$f(x)=-2x-3$

Voir la solution

La première chose à faire pour inverser la fonction est de substituer le terme

$f(x)$ pour $}y:$

$y=-2x-3$

Maintenant, nous changeons le

$x$ par $y$ , et vice versa:

$y=-2x-3 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =-2y-3$

Et puis nous dégageons

$y:$

$x =-2y-3$

$x +3=-2y$

$\cfrac{x +3}{-2}=y$

$y = \cfrac{x +3}{-2}$

Nous avons déjà réussi à dégager

$y$ . Par conséquent, la fonction inverse de $f(x)$ est:

$\bm{f^{-1}(x) = -} \cfrac{\bm{x+3}}{\bm{2}}$

Exercice 3

Inversez la fonction polynomiale du deuxième degré suivante :

$f(x)=x^2-1$

Voir la solution

Pour trouver la fonction inverse nous suivrons la procédure que nous avons vue ci-dessus. Alors nous appellerons

$y$ à la fonction $f(x):$

$y=x^2-1$

Deuxièmement, nous modifions le

$x$ pour la $y$ , et vice versa:

$y=x^2-1 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =y^2-1$

Et enfin, on isole la variable

$y:$

$x =y^2-1$

$x+1=y^2$

$\sqrt{x+1}=y$

$y=\pm \sqrt{x+1}$

Cependant, dans ce cas la fonction obtenue possède deux images pour chaque élément de son domaine (l’image positive et l’image négative). Par conséquent, il n’existe pas de fonction inverse de la fonction problème.

Exercice 4

Déterminer la fonction inverse (ou fonction réciproque) de la fonction rationnelle suivante :

$\displaystyle f(x)=\frac{x-1}{2x+3}$

Voir la solution

Tout d’abord, nous remplaçons

$f(x)$ pour $y:$

$y=\cfrac{x-1}{2x+3}$

Maintenant, nous changeons le

$x$ du numérateur et du dénominateur $y$ , et vice versa:

$y=\cfrac{x-1}{2x+3} \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x=\cfrac{y-1}{2y+3}$

Et puis nous dégageons

$y:$

$x=\cfrac{y-1}{2y+3}$

L’expression

$2y +3$ divise tout le côté droit de l’équation, nous pouvons donc le multiplier en multipliant tout le côté gauche de l’équation :

$x\cdot (2y+3)=y-1$

$2yx+3x=y-1$

Nous mettons tous les termes avec

$y$ d’un côté de l’équation, et les autres termes de l’autre côté :

$2yx-y=-3x-1$

Afin de dégager

$}y$ , nous extrayons le facteur commun du côté gauche de l’équation :

$y(2x-1)=-3x-1$

Et comme facteur

$(2x-1)$ consiste à multiplier tout le côté gauche de l’équation, nous pouvons le faire en divisant tout le côté droit :

$y=\cfrac{-3x-1}{2x-1}$

Nous avons déjà réussi à dégager

$y$ . Donc la fonction réciproque de $f(x)$ est:

$\bm{f^{-1}(x)=} \cfrac{\bm{-3x-1}}{\bm{2x-1}}$

Propriétés de la fonction inverse

La fonction inverse a les caractéristiques suivantes :

La fonction inverse est unique, c’est-à-dire que si une fonction est inversible, pour cette fonction il n’y a qu’une seule fonction inverse.

Le domaine de la fonction inverse est la plage (ou plage) de la fonction d’origine.

De même, le parcours de la fonction inverse est équivalent au domaine de la fonction d’origine.

Toute fonction composée de sa fonction inverse donne la fonction d’identité (x).

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

La représentation graphique d’une fonction et la représentation graphique de sa fonction inverse sont symétriques par rapport à la bissectrice des premier et troisième quadrants.

L’inverse de la fonction inverse est égal à la fonction d’origine :

$\left(f^{-1}\right)^{-1}=f$

Inverser une fonction composite équivaut à calculer l’inverse de chaque fonction séparément puis à composer les fonctions inverses.

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Une fonction est simultanément continue avec sa fonction inverse, ou en d’autres termes, si une fonction est continue, sa fonction inverse le sera aussi.

Si une fonction est différentiable et que la dérivée ne disparaît à aucun moment 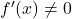$f'(x)\neq 0$ , sa fonction inverse sera également dérivable.

De plus, la dérivée de la fonction inverse peut être calculée en appliquant le théorème de la fonction inverse , dont la formule est :

$\left(f^{-1}\right)'(y)=\cfrac{1}{f'(x)}$

Fonction inverse (ou réciproque)

Quelle est la fonction inverse ?

Exemple de fonction inverse

Comment savoir si une fonction a un inverse

Comment trouver la fonction inverse

Exercices résolus de la fonction inverse

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Propriétés de la fonction inverse

Leave a Comment Cancel Reply