▷ Concavité et convexité d'une fonction (courbure)

Vous découvrirez ici ce que sont la concavité et la convexité d’une fonction et comment savoir si une fonction est concave ou convexe. De plus, vous pourrez vous entraîner avec des exercices résolus étape par étape sur la courbure d’une fonction.

Quelle est la concavité et la convexité d’une fonction ?

La concavité et la convexité d’une fonction font référence à la courbure du graphique d’une fonction. Une fonction concave est une fonction dont le graphique a la forme d’une montagne, et une fonction convexe est une fonction dont le graphique a la forme d’une vallée.

Dans le paragraphe précédent, les fonctions concaves et convexes ont été définies de manière informelle pour faciliter la compréhension, mais la définition mathématique de la fonction concave et de la fonction convexe est la suivante :

Fonction concave : lorsque le segment qui joint deux points quelconques de la fonction est en dessous de la courbe.
Fonction convexe : lorsque le segment qui joint deux points quelconques de la fonction est au-dessus de la courbe.

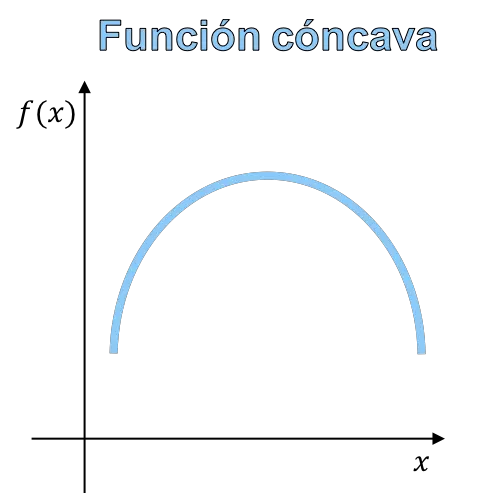
En fin de compte, la différence entre une fonction concave et une fonction convexe réside dans la forme de la fonction et, par conséquent, vous pouvez distinguer la concavité de la convexité à partir du graphique de la fonction.

Cependant, une fonction ne doit pas nécessairement être concave ou convexe sur tout son domaine, mais peut également être concave sur un intervalle et convexe sur un autre intervalle.

Remarque : La communauté mathématique n’est toujours pas entièrement d’accord et, par conséquent, certains professeurs disent le contraire : ils appellent une fonction concave celle qui a la forme d’un

$\bm{\cup}$ , et une fonction convexe qui a la forme de $\bm{\cap}$ . Dans tous les cas, l’important est de savoir quelle est la fonction, quel que soit son nom.

Comment étudier la courbure d’une fonction

Étudier la courbure d’une fonction consiste à trouver la concavité et la convexité de la fonction, c’est-à-dire connaître les intervalles dans lesquels la fonction est concave et les intervalles dans lesquels la fonction est convexe.

Ainsi, pour étudier la courbure d’une fonction, les étapes suivantes doivent être effectuées :

Trouvez les points qui n’appartiennent pas au domaine de la fonction.
Calculez la dérivée première et la dérivée seconde de la fonction.
Trouver les racines de la dérivée seconde , c’est-à-dire calculer les points qui annulent la dérivée seconde en résolvant $f''(x)=0$ .
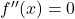Faites des intervalles avec les racines de la dérivée et les points qui n’appartiennent pas au domaine de la fonction.
Calculez la valeur de la dérivée seconde en un point de chaque intervalle.
Ainsi, le signe de la dérivée seconde détermine la concavité ou la convexité de la fonction dans cet intervalle :
- Si la dérivée seconde de la fonction est positive, la fonction est convexe sur cet intervalle.
- Si la dérivée seconde de la fonction est négative, la fonction est concave sur cet intervalle.

Exemple de comment trouver la courbure d’une fonction

Ensuite, nous allons résoudre un exemple étape par étape afin que vous puissiez voir comment les intervalles de concavité et de convexité d’une fonction sont calculés.

Étudiez la concavité et la convexité de la fonction suivante :

$f(x)=x^3-3x$

La première chose à faire est de calculer le domaine de définition de la fonction. Dans ce cas, nous avons une fonction polynomiale, donc le domaine de la fonction est constitué de nombres réels :

$\text{Dom } f= \mathbb{R}$

Une fois que nous avons calculé le domaine de la fonction, nous devons étudier à quels points la dérivée seconde de la fonction s’annule.

On calcule donc la dérivée première de la fonction :

$f(x)=x^3-3x \ \longrightarrow \ f'(x)= 3x^2-3$

On trouve ensuite la dérivée seconde de la fonction :

$f'(x)=3x^2-3 \ \longrightarrow \ f''(x)= 6x$

Et maintenant, nous fixons la dérivée seconde égale à 0 et résolvons l’équation :

$f''(x)=0$

$6x=0$

$x=\cfrac{0}{6}$

$x=0$

Une fois que nous avons calculé le domaine de la fonction et

$f''(x)=0$ , nous représentons tous les points critiques trouvés sur la ligne. Dans ce cas nous n’avons trouvé aucun point critique dans le calcul du domaine de définition de la fonction, mais nous avons obtenu un point qui annule la dérivée seconde de la fonction :

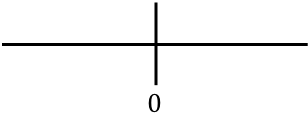
Et maintenant nous évaluons le signe de la dérivée seconde dans chaque intervalle, pour savoir si la fonction est concave ou convexe. Nous prenons donc un point dans chaque intervalle (jamais les points critiques) et regardons quel signe la dérivée seconde a à ce point :

$f''(x)=6x$

$f''(-1) = 6\cdot (-1)=-6 \ \rightarrow \ \bm{-}$

$f''(1) = 6\cdot 1=+6 \ \rightarrow \ \bm{+}$

Enfin, on en déduit les intervalles de concavité et de convexité de la fonction. Si la dérivée seconde est positive, cela signifie que la fonction est convexe.

$(\bm{\cup})$ , et si la dérivée seconde est négative cela signifie que la fonction est concave $(\bm{\cap})$ . Ainsi les intervalles de concavité et de convexité de la fonction sont :

Convexe

$(\bm{\cup})$ : $\bm{(0,+\infty)}$

Concave

$(\bm{\cap})$ : $\bm{(-\infty,0)}$

Exercices résolus sur la concavité et la convexité d’une fonction

Exercice 1

Calculez les intervalles de concavité et de convexité de la fonction polynomiale suivante :

$f(x) = x^3-3x^2-2x$

Voir la solution

La fonction dans l’exercice est un polynôme, donc le domaine de la fonction est constitué de nombres réels :

$\text{Dom } f= \mathbb{R}$

Après avoir déterminé le domaine de la fonction, on le différencie :

$f(x)=x^3-3x^2-2x \ \longrightarrow \ f'(x)= 3x^2-6x-2$

On trouve ensuite la dérivée seconde de la fonction :

$f'(x)= 3x^2-6x-2 \ \longrightarrow \ f''(x)= 6x-6$

Et maintenant, nous fixons la dérivée seconde égale à 0 et résolvons l’équation :

$f''(x)= 0$

$6x-6= 0$

$6x= 6$

$x= \cfrac{6}{6}$

$x=1$

Une fois que nous avons calculé le domaine de la fonction et résolu

$f''(x)=0$ , nous représentons tous les points singuliers trouvés sur la droite numérique :

Et maintenant, prenons un point appartenant à chaque intervalle et regardons quel signe a la dérivée seconde à ce point :

$f''(0)= 6\cdot 0-6 = -6 \ \rightarrow \ \bm{-}$

$f''(2)= 6\cdot 2-6 = 12-6=+6 \ \rightarrow \ \bm{+}$

Lorsque la dérivée seconde est supérieure à zéro, cela signifie que la fonction est convexe.

$(\bm{\cup})$ , mais lorsque la dérivée seconde est négative cela implique que la fonction est concave $(\bm{\cap})$ . Par conséquent, les intervalles de concavité et de convexité sont :

Convexe

$(\bm{\cup})$ : $\bm{(1,+\infty)}$

Concave

$(\bm{\cap})$ : $\bm{(-\infty,1)}$

Exercice 2

Étudiez la courbure de la fonction rationnelle suivante :

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Voir la solution

Nous devons d’abord calculer le domaine de la fonction. Puisqu’il s’agit d’une fonction rationnelle, nous mettons le dénominateur égal à zéro pour voir quels nombres n’appartiennent pas au domaine de la fonction :

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Cela signifie que lorsque x vaut -2 ou +2, le dénominateur sera 0. Et par conséquent, la fonction n’existera pas. Le domaine de la fonction est donc composé de tous les nombres sauf x=-2 et x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Deuxièmement, nous calculons la dérivée première de la fonction :

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Et puis on résout la dérivée seconde :

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Tous les termes sont multipliés par

$(x^2-4)$ . On peut donc simplifier la fraction :

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Calculons maintenant les racines de la dérivée seconde de la fonction :

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

Le terme

$\left(x^2-4\right)^3$ Il s’agit de diviser tout le côté gauche, nous pouvons donc le multiplier par tout le côté droit :

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

On extrait le facteur commun :

$x(8x^2+96)=0$

Pour que la multiplication soit égale à 0, il faut qu’un des deux éléments de la multiplication soit nul. Par conséquent, nous fixons chaque facteur égal à 0 :

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$ Il n’y a pas de solution puisqu’il n’existe pas de racine négative d’un nombre réel.

Nous représentons maintenant sur la ligne tous les points critiques obtenus, c’est-à-dire les points qui n’appartiennent pas au domaine (x=-2 et x=+2) et ceux qui annulent la dérivée seconde (x=0) :

Et on évalue le signe de la dérivée seconde dans chaque intervalle, pour savoir si la fonction est concave ou convexe. Nous prenons donc un point dans chaque intervalle et regardons quel signe a la dérivée seconde à ce point :

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Si la dérivée seconde est positive, cela signifie que la fonction est convexe.

$(\bm{\cup})$ , et si la dérivée seconde est négative cela signifie que la fonction est concave $(\bm{\cap})$ . Les intervalles de concavité et de convexité sont donc :

Convexe

$(\bm{\cup})$ : $\bm{(-2,0)\cup (2,+\infty)}$

Concave

$(\bm{\cap})$ : $\bm{(-\infty,-2)\cup (0,2)}$

Exercice 3

Une fonction

$f(x)$ a un extrême relatif dans $x=3$ . Et de plus, la fonction est convexe $(\cup )$ à ce même point. Déterminez si l’extrême relatif est un minimum ou un maximum.