Dérivée de l’arccotangente

Vous trouverez ici la formule de la dérivée de l’arccotangente et nous expliquerons comment dériver l’arccotangente d’une fonction avec des exemples.

Formule dérivée arccotangente

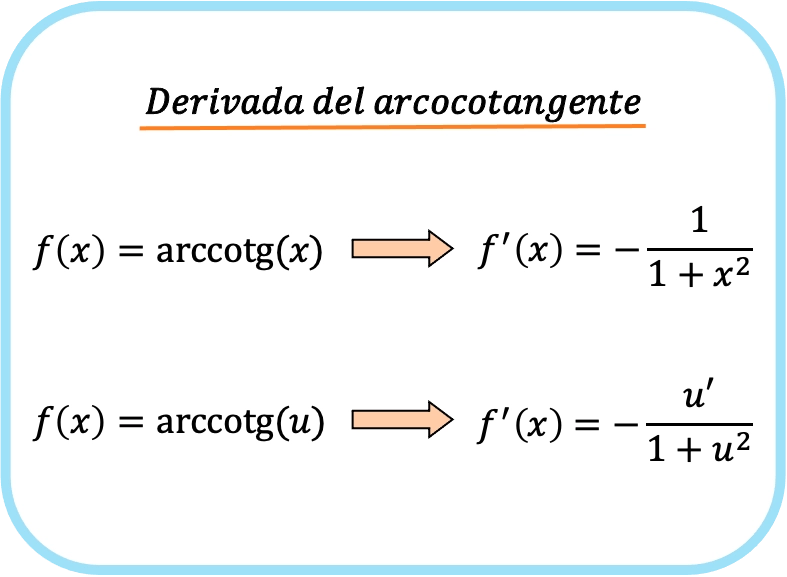
La dérivée de l’arc tangente de x est moins un divisé par un plus x au carré.

Par conséquent, la dérivée de l’arccotangente d’une fonction est égale à moins la dérivée de cette fonction divisée par un plus la fonction au carré.

Notez que les première et deuxième formules sont les mêmes, la seule différence est que la règle de chaîne est appliquée à la deuxième expression. En fait, si vous substituez un x à u, vous obtiendrez la première formule puisque la dérivée de la fonction x est 1.

Bien que l’arccotangente soit la fonction inverse de la cotangente, leurs dérivées sont assez différentes. En fait, la cotangente d’une fonction a trois façons d’être dérivée, vous pouvez toutes les voir ici :

➤ Voir : formule de la dérivée de la cotangente

Exemples de dérivée de l’arccotangente

Après avoir vu quelle est la formule de la dérivée de l’arccotangente, voici deux exercices résolus de ce type de dérivée trigonométrique. N’oubliez pas non plus que si vous avez des questions, vous pouvez laisser votre question ci-dessous dans les commentaires.

Exemple 1

Dans cet exemple, nous verrons de combien est la dérivée de l’arccotangente de la fonction quadratique x ² .

Dans l’argument de l’arccotangente, nous avons une fonction autre que x, nous devons donc appliquer la formule de la dérivée de l’arccotangente avec la règle de la chaîne :

La dérivée de x élevée à deux est 2x, donc au numérateur il faut mettre 2x et au dénominateur la fonction de l’argument au carré :

Exemple 2

Dans ce deuxième exemple, nous dériverons l’arccotangente d’une fonction polynomiale du troisième degré.

Nous utilisons la règle de la dérivée arccotangente pour faire sa dérivation :

Donc la dérivée de l’arccotangente de la fonction est :