Hier erfahren Sie, was Konkavität und Konvexität einer Funktion sind und wie Sie erkennen können, ob eine Funktion konkav oder konvex ist. Darüber hinaus können Sie mit Schritt-für-Schritt-Übungen die Krümmung einer Funktion üben.
Was ist die Konkavität und Konvexität einer Funktion?
Konkavität und Konvexität einer Funktion beziehen sich auf die Krümmung des Graphen einer Funktion. Eine konkave Funktion ist eine Funktion, deren Graph die Form eines Berges hat, und eine konvexe Funktion ist eine Funktion, deren Graph die Form eines Tals hat.
Im vorherigen Absatz wurden konkave und konvexe Funktionen zum leichteren Verständnis informell definiert, die mathematische Definition der konkaven Funktion und der konvexen Funktion lautet jedoch wie folgt:
- Konkave Funktion: wenn das Segment, das zwei beliebige Punkte der Funktion verbindet, unterhalb der Kurve liegt.
- Konvexe Funktion: wenn das Segment, das zwei beliebige Punkte der Funktion verbindet, über der Kurve liegt.
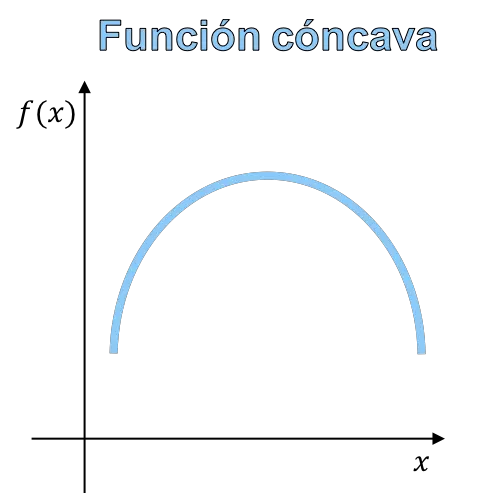

Letztendlich liegt der Unterschied zwischen einer konkaven Funktion und einer konvexen Funktion in der Form der Funktion. Daher können Sie Konkavität und Konvexität anhand des Funktionsgraphen unterscheiden.
Allerdings muss eine Funktion nicht unbedingt über ihren gesamten Definitionsbereich konkav oder konvex sein, sondern kann auch über ein Intervall konkav und über ein anderes Intervall konvex sein.
Hinweis: Die mathematische Gemeinschaft ist sich immer noch nicht ganz einig und daher sagen einige Professoren das Gegenteil: Sie nennen eine Funktion konkav, wenn sie die Form eines a hat
![]()
und eine konvexe Funktion, die die Form hat
![]()
. In jedem Fall ist es wichtig zu wissen, um welche Funktion es sich handelt, unabhängig vom Namen.
Wie man die Krümmung einer Funktion untersucht
Um die Krümmung einer Funktion zu untersuchen, müssen die Konkavität und Konvexität der Funktion ermittelt werden, d. h. die Intervalle, in denen die Funktion konkav ist, und die Intervalle, in denen die Funktion konvex ist.
Um die Krümmung einer Funktion zu untersuchen, müssen die folgenden Schritte ausgeführt werden:
- Finden Sie die Punkte, die nicht zum Definitionsbereich der Funktion gehören .
- Berechnen Sie die erste und zweite Ableitung der Funktion.
- Finden Sie die Wurzeln der zweiten Ableitung , das heißt, berechnen Sie durch Lösen die Punkte, die die zweite Ableitung aufheben
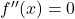
.
- Bilden Sie Intervalle mit den Wurzeln der Ableitung und den Punkten, die nicht zum Definitionsbereich der Funktion gehören.
- Berechnen Sie den Wert der zweiten Ableitung an einem Punkt in jedem Intervall.
- Somit bestimmt das Vorzeichen der zweiten Ableitung die Konkavität oder Konvexität der Funktion in diesem Intervall:
- Wenn die zweite Ableitung der Funktion positiv ist, ist die Funktion in diesem Intervall konvex .
- Wenn die zweite Ableitung der Funktion negativ ist, ist die Funktion in diesem Intervall konkav .
Beispiel für die Ermittlung der Krümmung einer Funktion
Als nächstes lösen wir Schritt für Schritt ein Beispiel, damit Sie sehen können, wie die Konkavitäts- und Konvexitätsintervalle einer Funktion berechnet werden.
- Untersuchen Sie die Konkavität und Konvexität der folgenden Funktion:
![]()
Als erstes muss der Definitionsbereich der Funktion berechnet werden. In diesem Fall haben wir eine Polynomfunktion, der Definitionsbereich der Funktion besteht also aus reellen Zahlen:
![]()
Nachdem wir den Definitionsbereich der Funktion berechnet haben, müssen wir untersuchen, an welchen Punkten die zweite Ableitung der Funktion verschwindet.
Wir berechnen daher die erste Ableitung der Funktion:
![]()
Wir finden dann die zweite Ableitung der Funktion:
![]()
Und nun setzen wir die zweite Ableitung gleich 0 und lösen die Gleichung:
![]()
![]()
![]()
![]()
Sobald wir den Definitionsbereich der Funktion und berechnet haben
![]()
, wir stellen alle kritischen Punkte dar, die auf der Linie gefunden werden. In diesem Fall haben wir keinen kritischen Punkt bei der Berechnung des Definitionsbereichs der Funktion gefunden, aber wir haben einen Punkt erhalten, der die zweite Ableitung der Funktion aufhebt:
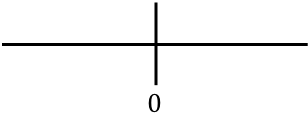
Und jetzt bewerten wir das Vorzeichen der zweiten Ableitung in jedem Intervall, um zu wissen, ob die Funktion konkav oder konvex ist. Wir nehmen daher in jedem Intervall einen Punkt (niemals die kritischen Punkte) und schauen uns an, welches Vorzeichen die zweite Ableitung an diesem Punkt hat:
![]()
![]()
![]()

Abschließend leiten wir die Konkavitäts- und Konvexitätsintervalle der Funktion ab. Wenn die zweite Ableitung positiv ist, bedeutet dies, dass die Funktion konvex ist.
![]()
, und wenn die zweite Ableitung negativ ist, bedeutet dies, dass die Funktion konkav ist
![]()
. Somit sind die Konkavitäts- und Konvexitätsintervalle der Funktion:
Konvex
![]()
:
![]()
Konkav
![]()
:
![]()
Gelöste Übungen zur Konkavität und Konvexität einer Funktion
Übung 1
Berechnen Sie die Konkavitäts- und Konvexitätsintervalle der folgenden Polynomfunktion:
![]()
Die Funktion in der Übung ist ein Polynom, der Definitionsbereich der Funktion besteht also aus reellen Zahlen:
![]()
Nachdem wir den Definitionsbereich der Funktion bestimmt haben, differenzieren wir sie:
![]()
Wir finden dann die zweite Ableitung der Funktion:
![]()
Und nun setzen wir die zweite Ableitung gleich 0 und lösen die Gleichung:
![]()
![]()
![]()
![]()
![]()
Sobald wir den Definitionsbereich der Funktion berechnet und gelöst haben
![]()
, wir stellen alle singulären Punkte dar, die auf der Zahlengeraden gefunden werden:

Und nun nehmen wir einen Punkt, der zu jedem Intervall gehört, und sehen, welches Vorzeichen die zweite Ableitung an diesem Punkt hat:
![]()
![]()

Wenn die zweite Ableitung größer als Null ist, bedeutet dies, dass die Funktion konvex ist.
![]()
, aber wenn die zweite Ableitung negativ ist, bedeutet dies, dass die Funktion konkav ist
![]()
. Daher sind die Konkavitäts- und Konvexitätsintervalle:
Konvex
![]()
:
![]()
Konkav
![]()
:
![]()
Übung 2
Untersuchen Sie die Krümmung der folgenden rationalen Funktion:
![]()
Zuerst müssen wir den Definitionsbereich der Funktion berechnen. Da es sich um eine rationale Funktion handelt, setzen wir den Nenner gleich Null, um zu sehen, welche Zahlen nicht zum Definitionsbereich der Funktion gehören:
![]()
![]()
![]()
![]()
Das heißt, wenn x -2 oder +2 ist, ist der Nenner 0. Daher existiert die Funktion nicht. Der Definitionsbereich der Funktion besteht daher aus allen Zahlen außer x=-2 und x=+2.
![]()
Zweitens berechnen wir die erste Ableitung der Funktion:
![]()
![]()
Und dann lösen wir die zweite Ableitung:


Alle Terme werden mit multipliziert
![]()
. Wir können den Bruch daher vereinfachen:

![]()
![]()
![]()
![]()
Berechnen wir nun die Wurzeln der zweiten Ableitung der Funktion:
![]()
![]()
Der Begriff
![]()
Dazu müssen wir die gesamte linke Seite dividieren, damit wir sie mit der gesamten rechten Seite multiplizieren können:
![]()
![]()
Wir extrahieren den gemeinsamen Faktor:
![]()
Damit die Multiplikation gleich 0 ist, muss eines der beiden Elemente der Multiplikation Null sein. Deshalb setzen wir jeden Faktor gleich 0:
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
Es gibt keine Lösung, da es keine negative Wurzel einer reellen Zahl gibt.
Wir stellen nun auf der Geraden alle erhaltenen kritischen Punkte dar, also die Punkte, die nicht zum Definitionsbereich gehören (x=-2 und x=+2) und diejenigen, die die zweite Ableitung aufheben (x=0):

Und wir bewerten das Vorzeichen der zweiten Ableitung in jedem Intervall, um zu wissen, ob die Funktion konkav oder konvex ist. Wir nehmen also einen Punkt in jedem Intervall und schauen uns an, welches Vorzeichen die zweite Ableitung an diesem Punkt hat:
![]()
![]()
![]()
![]()

Wenn die zweite Ableitung positiv ist, bedeutet dies, dass die Funktion konvex ist.
![]()
, und wenn die zweite Ableitung negativ ist, bedeutet dies, dass die Funktion konkav ist
![]()
. Die Konkavitäts- und Konvexitätsintervalle sind daher:
Konvex
![]()
:
![]()
Konkav
![]()
:
![]()
Übung 3
Eine Funktion
![]()
hat ein relatives Extrem in
![]()
. Und außerdem ist die Funktion konvex
![]()
an diesem Punkt. Bestimmen Sie, ob das relative Extrem ein Minimum oder ein Maximum ist.
➤ Siehe: Definition von Maxima und Minima einer Funktion
Sei die konvexe Funktion
![]()
In
![]()
bedeutet, dass die zweite Ableitung an dieser Stelle positiv ist, d. h
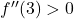 Daher ist das relative Extrem von
Daher ist das relative Extrem von
![]()
Dies ist ein Minimum , da
![]()
Es ist positiv.