Darstellung von Funktionen -

In diesem Artikel erfahren Sie , wie Sie jede Art von Funktion in einem Diagramm darstellen. Darüber hinaus finden Sie gelöste Schritt-für-Schritt-Übungen zur Darstellung von Funktionen in einem Diagramm.

So stellen Sie eine Funktion in einem Diagramm dar

Um eine Funktion in einem Diagramm darzustellen, müssen die folgenden Schritte ausgeführt werden:

Finden Sie den Definitionsbereich der Funktion.
Berechnen Sie die Grenzwerte der Funktion mit den kartesischen Achsen.
Berechnen Sie die Asymptoten der Funktion.
Untersuchen Sie die Monotonie der Funktion und finden Sie ihre relativen Extreme .
Studieren Sie die Krümmung der Funktion und finden Sie ihre Wendepunkte .
Zeichnen Sie die Grenzwerte, Asymptoten, relativen Extrema und Wendepunkte ein und zeichnen Sie dann die Funktion.

Beispiel für die Darstellung einer Funktion

Damit Sie sehen können, wie eine Funktion grafisch dargestellt wird, lösen wir folgende Übung Schritt für Schritt:

Zeichnen Sie die folgende rationale Funktion in ein Diagramm:

$f(x)=\cfrac{x^2}{x-1}$

Als erstes muss der Definitionsbereich der Funktion berechnet werden . Da es sich um eine rationale Funktion handelt, müssen wir den Nenner auf Null setzen, um zu sehen, welche Zahlen nicht zum Definitionsbereich der Funktion gehören:

$x-1=0$

$x=1$

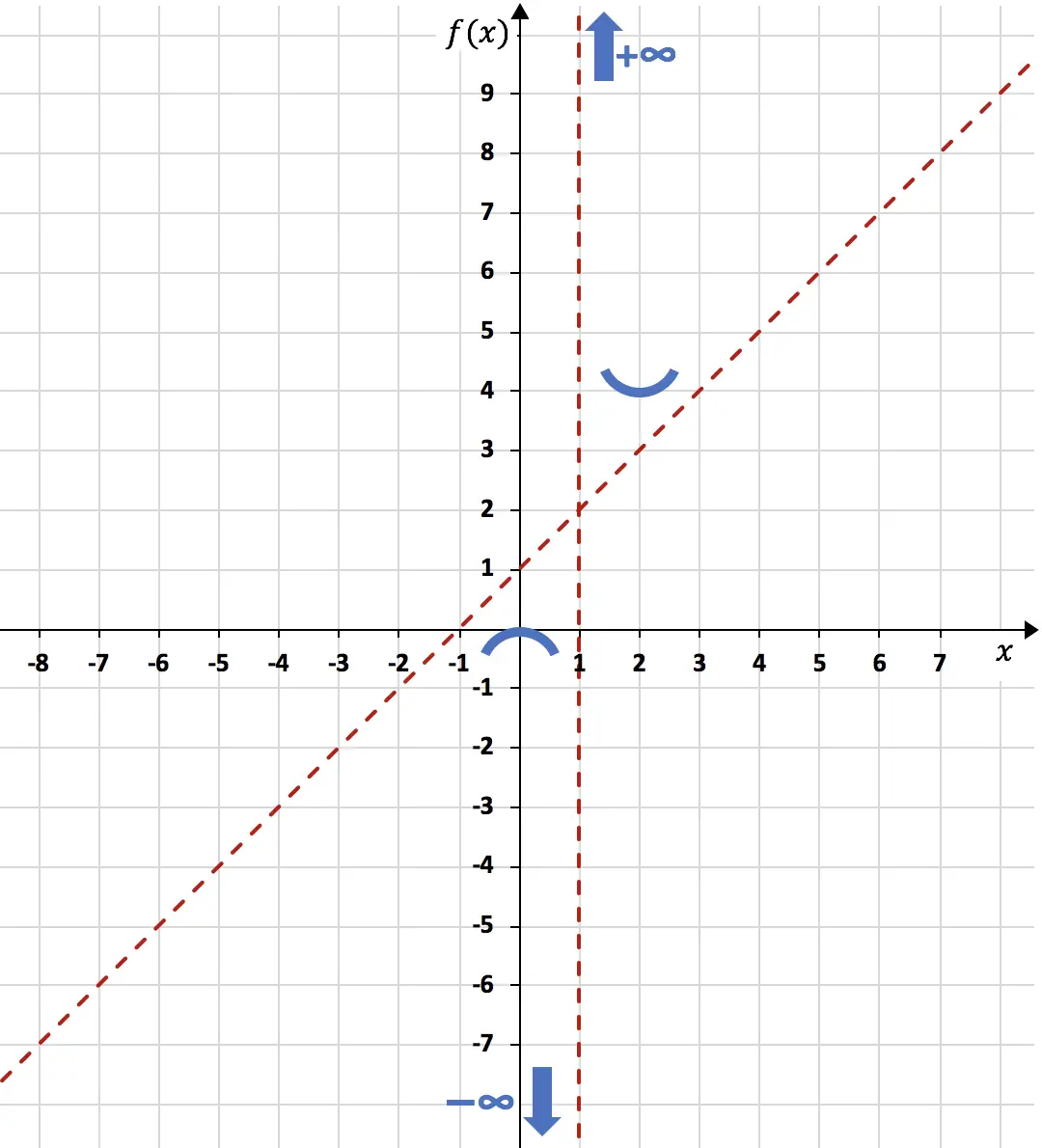
Wenn x also 1 ist, ist der Nenner 0 und die Funktion existiert daher nicht. Der Definitionsbereich der Funktion besteht daher aus allen reellen Zahlen außer x=1.

$\text{Dom } f= \mathbb{R}-\{1 \}$

Um den Schnittpunkt mit der X-Achse zu finden, müssen wir die Gleichung lösen

$f(x)= 0.$

Da die Funktion auf der X-Achse immer den Wert 0 hat:

$f(x)=0$

$\cfrac{x^2}{x-1} = 0$

Der Begriff

$x -1$

Dazu müssen wir die gesamte linke Seite dividieren, damit wir sie mit der gesamten rechten Seite multiplizieren können:

$x^2 = 0 \cdot (x-1)$

$x^2 = 0$

$x = 0$

Der Schnittpunkt mit der OX-Achse ist also:

$\bm{(0,0)}$

Und um den Schnittpunkt mit der Y-Achse zu finden, rechnen wir

$f(0).$

Weil x auf der Y-Achse immer 0 ist:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0$

Daher ist der Grenzwert mit der OY-Achse:

$\bm{(0,0)}$

Wenn die Funktion in diesem Fall durch den Koordinatenursprung verläuft, fällt der Schnittpunkt mit der X-Achse mit dem Schnittpunkt mit der Y-Achse zusammen.

Sobald wir den Definitionsbereich und die Grenzwerte kennen, müssen wir die Asymptoten der Funktion berechnen .

Um zu sehen, ob die Funktion vertikale Asymptoten hat, müssen wir den Grenzwert der Funktion an Punkten berechnen, die nicht zum Definitionsbereich gehören (in diesem Fall x=1). Und wenn das Ergebnis unendlich ist, ist es eine vertikale Asymptote. Noch:

$\displaystyle \lim_{x \to 1} \ \cfrac{x^2}{x-1} = \cfrac{1^2}{1-1} = \cfrac{1}{0} = \infty$

Da der Grenzwert der Funktion, wenn x gegen 1 tendiert, Unendlich ergibt, ist x=1 eine vertikale Asymptote:

stellen Funktionen dar, vertikale Asymptote

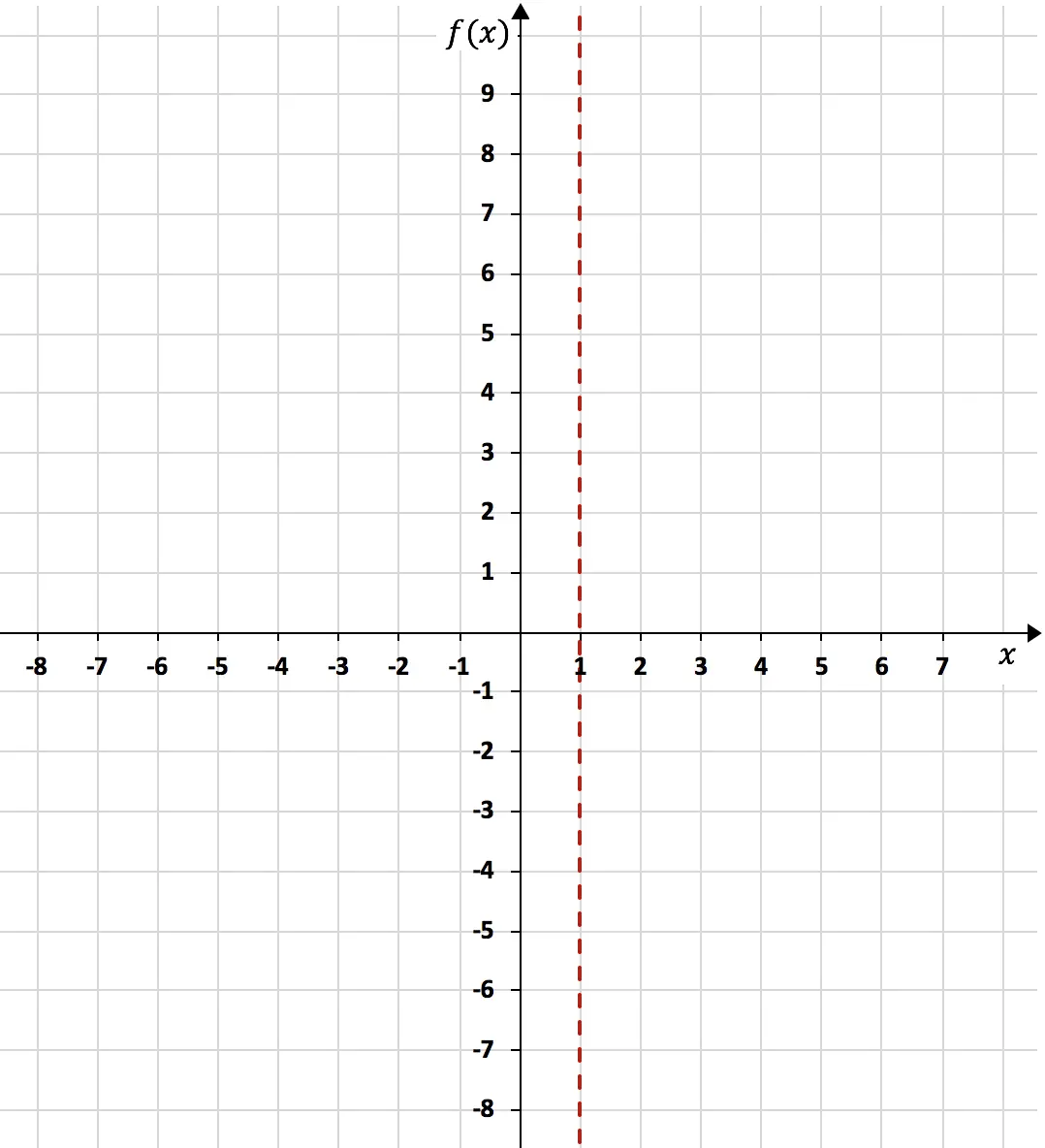
Nachdem die vertikale Asymptote berechnet wurde, müssen die seitlichen Grenzen der Funktion in Bezug auf sie berechnet werden. Da wir nicht wissen, ob die Funktion zu -∞ oder +∞ tendiert, wenn sie sich von links x=1 nähert, und wir nicht wissen, wann sie sich von rechts x=1 nähert.

Daher berechnen wir den linken seitlichen Grenzwert der Funktion bei x=1:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1}$

Um eine seitliche Grenze an einem Punkt numerisch zu berechnen, müssen wir eine Zahl in die Funktion einsetzen, die sehr nahe am Punkt liegt. In diesem Fall möchten wir links eine Zahl sehr nahe bei 1 haben, beispielsweise 0,9. Wir ersetzen daher den Punkt 0,9 in der Funktion:

$\cfrac{0,9^2}{0,9-1}=\cfrac{0,81}{-0,1}=-81$

Seitliche Grenzen einer Asymptote können nur +∞ oder -∞ ergeben. Und da wir durch Einsetzen einer Zahl sehr nahe bei 1 auf der linken Seite in die Funktion ein negatives Ergebnis erhalten haben, ist die Grenze auf der linken Seite -∞:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1} = \bm{-\infty}$

Jetzt machen wir das gleiche Verfahren mit der rechten Seitengrenze:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1}$

Wir setzen rechts in die Funktion eine Zahl ein, die sehr nahe bei 1 liegt. Zum Beispiel Punkt 1.1:

$\cfrac{1,1^2}{1,1-1}=\cfrac{1,21}{0,1}=+12,1$

In diesem Fall ist das Ergebnis der Nebengrenze eine positive Zahl. Der Grenzwert rechts ist also +∞:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1} = \bm{+\infty}$

Zusammenfassend lässt sich sagen, dass die Funktion bei x=1 links in Richtung minus Unendlich und rechts in Richtung plus Unendlich tendiert:

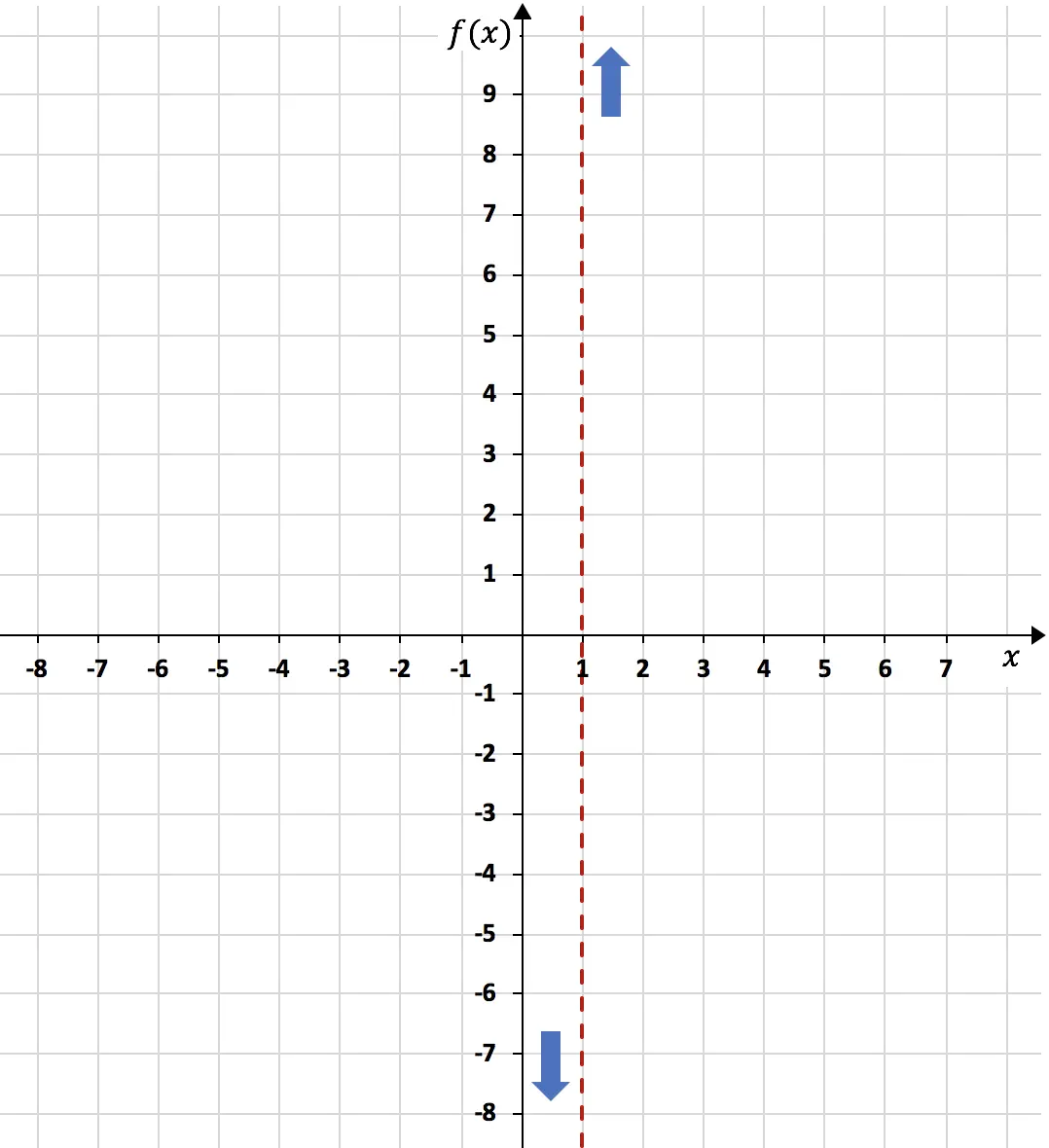
grafische Funktionen, vertikale Asymptote

Andererseits ist die horizontale Asymptote der Funktion das Ergebnis der unendlichen Grenze der Funktion. Noch:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2}{x-1} = \cfrac{+\infty}{+\infty } =+\infty$

Denken Sie daran, wie man die unendlichen Grenzen rationaler Funktionen berechnet:

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.“ title=“Rendered by QuickLaTeX.com“ height=“139″ width=“767″ style=“vertical-align: 0px;“> </div> Der unendliche Grenzwert der Funktion gab uns +∞, daher hat die Funktion keine horizontale Asymptote. Wir berechnen nun die schräge Asymptote. Die schrägen Asymptoten haben die Form <p class=$ $y=mx+n$

. UND

$m$

Die Berechnung erfolgt nach folgender Formel:

$\displaystyle m = \lim_{x \to +\infty} f(x):x$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:x$

Das x ist so, als hätte es eine 1 als Nenner:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:\cfrac{x}{1}$

Es handelt sich um eine Division von Brüchen, also multiplizieren wir sie quer:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 \cdot 1 }{(x-1) \cdot x}$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x}$

Und wir berechnen den Grenzwert:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x} = \cfrac{+\infty}{+\infty } = \cfrac{1}{1} = 1$

Also m=1. Jetzt rechnen wir

$n$

mit folgender Formel:

$\displaystyle n = \lim_{x \to +\infty} \bigl[f(x)-mx\bigr]$

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty$

Aber wir erhalten die Unbestimmtheit Unendlich minus Unendlich, also müssen wir die Terme auf einen gemeinsamen Nenner bringen. Dazu multiplizieren und dividieren wir den Term x durch den Nenner des Bruchs:

$\displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]$

Da die beiden Begriffe nun denselben Nenner haben, können wir sie gruppieren:

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]$

Und schließlich lösen wir das Limit:

$\displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1$

Also n = 1. Die schräge Asymptote ist daher:

$y = mx+n$

$y = 1x+1$

$\bm{y = x+1}$

Nachdem wir die schräge Asymptote berechnet haben, stellen wir sie im selben Diagramm dar, indem wir eine Wertetabelle erstellen:

$y=x+1$

$\begin{array}{c|c} x & y \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array}$

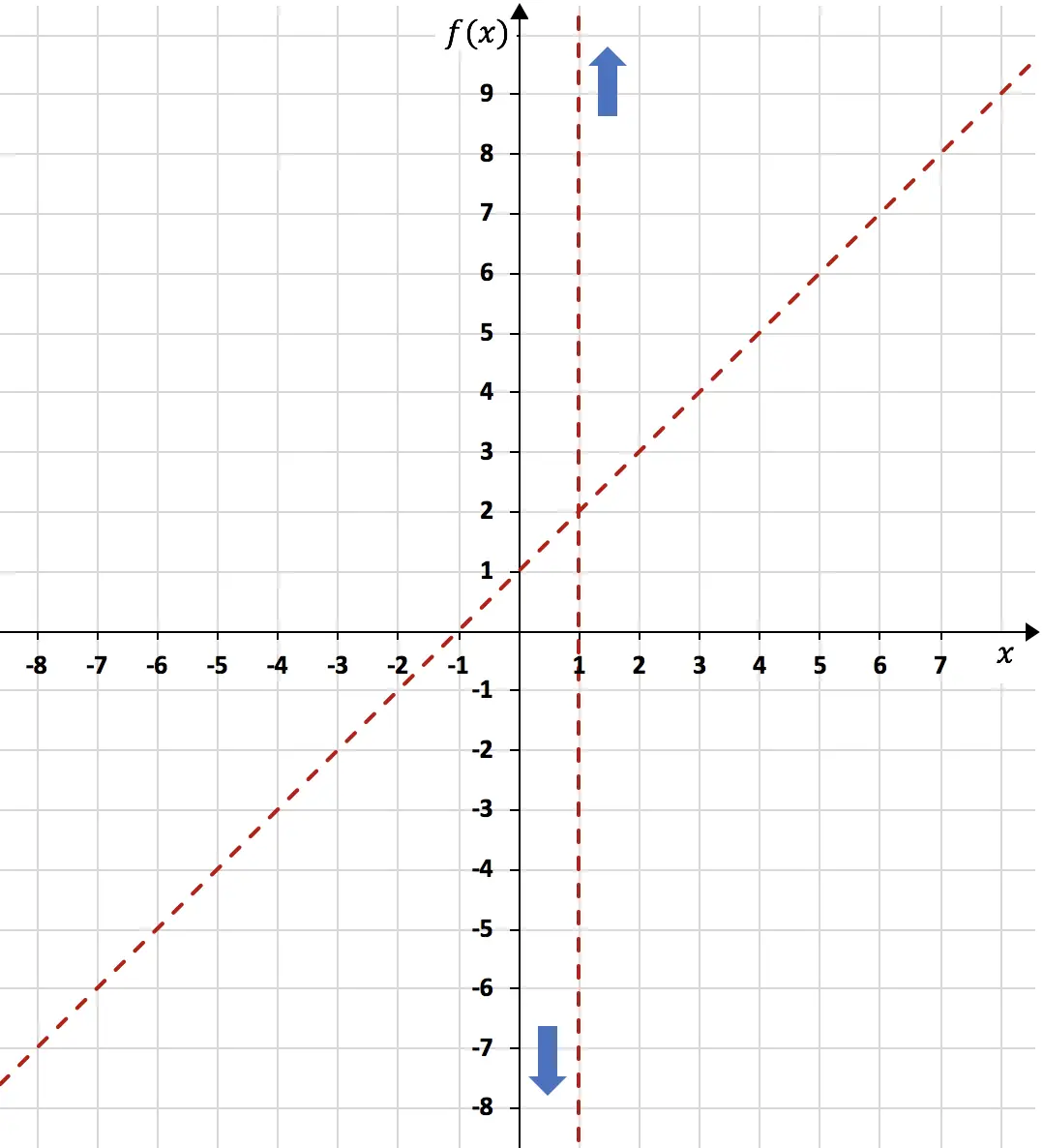
stellen Funktionen dar, schräge Asymptote

Da wir nun alle Asymptoten der Funktion kennen, müssen wir die Monotonie der Funktion analysieren. Das heißt, wir müssen untersuchen, in welchen Intervallen die Funktion zunimmt und in welchen Intervallen sie abnimmt. Wir berechnen daher die erste Ableitung der Funktion:

$f(x)=\cfrac{x^2}{x-1} \ \longrightarrow \ f'(x)= \cfrac{2x\cdot (x-1) - x^2 \cdot 1}{(x-1)^2}$

$f'(x)= \cfrac{2x^2-2x - x^2}{(x-1)^2} = \cfrac{x^2-2x}{(x-1)^2}$

Und nun setzen wir die Ableitung gleich 0 und lösen die Gleichung:

$f'(x)=0$

$\cfrac{x^2-2x}{(x-1)^2}=0$

Der Begriff

$\left(x-1\right)^2}$

Dazu müssen wir die gesamte linke Seite dividieren, damit wir sie mit der gesamten rechten Seite multiplizieren können:

$x^2-2x=0\cdot \left(x-1\right)^2$

$x^2-2x=0$

Wir extrahieren den gemeinsamen Faktor, um die quadratische Gleichung zu lösen:

$x(x-2)=0$

Damit die Multiplikation gleich 0 ist, muss eines der beiden Elemente der Multiplikation Null sein. Daher setzen wir jeden Faktor gleich 0 und erhalten beide Lösungen der Gleichung:

$\displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}$

Auf dem Zahlenstrahl stellen wir nun alle gefundenen kritischen Punkte dar, also die Punkte, die nicht zum Definitionsbereich gehören (x=1) und diejenigen, die die Ableitung aufheben (x=0 und x=2):

Und wir bewerten das Vorzeichen der Ableitung in jedem Intervall, um zu wissen, ob die Funktion zunimmt oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals die kritischen Punkte) und schauen uns an, welches Vorzeichen die Ableitung an diesem Punkt hat:

$f'(x)=\cfrac{x^2-2x}{\left(x-1\right)^2}$

$f'(-1) = \cfrac{(-1)^2-2(-1)}{\left((-1)-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

$f'(0,5) = \cfrac{0,5^2-2\cdot 0,5}{\left(0,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(1,5) = \cfrac{1,5^2-2\cdot 1,5}{\left(1,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(3) = \cfrac{3^2-2\cdot 3}{\left(3-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

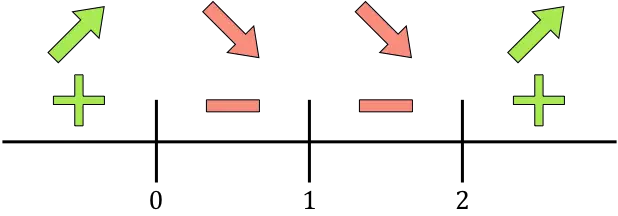
Wenn die Ableitung positiv ist, bedeutet dies, dass die Funktion zunimmt, und wenn die Ableitung negativ ist, bedeutet dies, dass die Funktion abnimmt. Daher sind die Wachstums- und Rückgangsintervalle:

Wachstum:

$\bm{(-\infty, 0)\cup (2,+\infty)}$

Verringern:

$\bm{(0,1)\cup (1,2)}$

Darüber hinaus geht die Funktion bei x=0 von steigender zu fallender Funktion über, sodass x=0 ein relatives Maximum der Funktion ist. Und bei x=2 geht die Funktion von fallend zu steigend über, sodass x=2 ein relatives Minimum der Funktion ist.

Schließlich ersetzen wir die gefundenen Extrema in der ursprünglichen Funktion, um die Y-Koordinate der Punkte zu ermitteln:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0 \ \longrightarrow \ (0,0)$

$f(2)=\cfrac{2^2}{2-1} = \cfrac{4}{1} = 4 \ \longrightarrow \ (2,4)$

Die relativen Extremwerte der Funktion sind daher:

Maximal auf den Punkt gebracht

$\bm{(0,0)}$

Minimum bis Punkt

$\bm{(2,4)}$

Wir stellen das Maximum und das Minimum in der Grafik dar:

stellen die Maximal- und Minimalfunktionen dar

Schließlich genügt es, die Krümmung der Funktion zu untersuchen , also die Konkavitäts- und Konvexitätsintervalle der Funktion zu untersuchen. Dazu berechnen wir seine zweite Ableitung:

$f'(x)=\cfrac{x^2-2x}{(x-1)^2} \ \longrightarrow \ f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)\cdot 1}{\left(\left(x-1\right)^2\right)^2}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)}{(x-1)^4}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^{\cancel{2}}- (x^2-2x)\cdot 2\cancel{(x-1)}}{(x-1)^{\cancelto{3}{4}}} = \cfrac{(2x-2)\cdot (x-1)- (x^2-2x)\cdot 2}{(x-1)^3}$

$f''(x)= \cfrac{2x^2-2x-2x+2- (2x^2-4x)}{(x-1)^3} =\cfrac{2x^2-2x-2x+2- 2x^2+4x}{(x-1)^3}$

$f''(x) =\cfrac{2}{(x-1)^3}$

Und nun setzen wir die zweite Ableitung gleich Null und lösen die Gleichung:

$f''(x)=0$

$\cfrac{2}{(x-1)^3} =0$

$2=0\cdot \left(x-1\right)^3$

$2=0$

2 wird niemals gleich 0 sein, also die Gleichung

$f''(x)=0$

Es gibt keine Lösung.

Wir stellen nun auf dem Zahlenstrahl alle gefundenen kritischen Punkte dar, also die Punkte, die nicht zum Definitionsbereich (x=1) gehören, und diejenigen, die die zweite Ableitung aufheben (in diesem Fall gibt es keine hat nicht):

Und wir bewerten das Vorzeichen der Ableitung in jedem Intervall, um zu wissen, ob die Funktion konvex oder konkav ist. Wir nehmen daher in jedem Intervall einen Punkt (niemals die singulären Punkte) und schauen uns an, welches Vorzeichen die Ableitung an dieser Stelle hat:

$f''(x) =\cfrac{2}{(x-1)^3}$

$f''(0) =\cfrac{2}{(0-1)^3} = \cfrac{2}{-1}=-2 \ \rightarrow \ \bm{-}$

$f''(2) =\cfrac{2}{(2-1)^3} = \cfrac{2}{1}=2 \ \rightarrow \ \bm{+}$

Und schließlich leiten wir die Konkavitäts- und Konvexitätsintervalle der Funktion ab. Wenn die zweite Ableitung positiv ist, bedeutet dies, dass die Funktion konvex ist.

$(\bm{\cup})$

, und wenn die zweite Ableitung negativ ist, bedeutet dies, dass die Funktion konkav ist

$(\bm{\cap})$

. Die Konkavitäts- und Konvexitätsintervalle sind daher:

Konvex

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Konkav

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Obwohl es bei x=1 zu einer Krümmungsänderung kommt, handelt es sich jedoch nicht um einen Wendepunkt. Weil x=1 nicht zum Definitionsbereich der Funktion gehört.

So können wir die Darstellung der Funktion mit allem, was wir berechnet haben, abschließen:

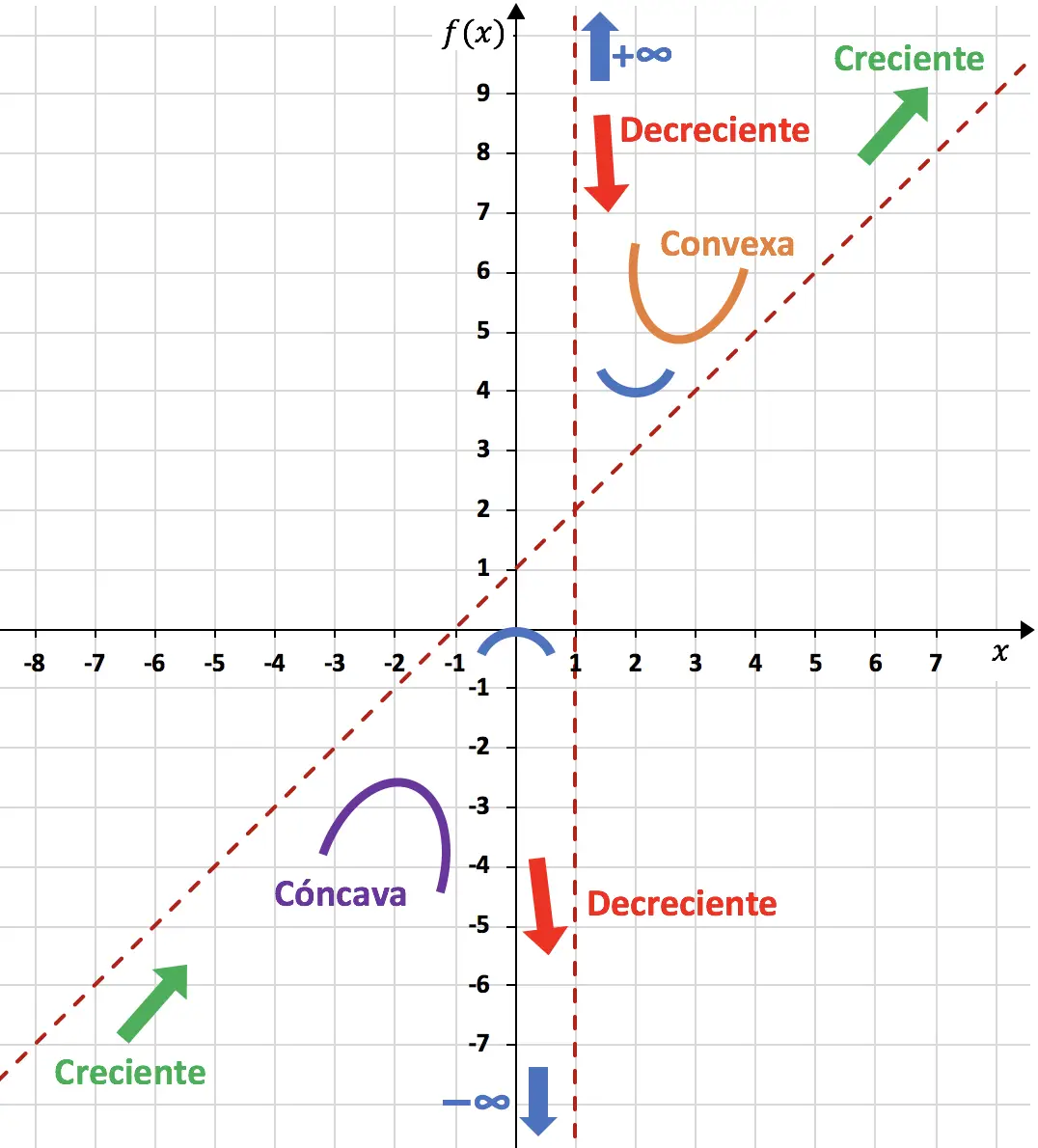
Die im Diagramm dargestellte Funktion sieht daher folgendermaßen aus:

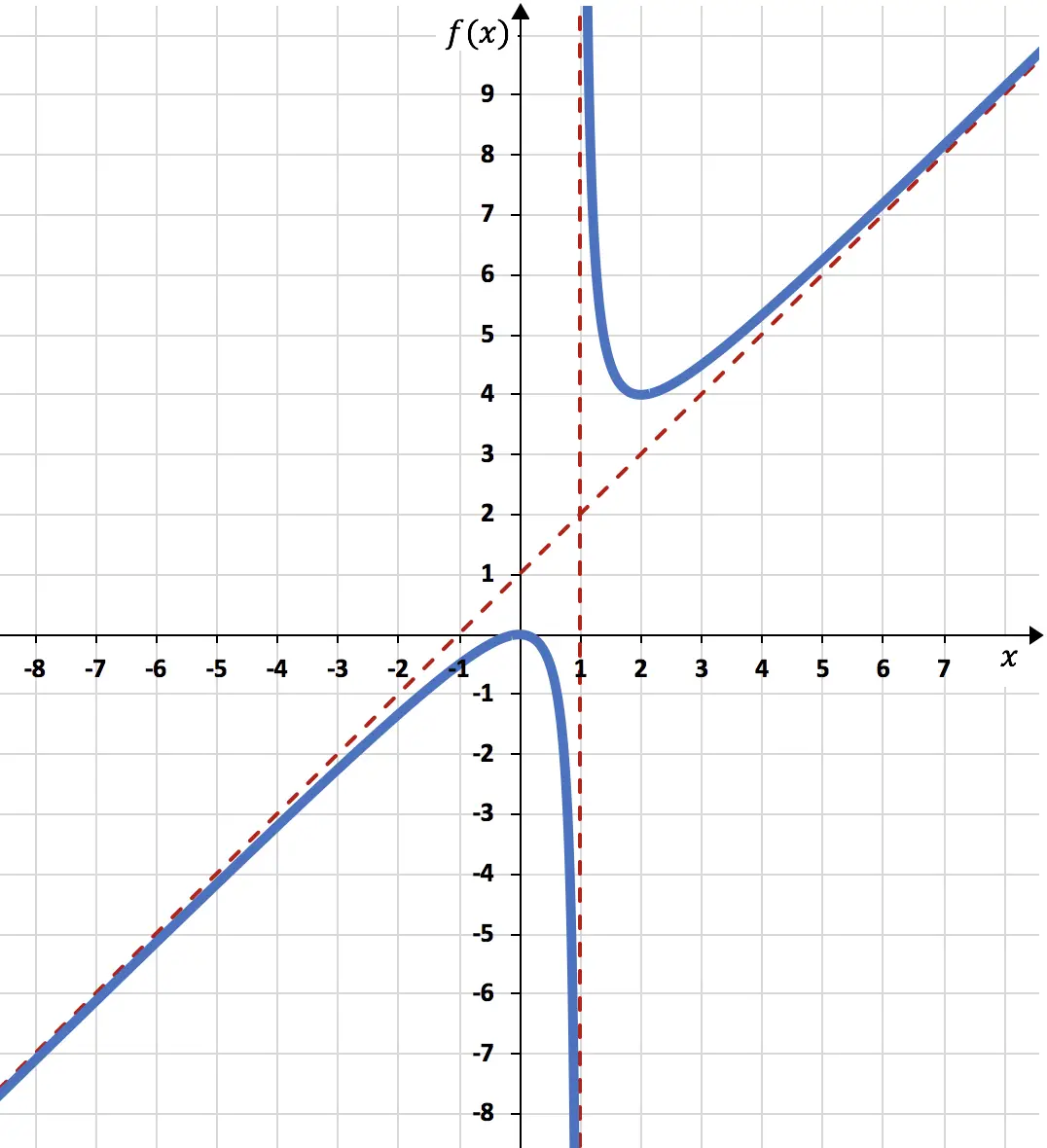
grafische Darstellung der rationalen Funktion

Aufgaben zur Darstellung von Funktionen gelöst

Übung 1

Stellen Sie die folgende Polynomfunktion grafisch dar:

$\displaystyle f(x)=x^3-3x^2+4$

Sehen Sie sich die Lösung an

Als erstes muss der Definitionsbereich der Funktion berechnet werden. Da es sich um eine Polynomfunktion handelt, besteht der Definitionsbereich nur aus reellen Zahlen:

$\text{Dom } f= \mathbb{R}$

Um den Schnittpunkt mit der X-Achse zu finden, lösen wir

$f(x)= 0.$

$f(x)=0$

$x^3-3x^2+4=0$

Dies ist eine Gleichung mit einem Grad größer als 2. Daher faktorisieren wir die Gleichung:

$(x+1)(x^2-4x+4)=0$

Also ist x=-1 eine Lösung. Und wir berechnen die anderen Lösungen, indem wir die resultierende quadratische Gleichung lösen:

$\begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}$

Die Schnittpunkte mit der X-Achse sind also:

$\bm{(-1,0)}$

Und

$\bm{(2,0)}$

Und um den Schnittpunkt mit der Y-Achse zu finden, berechnen wir

$f(0).$

Da x auf der Y-Achse immer 0 ist:

$f(0)=0^3-3\cdot0^2+4 = 4$

Der Schnittpunkt mit der Y-Achse ist also:

$\bm{(0,4)}$

Um zu sehen, ob die Funktion vertikale Asymptoten hat, müssen wir den Grenzwert der Funktion an Punkten berechnen, die nicht zum Definitionsbereich gehören. In diesem Fall umfasst der Definitionsbereich alle reellen Zahlen. Die Funktion hat daher keine vertikale Asymptote.

Andererseits ist die horizontale Asymptote der Funktion das Ergebnis der unendlichen Grenze der Funktion. Noch:

$\displaystyle \lim_{x \to +\infty} \ x^3-3x^2+4 =(+\infty)^3 = +\infty$

Der unendliche Grenzwert der Funktion gab uns +∞, daher hat die Funktion keine horizontale Asymptote.

Wir berechnen nun die schräge Asymptote. Die schrägen Asymptoten haben die Form

$y=mx+n.$

UND

$m$

Die Berechnung erfolgt nach folgender Formel:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \left( x^3-3x^2+4\right): x =$

$\displaystyle = \lim_{x \to +\infty} \cfrac{x^3-3x^2+4}{x} = \cfrac{+\infty}{+\infty} = +\infty$

Der Grenzwert gab uns +∞, daher hat die Funktion auch keine schiefe Asymptote.

Um die Monotonie der Funktion zu untersuchen, müssen wir zunächst ihre Ableitung berechnen:

$f(x)= x^3-3x^2+4 \ \longrightarrow \ f'(x)= 3x^2-6x$

Nun setzen wir die Ableitung gleich 0 und lösen die Gleichung:

$f'(x)= 0$

$3x^2-6x=0$

$x(3x-6)=0$

$\displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}$

Wir stellen nun auf der Zahlengeraden alle erhaltenen singulären Punkte dar, d. h. die Punkte, die nicht zum Definitionsbereich gehören (in diesem Fall gehören sie alle dazu) und diejenigen, die die Ableitung aufheben (x=0 und x =2). :

Und wir bewerten das Vorzeichen der Ableitung in jedem Intervall, um zu wissen, ob die Funktion zunimmt oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals die singulären Punkte) und schauen uns an, welches Vorzeichen die Ableitung an dieser Stelle hat:

$f'(-1)=3(-1)^2-6(-1)= 3+6 = 9\ \rightarrow \ \bm{+}$

$f'(1)=3\cdot 1^2-6\cdot 1= 3-6 = -3\ \rightarrow \ \bm{-}$

$f'(3)=3\cdot 3^2-6\cdot 3= 27-18 = 9\ \rightarrow \ \bm{+}$

Wachstum:

$\bm{(-\infty,0)\cup (2,+\infty)}$

Verringern:

$\bm{(0,2)}$

Die Funktion geht bei x=0 vom Ansteigenden zum Absteigenden über, sodass x=0 ein Maximum der Funktion ist. Und die Funktion geht bei x=2 von abnehmend zu steigend über, sodass x=2 ein Minimum der Funktion ist.

Schließlich ersetzen wir die gefundenen Extrema in der ursprünglichen Funktion, um die Y-Koordinaten der Punkte zu ermitteln:

$f(0)=0^3-3\cdot 0^2+4 = 4 \ \longrightarrow \ (0,4)$

$f(2)=2^3-3\cdot 2^2+4 = 8-3 \cdot 4 +4 = 0 \ \longrightarrow \ (2,0)$

Die relativen Extremwerte der Funktion sind daher:

Maximal auf den Punkt gebracht

$\bm{(0,4)}$

Minimum bis Punkt

$\bm{(2,0)}$

Um die Krümmung der Funktion zu untersuchen, berechnen wir ihre zweite Ableitung:

$f'(x)= 3x^2-6x \ \longrightarrow \ f''(x)= 6x-6$

Nun setzen wir die zweite Ableitung gleich 0 und lösen die Gleichung:

$f''(x)= 0$

$6x-6=0$

$6x=6$

$x= \cfrac{6}{6} = 1$

Wir stellen auf der Geraden alle gefundenen singulären Punkte dar, also die Punkte, die nicht zum Definitionsbereich gehören (in diesem Fall gehören sie alle dazu) und diejenigen, die die Ableitung aufheben (x=1):

Und jetzt bewerten wir das Vorzeichen der zweiten Ableitung in jedem Intervall, um zu wissen, ob die Funktion konkav oder konvex ist. Wir nehmen daher in jedem Intervall einen Punkt (niemals die singulären Punkte) und schauen uns an, welches Vorzeichen die zweite Ableitung an dieser Stelle hat:

$f''(0)=6\cdot 0-6= -6 \ \rightarrow \ \bm{-}$

$f''(2)=6\cdot 2-6= 12-6= 6 \ \rightarrow \ \bm{+}$

Wenn die zweite Ableitung positiv ist, bedeutet dies, dass die Funktion konvex ist.

$(\bm{\cup})$

, und wenn die zweite Ableitung negativ ist, bedeutet dies, dass die Funktion konkav ist

$(\bm{\cap})$

. Die Konkavitäts- und Konvexitätsintervalle sind daher:

Konvex

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Konkav

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Darüber hinaus ändert sich die Funktion bei x=1 von konkav zu konvex, sodass x=1 ein Wendepunkt der Funktion ist.

Schließlich ersetzen wir die gefundenen Wendepunkte in der ursprünglichen Funktion, um die Y-Koordinate der Punkte zu ermitteln:

$f(1)=1^3-3\cdot 1^2+ 4= 1 -3 +4 =2 \ \longrightarrow \ (1,2)$

Die Wendepunkte der Funktion sind also:

Wendepunkte:

$\bm{(1,2)}$

Basierend auf allen von uns berechneten Informationen stellen wir abschließend die Funktion grafisch dar:

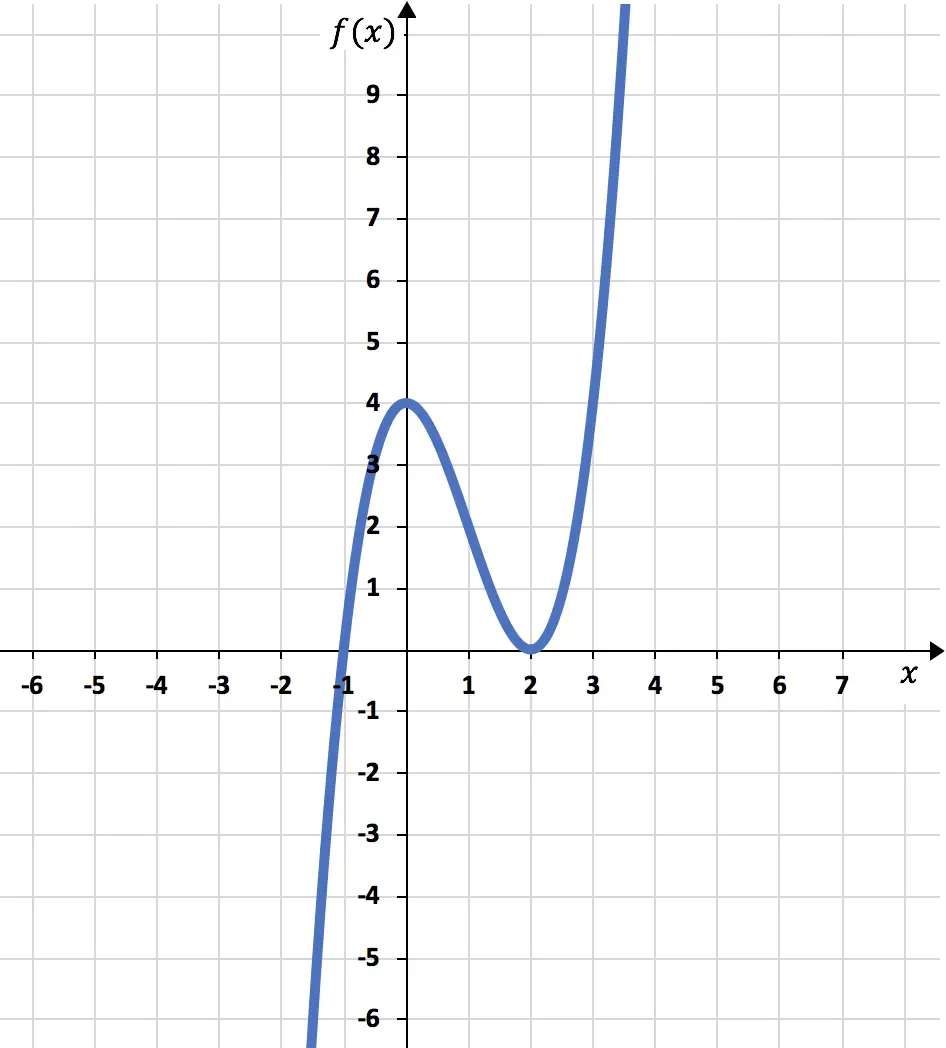
grafische Darstellung der Polynomfunktion

Übung 2

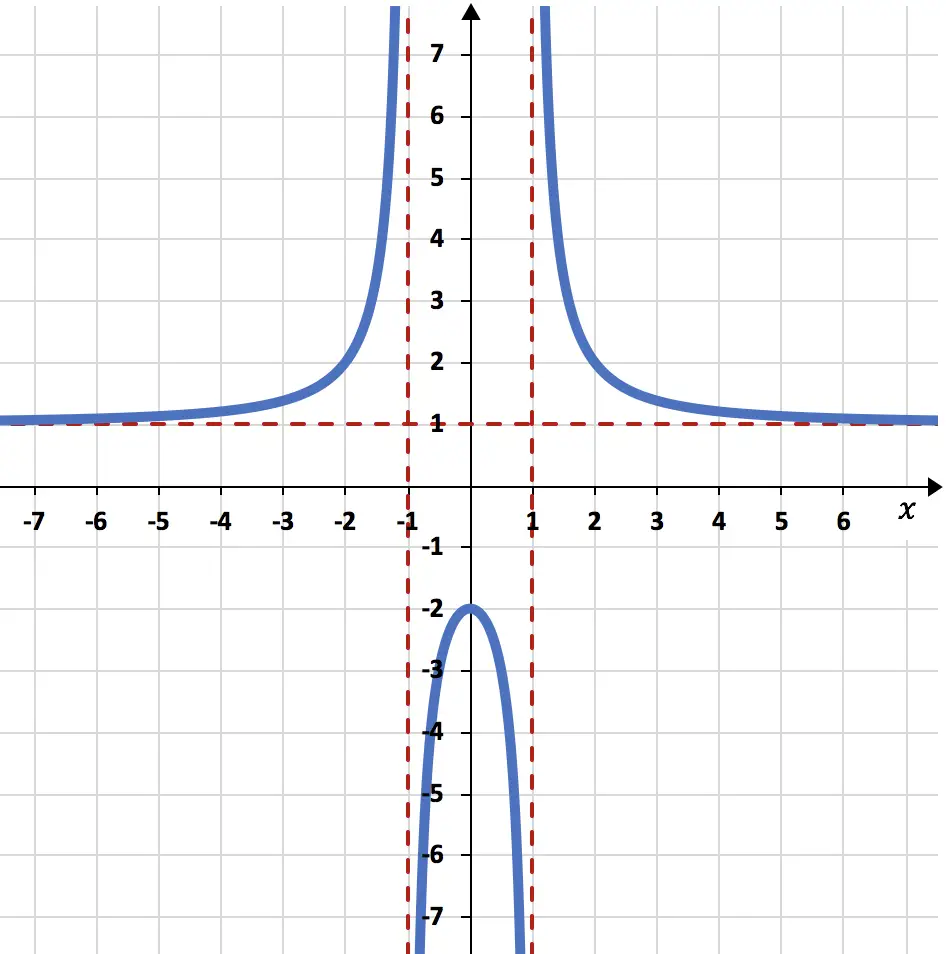
Stellen Sie die folgende rationale Funktion grafisch dar:

$\displaystyle f(x)=\frac{x^2+2}{x^2-1}$

Sehen Sie sich die Lösung an

Um den Definitionsbereich der Funktion zu finden, setzen wir den Nenner gleich. Bringe den Bruch auf Null und löse die resultierende Gleichung:

$x^2-1= 0$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm 1$

$\text{Dom } f= \mathbb{R}-\{-1, +1 \}$

Zweitens bestimmen wir die Schwellenwerte der Funktion, wobei die x-Achse dem algebraischen Ausdruck der Funktion entspricht. Stahl:

$f(x)=0$

$\cfrac{x^2+2}{x^2-1}=0$

$x^2+2=0\cdot (x^2-1)$

$x^2+2=0$

$x^2=-2$

$x=\sqrt{-2} \quad \color{red}\bm{\times}$

Es gibt keine Quadratwurzel einer negativen Zahl. Daher schneidet die Funktion die X-Achse nicht.

Und um den Schnittpunkt mit der Computerachse zu finden, werten wir die Funktion bei x=0 aus.

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2$

Der Schnittpunkt mit der Y-Achse ist also:

$\bm{(0,-2)}$

Um zu sehen, ob die Funktion vertikale Asymptoten hat, müssen wir den Grenzwert der Funktion an Punkten berechnen, die nicht zum Definitionsbereich gehören (in diesem Fall x=-1 und x=+1). Und wenn das Ergebnis unendlich ist, ist es eine vertikale Asymptote. Noch:

$\displaystyle \lim_{x \to -1} \cfrac{x^2+2}{x^2-1} = \cfrac{(-1)^2+2}{(-1)^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

Da der Grenzwert der Funktion bei Annäherung von x an -1 Unendlich ergibt, ist x=-1 eine vertikale Asymptote.

Wir berechnen die seitlichen Grenzen der Asymptote x=-1, indem wir eine Zahl sehr nahe bei ihr in die Funktion einsetzen:

$\displaystyle f(-1,1)=\cfrac{(-1,1)^2+2}{(-1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to -1^{-}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

$\displaystyle f(-0,9)=\cfrac{(-0,9)^2+2}{(-0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to -1^{+}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

Schauen wir uns nun an, ob x=+1 eine vertikale Asymptote ist:

$\displaystyle \lim_{x \to +1} \cfrac{x^2+2}{x^2-1} = \cfrac{1^2+2}{1^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

Da der Grenzwert der Funktion, wenn x sich +1 nähert, Unendlich ergibt, ist x=+1 eine vertikale Asymptote.

Wir berechnen die seitlichen Grenzen der Asymptote x=1, indem wir eine Zahl, die ihr sehr nahe kommt, in die Funktion einsetzen:

$\displaystyle f(0,9)=\cfrac{(0,9)^2+2}{(0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to +1^{-}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

$\displaystyle f(1,1)=\cfrac{(1,1)^2+2}{(1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to +1^{+}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

Andererseits ist die horizontale Asymptote der Funktion das Ergebnis der unendlichen Grenze der Funktion. Noch:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2+2}{x^2-1} = \cfrac{+\infty}{+\infty } =\cfrac{1}{1} = 1$

Der unendliche Grenzwert der Funktion ergab 1, daher hat die Funktion eine horizontale Asymptote bei y=1.

Da die Funktion eine horizontale Asymptote hat, wird sie keine schräge Asymptote haben.

Wir differenzieren die Funktion und untersuchen dann die Wachstums- und Abnahmeintervalle:

$f(x)=\cfrac{x^2+2}{x^2-1} \ \longrightarrow \ f'(x)= \cfrac{2x \cdot (x^2-1) -(x^2+2) \cdot 2x}{\left(x^2-1 \right)^2}$

$f'(x)= \cfrac{2x^3-2x - (2x^3+4x) }{\left(x^2-1 \right)^2} = \cfrac{-6x}{\left(x^2-1 \right)^2}$

Nun setzen wir die Ableitung gleich 0 und lösen die Gleichung:

$f'(x)= 0$

$\cfrac{-6x}{\left(x^2-1 \right)^2}=0$

$-6x=0\cdot\left(x^2-1 \right)^2$

$-6x= 0$

$x=\cfrac{0}{-6} = 0$

Wir stellen auf der Linie alle berechneten kritischen Punkte dar, das sind die Punkte, die nicht zum Bereich gehören (x=-1 und x=+1) und diejenigen, die die Ableitung aufheben (x=0):

Und wir bewerten das Vorzeichen der Ableitung in jedem Intervall, um zu wissen, ob die Funktion zunimmt oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals die singulären Punkte) und schauen uns an, welches Vorzeichen die Ableitung an dieser Stelle hat:

$f'(-2)= \cfrac{-6(-2)}{\left((-2)^2-1 \right)^2} = \cfrac{12}{9} =1,33 \ \rightarrow \ \bm{+}$

$f'(-0,5)= \cfrac{-6(-0,5)}{\left((-0,5)^2-1 \right)^2} = \cfrac{3}{0,56} =5,33 \ \rightarrow \ \bm{+}$

$f'(0,5)= \cfrac{-6\cdot 0,5}{\left(0,5^2-1 \right)^2} = \cfrac{-3}{0,56} =-5,33 \ \rightarrow \ \bm{-}$

$f'(2)= \cfrac{-6\cdot 2}{\left(2^2-1 \right)^2} = \cfrac{-12}{9} =-1,33 \ \rightarrow \ \bm{-}$

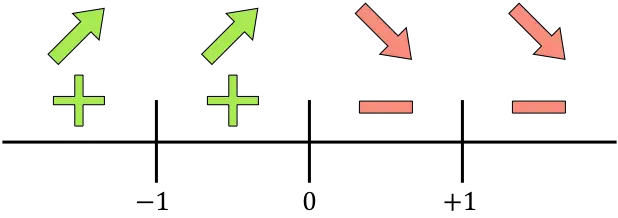
Die Funktion nimmt zu, wenn die Ableitung positiv ist, und die Funktion nimmt ab, wenn die Funktion negativ ist:

Wachstum:

$\bm{(-\infty,-1)\cup (-1,0)}$

Verringern:

$\bm{(0,1)\cup (1,+\infty)}$

Die Funktion geht bei x=0 vom Ansteigenden zum Absteigenden über, sodass x=0 ein lokales Maximum der Funktion ist.

Wir setzen das gefundene Extremum in die ursprüngliche Funktion ein, um die Y-Koordinate des Punktes zu ermitteln:

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2 \ \longrightarrow \ (0,-2)$

Die relativen Extremwerte der Funktion sind daher:

Maximal auf den Punkt gebracht

$\bm{(0,-2)}$

Um die Krümmung der Funktion zu untersuchen, berechnen wir ihre zweite Ableitung:

$f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}“ title=“Rendered by QuickLaTeX.com“> <p class=$ Alle Begriffe haben

$(x^2-1)$

, wir können daher den Bruch vereinfachen:

$f''(x)= \cfrac{-6 \left(x^2-1 \right)^{\cancel{2}} + 24x^2\cancel{(x^2-1)}}{\left(x^2-1 \right)^\cancelto{3}{4}} =\cfrac{-6 \left(x^2-1 \right) + 24x^2}{\left(x^2 -1\right)^3}$

$f''(x)= \cfrac{-6x^2+6 + 24x^2}{\left(x^2 -1\right)^3} =\cfrac{18x^2+6}{\left(x^2 -1\right)^3}$

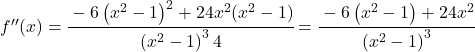
Nun setzen wir die zweite Ableitung gleich 0 und lösen die Gleichung:

$f''(x)= 0$

$\cfrac{18x^2+6}{\left(x^2 -1\right)^3}=0$

$18x^2+6=0\cdot \left(x^2 -1\right)^3$

$18x^2+6= 0$

$18x^2=-6$

$x^2=\cfrac{-6}{18}$

$x^2=-0,33$

$x=\sqrt{-0,33} \quad \color{red}\bm{\times}$

Es gibt keine Quadratwurzel einer negativen Zahl. Es gibt also keinen passenden Punkt

$f''(x)=0$

Nun stellen wir auf der Geraden alle gefundenen singulären Punkte dar, d. h. die Punkte, die nicht zum Definitionsbereich gehören (x=-1 und x=+1) und diejenigen, die die zweite Ableitung aufheben (in diesem Fall gibt es keine). beliebig):

Und wir bewerten das Vorzeichen der zweiten Ableitung in jedem Intervall, um zu wissen, ob die Funktion konkav oder konvex ist. Wir nehmen daher in jedem Intervall einen Punkt (niemals die singulären Punkte) und schauen uns an, welches Vorzeichen die zweite Ableitung an dieser Stelle hat:

$f''(-2)=\cfrac{18(-2)^2+6}{\left((-2)^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

$f''(0)=\cfrac{18\cdot 0^2+6}{\left(0^2 -1\right)^3}= \cfrac{6}{-1} = -6 \ \rightarrow \ \bm{-}$

$f''(2)=\cfrac{18\cdot 2^2+6}{\left(2^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

Wenn die zweite Ableitung positiv ist, bedeutet dies, dass die Funktion konvex ist.

$(\bm{\cup})$

, und wenn die zweite Ableitung negativ ist, bedeutet dies, dass die Funktion konkav ist

$(\bm{\cap})$

. Die Konkavitäts- und Konvexitätsintervalle sind daher:

Konvex

$(\bm{\cup})$

$\bm{(-\infty, -1) \cup (1, +\infty)}$

Konkav

$(\bm{\cap})$

$\bm{(-1,1)}$

Obwohl es bei x=-1 und bei x=1 zu einer Krümmungsänderung kommt, handelt es sich hierbei jedoch nicht um Wendepunkte. Weil sie nicht zum Funktionsbereich gehören.

Und schließlich stellen wir die Funktion anhand aller durchgeführten Berechnungen grafisch dar:

Übung 3

Zeichnen Sie die folgende rationale Funktion in ein Diagramm:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Sehen Sie sich die Lösung an

Da es sich um eine rationale Funktion handelt, müssen wir den Nenner auf 0 setzen, um zu sehen, welche Zahlen nicht zum Definitionsbereich der Funktion gehören:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Um den Schnittpunkt mit der X-Achse zu finden, lösen wir

$f(x)= 0.$

Da die Funktion auf der X-Achse immer den Wert 0 hat:

$f(x)=0$

$\cfrac{x^3}{x^2-4}=0$

$x^3=0\cdot (x^2-4)$

$x^3=0$

$x=\sqrt[3]{0}=0$

Der Schnittpunkt mit der X-Achse ist also:

$\bm{(0,0)}$

Und um den Schnittpunkt mit der Y-Achse zu finden, berechnen wir

$f(0).$

Da x auf der Y-Achse immer 0 ist:

$f(0)=\cfrac{0^3}{0^2-4} = \cfrac{0}{-4} = 0$

Der Schnittpunkt mit der Y-Achse ist also:

$\bm{(0,0)}$

In diesem Fall fällt der Schnittpunkt mit der X-Achse mit dem Schnittpunkt mit der Y-Achse zusammen, da die Funktion durch den Koordinatenursprung verläuft.

Um zu sehen, ob die Funktion vertikale Asymptoten hat, müssen wir den Grenzwert der Funktion an Punkten berechnen, die nicht zum Definitionsbereich gehören (in diesem Fall x=-2 und x=+2). Und wenn das Ergebnis unendlich ist, ist es eine vertikale Asymptote. Noch:

$\displaystyle \lim_{x \to -2} \cfrac{x^3}{x^2-4} = \cfrac{(-2)^3}{(-2)^2-4} =\cfrac{-8}{4-4}= \cfrac{-8}{0} = \infty$

Da der Grenzwert der Funktion, wenn x sich -2 nähert, Unendlich ergibt, ist x=-2 eine vertikale Asymptote.

Wir berechnen die seitlichen Grenzen der Asymptote x=-2, indem wir eine Zahl sehr nahe bei ihr in die Funktion einsetzen:

$\displaystyle f(-2,1)=\cfrac{(-2,1)^3}{(-2,1)^2-4} =-22,59 \longrightarrow \lim_{x \to -2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(-1,9)=\cfrac{(-1,9)^3}{(-1,9)^2-4} =+17,59 \longrightarrow \lim_{x \to -2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

Sehen wir uns nun an, ob x=+2 eine vertikale Asymptote ist:

$\displaystyle \lim_{x \to +2} \cfrac{x^3}{x^2-4} = \cfrac{(2)^3}{(2)^2-4} =\cfrac{8}{4-4}= \cfrac{8}{0} = \infty$

Da der Grenzwert der Funktion, wenn x sich +2 nähert, Unendlich ergibt, ist x=+2 eine vertikale Asymptote.

Wir berechnen die seitlichen Grenzen der Asymptote x=2, indem wir eine Zahl, die ihr sehr nahe kommt, in die Funktion einsetzen:

$\displaystyle f(1,9)=\cfrac{1,9^3}{1,9^2-4} =-17,59 \longrightarrow \lim_{x \to 2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(2,1)=\cfrac{2,1^3}{2,1^2-4} =22,59 \longrightarrow \lim_{x \to 2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

Andererseits ist die horizontale Asymptote der Funktion das Ergebnis der unendlichen Grenze der Funktion. Noch:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^3}{x^2-4} = \cfrac{+\infty}{+\infty } =+\infty$

Der unendliche Grenzwert der Funktion gab uns +∞, daher hat die Funktion keine horizontale Asymptote.

Wir berechnen nun die schräge Asymptote. Die schrägen Asymptoten haben die Form

$y=mx+n.$

UND

$m$

Die Berechnung erfolgt nach folgender Formel:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: x =\lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: \frac{x}{1}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3\cdot 1}{(x^2-4)\cdot x} =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x} = \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Sobald wir die Steigung der schrägen Asymptote kennen, bestimmen wir den Achsenabschnitt mithilfe der folgenden Formel:

$\displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]$

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Aber wir erhalten die Unbestimmtheit ∞ – ∞. Daher ist es notwendig, die Begriffe auf einen gemeinsamen Nenner zu bringen. Dazu multiplizieren und dividieren wir x durch den Nenner des Bruchs:

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]$

$\displaystyle n = \lim_{x \to +\infty} \cfrac{x^3- (x^3-4x)}{x^2-4} = \lim_{x \to +\infty} \cfrac{4x}{x^2-4}$

$\displaystyle n =\lim_{x \to +\infty} \cfrac{4x}{x^2-4} = \cfrac{+\infty}{\infty} =\bm{0}$

Kurz gesagt ist die schräge Asymptote:

$y = mx+n$

$y = 1x + 0$

$\bm{y = x }$

Um die Monotonie der Funktion zu untersuchen, müssen wir zunächst ihre Ableitung berechnen:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Nun setzen wir die Ableitung gleich 0 und lösen die Gleichung:

$f'(x)= 0$

$\cfrac{x^4-12x^2}{\left(x^2-4\right)^2}=0$

$x^4-12x^2=0\cdot \left(x^2-4\right)^2$

$x^4-12x^2=0$

$x^2(x^2-12)=0$

$\displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}$

Wir stellen nun auf der Geraden alle gefundenen singulären Punkte dar, also die Punkte, die nicht zum Definitionsbereich gehören (x=-2 und x=+2) und diejenigen, die die Ableitung aufheben (x=0, x=- 3,46 und x= +3,46):

Und wir bewerten das Vorzeichen der Ableitung in jedem Intervall, um zu wissen, ob die Funktion zunimmt oder abnimmt. Wir nehmen daher in jedem Intervall einen Punkt (niemals die singulären Punkte) und schauen uns an, welches Vorzeichen die Ableitung an dieser Stelle hat:

$f'(-4)= \cfrac{(-4)^4-12(-4)^2}{\left((-4)^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

$f'(-3)= \cfrac{(-3)^4-12(-3)^2}{\left((-3)^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(-1)= \cfrac{(-1)^4-12(-1)^2}{\left((-1)^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(1)= \cfrac{1^4-12\cdot1^2}{\left(1^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(3)= \cfrac{3^4-12\cdot 3^2}{\left(3^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(4)= \cfrac{4^4-12\cdot 4^2}{\left(4^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

Wachstum:

$\bm{(-\infty,-3,46)\cup (3,46,+\infty)}$

Verringern:

$\bm{(-3,46,-2)\cup(-2,0)\cup (0,2) \cup (2,3,46)}$

Die Funktion geht bei x=-3,46 vom Ansteigenden zum Absteigenden über, sodass x=-3,46 ein Maximum der Funktion ist. Und die Funktion geht bei x=3,46 von abnehmend zu steigend über, sodass x=3,46 ein Minimum der Funktion ist.

Wir bestimmen die Y-Koordinaten der relativen Enden:

$f(-3,46)=\cfrac{(-3,46)^3}{(-3,46)^2-4} = \cfrac{-41,42}{7,97}=-5,20 \ \longrightarrow \ (-3,46,-5,20)$

$f(3,46)=\cfrac{3,46^3}{3,46^2-4} = \cfrac{41,42}{7,97}=5,20 \ \longrightarrow \ (3,46,5,20)$

Die relativen Extremwerte der Funktion sind daher:

Maximal auf den Punkt gebracht

$\bm{(-3,46,-5,20)}$

Minimum bis Punkt

$\bm{(3,46,5,20)}$

Um die Krümmung der Funktion zu untersuchen, berechnen wir die zweite Ableitung der Funktion:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Nun setzen wir die zweite Ableitung gleich 0 und lösen die Gleichung:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

$x(8x^2+96)=0$

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Es gibt keine Lösung, da es keine negative Wurzel einer reellen Zahl gibt.

Wir stellen nun auf der Geraden alle gefundenen singulären Punkte dar, also die Punkte, die nicht zum Definitionsbereich gehören (x=-2 und x=+2) und diejenigen, die die zweite Ableitung aufheben (x=0):

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot 1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Wenn die zweite Ableitung positiv ist, bedeutet dies, dass die Funktion konvex ist.

$(\bm{\cup})$

, und wenn die zweite Ableitung negativ ist, bedeutet dies, dass die Funktion konkav ist

$(\bm{\cap})$

. Die Konkavitäts- und Konvexitätsintervalle sind daher:

Konvex

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Konkav

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Obwohl sich die Krümmung bei x=-2 und x=+2 ändert, handelt es sich hierbei jedoch nicht um Wendepunkte. Weil x=-2 und x=+2 nicht zum Definitionsbereich der Funktion gehören. Andererseits gibt es bei x=0 eine Krümmungsänderung (die Funktion geht von konvex nach konkav) und das gehört zur Funktion, also ist x=0 ein Wendepunkt.

Wir ersetzen die gefundenen Wendepunkte in der ursprünglichen Funktion, um die andere Koordinate des Wendepunkts zu finden:

$f(0) = \cfrac{0^3}{0^2-4} = \cfrac{0}{-4} =0\ \longrightarrow \ (0,0)$

Die Wendepunkte der Funktion sind also:

Wendepunkte:

$\bm{(0,0)}$

Basierend auf allen von uns berechneten Informationen stellen wir schließlich die Funktion dar:

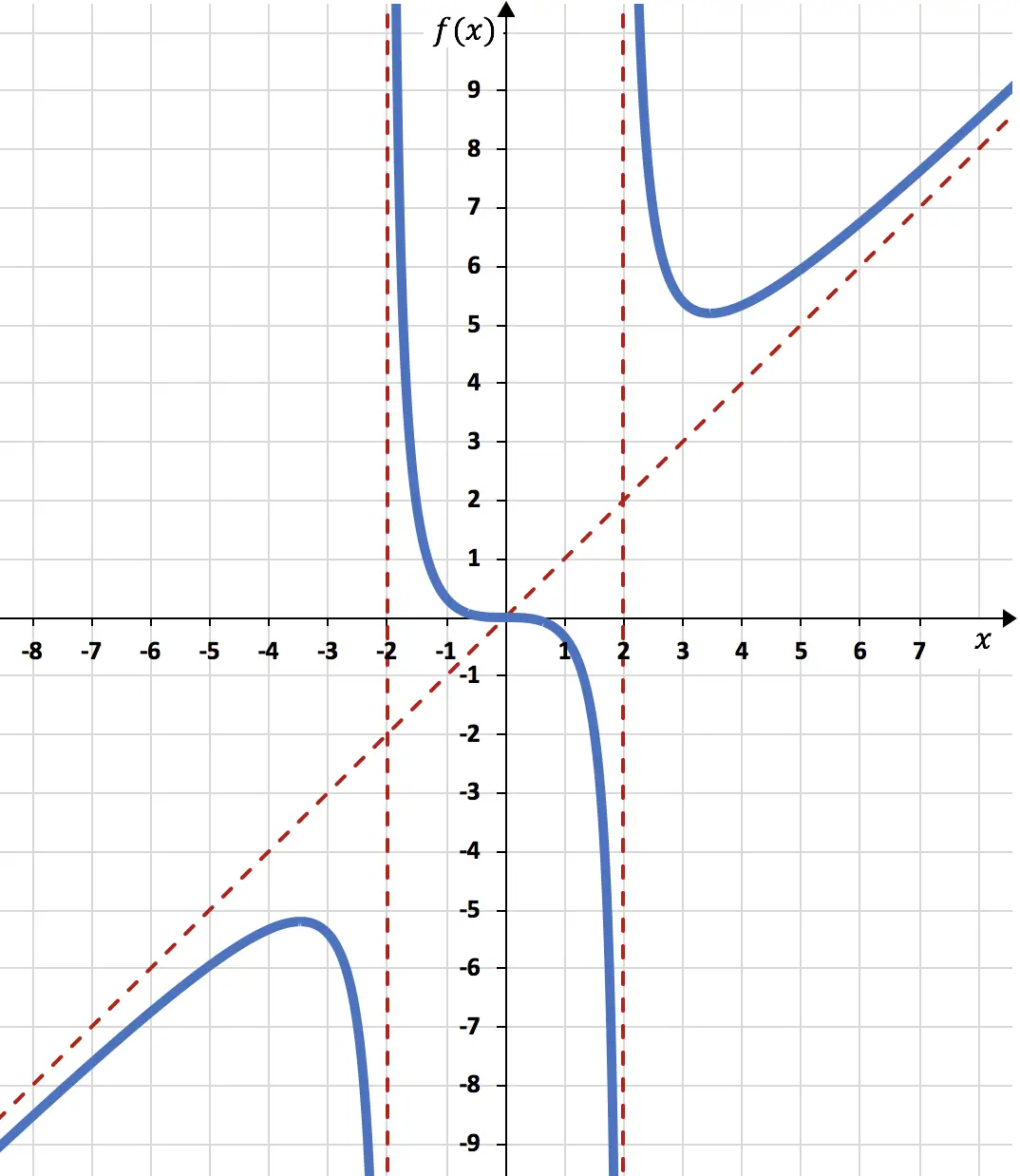
grafische Darstellung gelöster Funktionen, Übungen

Kommentar: Beachten Sie, dass die Funktion die schräge Asymptote an diesem Punkt schneidet

$(0,0) .$

Tatsächlich bestimmen die schrägen Asymptoten vor allem das Verhalten der Funktion, wenn x in Richtung +∞ und -∞ tendiert. Tatsächlich kreuzt die Funktion niemals die schräge Asymptote rechts vom Graphen (x→+∞) und links davon der Graph (x→-∞). Es kommt jedoch sehr selten vor, dass die Funktion die schräge Asymptote in der Mitte kreuzt, es handelt sich um einen ganz besonderen Fall.

Funktionsdarstellung

So stellen Sie eine Funktion in einem Diagramm dar

Beispiel für die Darstellung einer Funktion

Aufgaben zur Darstellung von Funktionen gelöst

Übung 1

Übung 2

Übung 3

Kommentar verfassen Kommentieren abbrechen