Carré d’une différence (ou soustraction)

Ici, nous expliquons ce qu’est la formule d’identité notable du carré d’une différence (ou soustraction), c’est-à-dire que nous vous montrons comment l’expression (ab) ² est résolue. De plus, vous pourrez voir des exemples et vous entraîner avec des exercices résolus sur le carré d’une différence. Et enfin, nous montrons la démonstration de la formule et l’interprétation géométrique de ce type de produit remarquable.

Quel est le carré d’une différence (ou d’une soustraction) ?

Le carré d’une différence , ou carré d’une soustraction , est l’une des identités notables (ou produits notables), c’est-à-dire qu’il consiste en une règle mathématique qui facilite le calcul de la quadrature d’un binôme à deux termes : l’un positif et l’autre négatif.

Par conséquent, l’expression algébrique du carré d’une différence est (ab) ² .

Formule du carré d’une différence (ou soustraction)

Une fois que nous aurons vu la définition de ce type d’identité remarquable, nous allons voir comment résoudre le carré d’une différence avec sa formule :

De sorte que le carré d’une différence est égal au carré du premier terme, moins le double du produit du premier par le second, plus le carré du second.

Donc, pour calculer une différence ou une soustraction au carré, il faut non seulement élever chaque terme à deux, mais aussi les multiplier entre eux et par 2.

Il est important de s’en souvenir, car une erreur très courante lors de la soustraction des carrés est de ne pas mettre le produit entre les deux termes et de ne résoudre que le carré de la diminution et la soustraction de la soustraction :

N’oubliez pas le produit entre a et b !

Exemples de carrés de différence (ou de soustraction)

Maintenant que nous connaissons la formule du carré d’une différence, nous pouvons faire des calculs avec. Et pour que vous puissiez voir comment cela se fait, nous avons préparé plusieurs exemples résolus du carré d’une différence (ou soustraction).

Exemple 1

• Résolvez la différence suivante élevée au carré :

C’est une soustraction au carré, il faut donc appliquer sa formule :

Donc, il faut identifier quelles sont les valeurs des inconnues

et de la formule. Dans ce cas, est la variable et correspond au numéro 3 :

Notez que le signe négatif ne fait pas partie de

mais il faut toujours prendre le nombre sans le signe pour appliquer correctement la formule.

Nous connaissons donc déjà les valeurs de

et de Par conséquent, nous n’avons qu’à substituer ces valeurs dans la formule :

Exemple 2

• Calculer le binôme suivant d’une soustraction élevée au carré :

La formule de la différence au carré est :

Donc, nous devons d’abord identifier les valeurs de

et de de la formule. Dans ce problème, représente le monôme et est équivalent au terme indépendant du binôme, soit 2 :

Enfin, une fois que nous connaissons la valeur des paramètres

et , on applique simplement la formule du binôme d’une soustraction élevée au carré :

Preuve de la formule du carré d’une différence

Nous allons ensuite déduire d’où vient la formule du carré d’une soustraction. Bien que vous n’ayez pas à mémoriser la preuve, il est toujours agréable de comprendre les mathématiques qui la sous-tendent.

Si l’on part de l’expression du binôme de toute soustraction :

Évidemment, la puissance précédente est égale au produit du facteur

multiplié par lui-même :

Maintenant, nous multiplions les deux parenthèses en appliquant la propriété distributive :

Et nous n’avons qu’à regrouper les termes similaires pour finir de démontrer la formule :

Pour que la formule du carré d’une soustraction soit mathématiquement prouvée :

Par curiosité, le développement de l’expression du binôme d’une soustraction au carré est également connu sous le nom de trinôme carré parfait.

Interprétation géométrique du carré d’une différence

Pour finir de comprendre la notion de carré d’une différence, nous allons voir comment interpréter géométriquement cette remarquable égalité.

Regardez le carré suivant avec des côtés de longueur

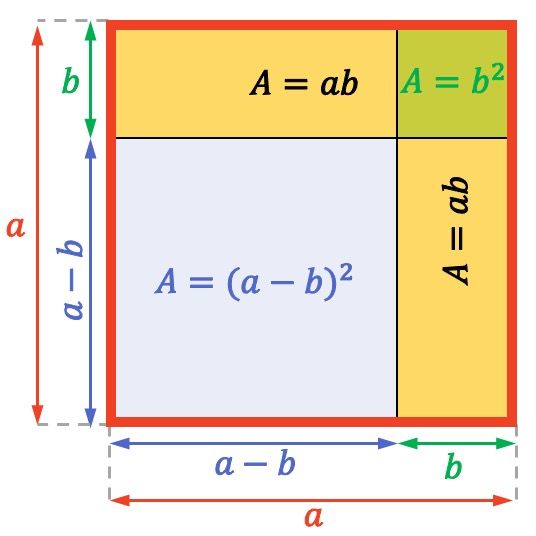
L’aire (ou surface) d’un carré ou d’un rectangle se calcule en multipliant deux de ses côtés adjacents. Par conséquent, l’aire du carré entier entier ci-dessus est

De même, l’aire de chaque rectangle jaune est égale à Et enfin, le petit carré représenté en haut à droite a une superficie de

Cela signifie qu’un carré de côté

dont la surface est peut être décomposé en l’aire d’un carré de dimension moins 2 fois l’aire d’un rectangle de dimensions et , plus l’aire d’un carré de côté En bref, la formule du carré d’une différence peut également être vérifiée géométriquement :

Problèmes résolus du carré d’une différence (ou soustraction)

Afin que vous puissiez vous entraîner, nous vous laissons avec plusieurs exercices résolus pas à pas sur le produit notable du carré d’une différence. N’oubliez pas que vous pouvez nous écrire toutes les questions que vous avez ci-dessous dans les commentaires.

Exercice 1

Résolvez les soustractions suivantes élevées au carré :

Pour trouver toutes les identités remarquables du problème, il suffit d’appliquer la formule du carré d’une différence, qui est :

Exercice 2

Déterminer les carrés suivants des différences de deux quantités en appliquant la formule :

Pour déterminer tous les produits notables du problème il faut utiliser la formule d’une soustraction élevée au carré :

Pour résoudre la section B), vous devez vous rappeler que si une racine est élevée au carré, elle est simplifiée :

Les monômes de la dernière soustraction au carré ont des coefficients fractionnaires, donc pour le résoudre, nous devons utiliser les propriétés des fractions :