Fonction rationnelle : qu'est-ce que c'est, domaine, asymptotes, graphique, exercices,...

Vous découvrirez ici ce que sont les fonctions rationnelles. De plus, nous expliquons comment calculer le domaine et les asymptotes d’une fonction rationnelle. Et pas seulement cela, mais vous verrez quelles sont toutes les caractéristiques des fonctions rationnelles. Enfin, vous pouvez vous entraîner avec des exercices étape par étape sur les fonctions rationnelles.

Qu’est-ce qu’une fonction rationnelle ?

La définition d’une fonction rationnelle est la suivante :

Une fonction rationnelle est une fonction formée par le quotient de deux polynômes , c’est-à-dire qu’une fonction rationnelle est une fraction qui a un polynôme au numérateur et au dénominateur.

Les fonctions rationnelles se caractérisent par des singularités aux points où le dénominateur s’annule.

$f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}$

Les fonctions rationnelles sont également appelées fonctions fractionnaires.

En revanche, les fonctions rationnelles ne doivent pas être confondues avec les fonctions irrationnelles. Les fonctions irrationnelles (ou radicales) sont celles qui sont constituées de racines.

Exemples de fonctions rationnelles

Pour mieux comprendre la notion de fonction rationnelle, nous allons voir plusieurs exemples de ce type de fonction.

Fonction rationnelle avec un polynôme du premier degré au numérateur et au dénominateur :

$f(x)=\cfrac{x+3}{2x-5}$

Ces types de fonctions rationnelles sont également appelées fonctions homographes .

Fonction rationnelle avec une constante au numérateur et un polynôme au dénominateur :

$f(x)=\cfrac{7}{x+1}$

Ces types de fonctions rationnelles sont appelés fonctions de proportionnalité inverse et sont utilisés pour définir mathématiquement des grandeurs inversement proportionnelles.

Fonction rationnelle avec un polynôme du troisième degré au numérateur et un polynôme du deuxième degré au dénominateur :

$f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}$

Domaine d’une fonction rationnelle

Un nombre divisé par 0 est une indétermination qui donne l’infini (∞), donc une fonction rationnelle existera toujours à moins que le dénominateur ne soit 0.

Par conséquent, le domaine d’une fonction rationnelle est constitué de tous les nombres réels à l’exception des valeurs qui annulent le dénominateur.

Donc, pour obtenir le domaine d’une fonction rationnelle, nous devons trouver lorsque le dénominateur est 0, puisque ce point sera le seul qui n’appartient pas au domaine

Voyons comment le domaine d’une fonction rationnelle est calculé en résolvant un exemple :

$f(x)=\cfrac{5x}{x+2}$

Nous fixons d’abord le dénominateur égal à 0, puis nous résolvons l’équation résultante :

$x+2=0$

$x=-2$

Par conséquent, lorsque x vaut -2, le dénominateur sera 0 et, par conséquent, la fonction n’existera pas. Le domaine de la fonction est donc constitué de tous les nombres réels sauf x=-2. Ceci est indiqué comme suit :

$\text{Dom } f= \mathbb{R}-\{ -2 \}$

Asymptotes d’une fonction rationnelle

L’une des principales propriétés des fonctions rationnelles sont leurs asymptotes, puisqu’elles déterminent leur représentation graphique.

➤ Voir : représentation graphique d’une fonction

Les asymptotes d’une fonction rationnelle sont des lignes dont le graphe de la fonction s’approche indéfiniment mais ne les touche jamais.

Il existe trois types d’asymptotes : les asymptotes verticales, les asymptotes horizontales et les asymptotes obliques.

Ci-dessous, vous avez les trois types d’asymptotes qu’une fonction rationnelle peut avoir représentée graphiquement en rouge.

Asymptote verticale d’une fonction rationnelle

Asymptote horizontale d’une fonction rationnelle

Asymptote oblique d’une fonction rationnelle

Comme vous pouvez le constater, déterminer l’asymptote d’une fonction à partir de son graphique est assez simple, mais calculer les asymptotes d’une fonction rationnelle sans avoir sa représentation graphique est assez compliqué. C’est pourquoi nous vous recommandons de voir comment sont calculées les asymptotes d’une fonction sur notre site Internet.

Caractéristiques d’une fonction rationnelle

Les fonctions rationnelles ont les caractéristiques suivantes :

$f(x)=\cfrac{P(x)}{Q(x)}$

Comme nous l’avons vu ci-dessus, le domaine des fonctions rationnelles comprend tous les nombres réels à l’exception des valeurs qui annulent le dénominateur de la fraction.

En général, la plage (ou plage) d’une fonction rationnelle comprend tous les nombres réels à l’exception des valeurs dans lesquelles la fonction a une asymptote horizontale.

Les fonctions rationnelles sont continues dans tout leur domaine. Ou en d’autres termes, les fonctions rationnelles présentent des discontinuités en des points qui n’appartiennent pas à leur domaine.

La représentation graphique de la plupart des fonctions rationnelles est constituée de deux hyperboles.

Certaines règles pour les asymptotes des fonctions rationnelles peuvent être déduites du polynôme numérateur. $P(x)$ et le polynôme dénominateur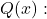
- Une fonction rationnelle a une asymptote verticale aux points qui sont les racines de $Q(x)$ mais ce ne sont pas des racines de $P(x).$
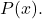
- Si le degré de $P(x)$ est inférieur au degré de $Q(x)$ , la droite y=0 est une asymptote horizontale de la fonction rationnelle.
- Si le degré de $P(x)$ est supérieur au degré de $Q(x)$ , la fonction rationnelle n’a pas d’asymptote horizontale.
- Si le degré de $P(x)$ est une unité supérieure au degré de $Q(x)$ et les deux polynômes n’ont pas de racine commune, la fonction rationnelle a une asymptote oblique.

Exercices résolus sur les fonctions rationnelles

Exercice 1

Trouvez le domaine de la fonction rationnelle suivante :

$f(x)=\displaystyle\frac{4x}{2x+4}$

Voir la solution

C’est une fonction rationnelle, donc le domaine est constitué de tous les nombres sauf ceux qui annulent le dénominateur, car alors la fonction donnerait ∞.

Nous mettons donc le dénominateur entier égal à zéro pour voir quel nombre n’appartient pas au domaine :

$2x+4=0$

Et on résout l’équation résultante :

$2x=-4$

$x=\cfrac{-4}{2}=-2$

Le domaine de la fonction est donc composé uniquement de nombres sauf -2 :

$\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }$

Exercice 2

Trouvez les points de coupure de la fonction rationnelle suivante avec les axes cartésiens :

$f(x)=\cfrac{x^2-9}{x}$

Voir la solution

Point de coupe avec l’axe X

Pour trouver le point d’intersection de la fonction avec l’axe X il faut résoudre

$f(x)=0:$

$f(x)=0$

$\cfrac{x^2-9}{x}=0$

$x^2-9=0\cdot x$

$x^2-9=0$

$x^2=9$

$x^2=\pm 3$

Nous avons obtenu deux solutions de l’équation du deuxième degré, donc la fonction rationnelle coupe l’axe des abscisses en deux points différents, qui sont :

$\bm{(3,0)\qquad (-3,0)}$

Point de coupe avec l’axe Y

Pour trouver le point d’intersection avec l’axe Y il faut calculer

$f(0):$

$f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty$

Tout nombre divisé par zéro est une indétermination qui donne l’infini. Par conséquent, la fonction rationnelle ne passe en aucun point au-dessus de l’axe Y, c’est-à-dire qu’elle n’a aucun point d’intersection avec l’axe des ordonnées.

Exercice 3

Représentez la fonction rationnelle suivante sur un graphique :

$y=\cfrac{2x+3}{2x+6}$

Voir la solution

La première chose à faire est de calculer le domaine de la fonction :

$2x+6=0$

$2x =-6$

$x =\cfrac{-6}{2} =-3$

$\text{Dom } f = \mathbb{R} - \{ -3 \}$

Une fois que l’on connaît le domaine de la fonction, on construit une table de valeurs :

$\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}$

Pour finir, il suffit de représenter les points obtenus sur un graphique et de tracer les hyperboles, dessinant ainsi la fonction rationnelle :

Exercice 4

Déterminez les asymptotes de la fonction rationnelle représentée graphiquement ci-dessous :

Voir la solution

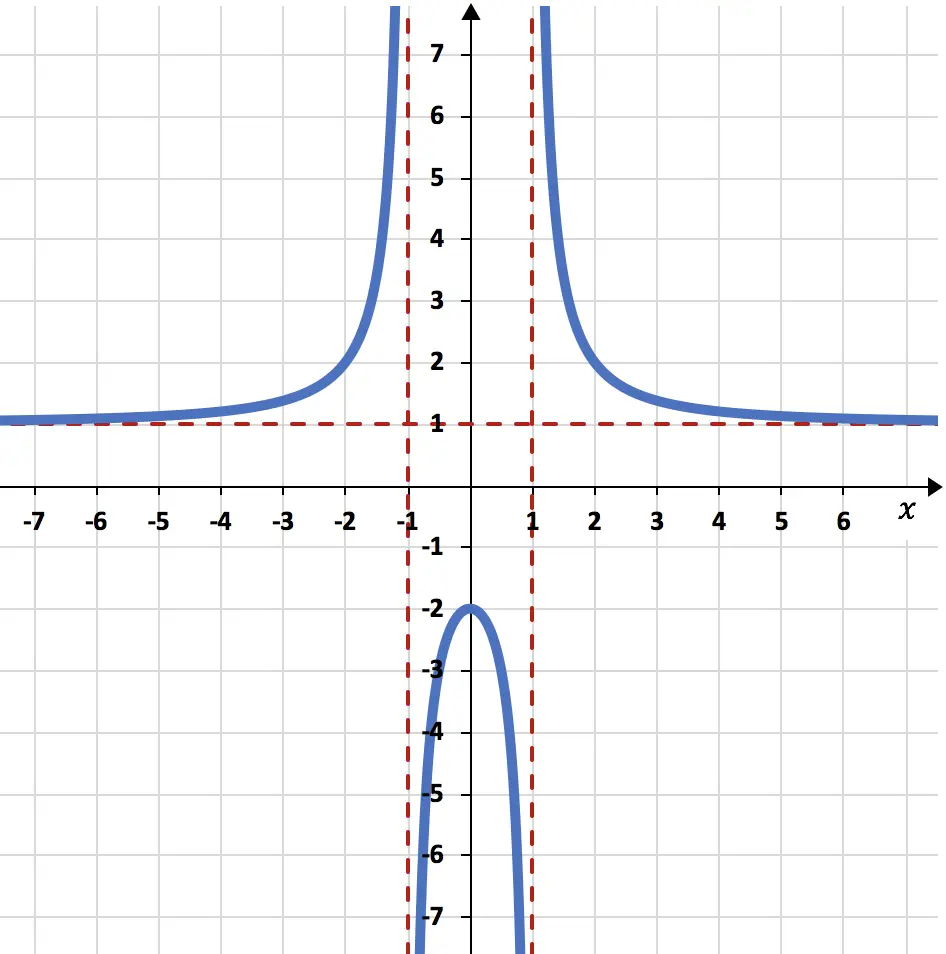
Les asymptotes sont très bien visibles sur le graphique, puisqu’elles sont représentées sous forme de lignes pointillées rouges.

Dans ce problème, la fonction est très proche de la ligne horizontale y=1 mais ne la touche jamais. Par conséquent, la fonction rationnelle a une seule asymptote horizontale, qui est y=1.

De même, la représentation graphique de la fonction est très proche des lignes verticales x=-1 et x=1, mais n’atteint jamais ces valeurs. La fonction rationnelle a donc deux asymptotes verticales différentes, qui sont x=-1 et x=1.

Exercice 5

Calculez toutes les asymptotes de la fonction rationnelle suivante :

$\displaystyle f(x)=\frac{6x-4}{2x+2}$

Remarque : pour résoudre cet exercice, nous vous recommandons d’aller d’abord sur le lien ci-dessus sur la façon dont les asymptotes d’une fonction sont calculées et de voir l’explication.

Voir la solution

asymptote verticale

Pour calculer les asymptotes verticales d’une fonction, il faut d’abord trouver le domaine de la fonction. Par conséquent, nous fixons le dénominateur de la fonction rationnelle égal à 0 pour trouver les points qui n’appartiennent pas au domaine :

$2x +2 =0$

$2x= -2$

$x = \cfrac{-2}{2} = -1$

Le domaine de la fonction est donc constitué de tous les nombres sauf -1 :

$\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}$

Donc x=-1 pourrait être une asymptote verticale. Pour vérifier cela, il faut calculer la limite de la fonction au point :

$\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty$

Par conséquent, x=-1 est une asymptote verticale de la fonction rationnelle, puisque la limite de la fonction en ce point donne l’infini.

asymptote horizontale

Pour déterminer les asymptotes horizontales, nous devons calculer la limite infinie de la fonction :

$\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}$

$\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}$

Dans ce cas, le résultat de la limite infinie indéterminée entre l’infini est la division des coefficients des x du plus haut degré, puisque le numérateur et le dénominateur sont du même ordre.

Les deux limites infinies de la fonction nous ont donné 3, donc y=3 est une asymptote horizontale de la fonction rationnelle.

asymptote oblique

Puisqu’il existe une asymptote horizontale, la fonction rationnelle n’a pas d’asymptote oblique.

Qu’est-ce qu’une fonction rationnelle ?

Exemples de fonctions rationnelles

Domaine d’une fonction rationnelle

Asymptotes d’une fonction rationnelle

Caractéristiques d’une fonction rationnelle

Exercices résolus sur les fonctions rationnelles

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Leave a Comment Cancel Reply